R'de spline regresyon nasıl gerçekleştirilir (örnekle)

Spline regresyon, verilerdeki desenin aniden değiştiği noktalar veya “düğümler” olduğunda ve doğrusal regresyon ile polinom regresyonun verilere uyacak kadar esnek olmadığı durumlarda kullanılan bir regresyon türüdür.

Aşağıdaki adım adım örnek, R’de spline regresyonunun nasıl gerçekleştirileceğini gösterir.

1. Adım: Verileri oluşturun

Öncelikle R’de iki değişkenli bir veri seti oluşturalım ve değişkenler arasındaki ilişkiyi görselleştirmek için bir dağılım grafiği oluşturalım:

 #create data frame
df <- data. frame (x=1:20,
                 y=c(2, 4, 7, 9, 13, 15, 19, 16, 13, 10,
                     11, 14, 15, 15, 16, 15, 17, 19, 18, 20))

#view head of data frame
head(df)

  xy
1 1 2
2 2 4
3 3 7
4 4 9
5 5 13
6 6 15

#create scatterplot
plot(df$x, df$y, cex= 1.5 , pch= 19 )

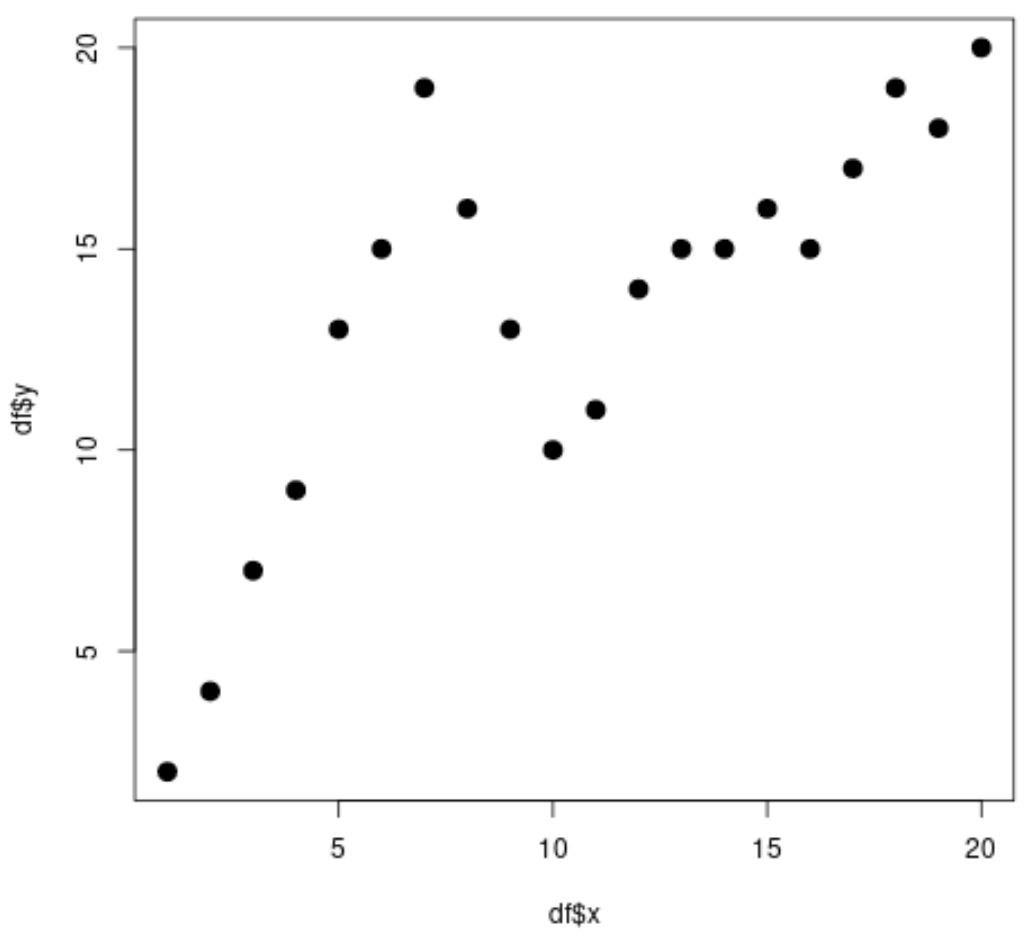
Açıkçası, x ve y arasındaki ilişki doğrusal değildir ve verideki modelin x=7 ve x=10’da aniden değiştiği iki nokta veya “düğüm” var gibi görünmektedir.

Adım 2: Basit doğrusal regresyon modelini yerleştirin

Daha sonra bu veri setine basit bir doğrusal regresyon modeli sığdırmak için lm() fonksiyonunu kullanalım ve dağılım grafiğinde regresyon doğrusunu uygun şekilde çizelim:

 #fit simple linear regression model
linear_fit <- lm(df$y ~ df$x)

#view model summary
summary(linear_fit)

Call:
lm(formula = df$y ~ df$x)

Residuals:
    Min 1Q Median 3Q Max 
-5.2143 -1.6327 -0.3534 0.6117 7.8789 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 6.5632 1.4643 4.482 0.000288 ***
df$x 0.6511 0.1222 5.327 4.6e-05 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.152 on 18 degrees of freedom
Multiple R-squared: 0.6118, Adjusted R-squared: 0.5903 
F-statistic: 28.37 on 1 and 18 DF, p-value: 4.603e-05

#create scatterplot
plot(df$x, df$y, cex= 1.5 , pch= 19 )

#add regression line to scatterplot
abline(linear_fit) 

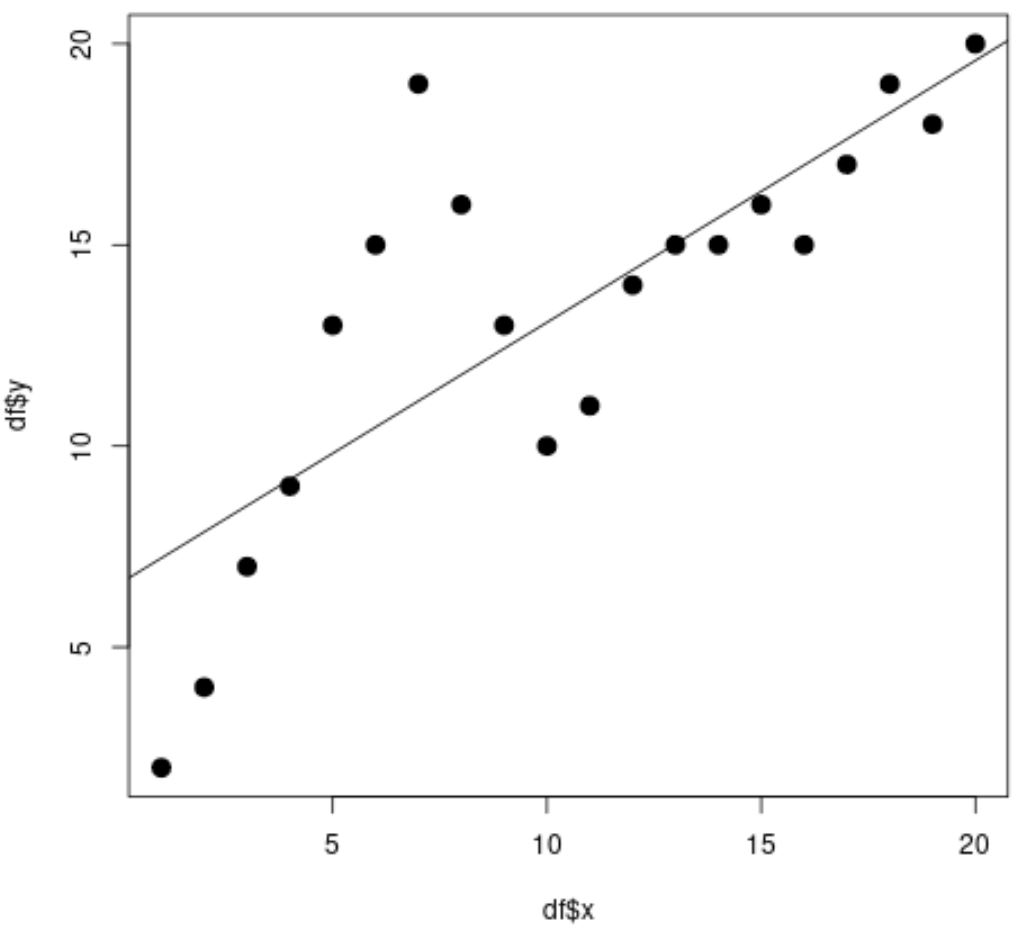
Dağılım grafiğinden basit doğrusal regresyon çizgisinin verilere iyi uymadığını görebiliriz.

Model sonuçlarından düzeltilmiş R-kare değerinin 0,5903 olduğunu da görebiliyoruz.

Bunu bir spline modelinin düzeltilmiş R-kare değeriyle karşılaştıracağız.

Adım 3: Spline regresyon modelini yerleştirin

Daha sonra, iki düğümlü bir spline regresyon modelini sığdırmak için splines paketindeki bs() işlevini kullanalım ve ardından takılan modeli dağılım grafiğinde çizelim:

 library (splines)

#fit spline regression model
spline_fit <- lm(df$y ~ bs(df$x, knots=c( 7 , 10 )))

#view summary of spline regression model
summary(spline_fit)

Call:
lm(formula = df$y ~ bs(df$x, knots = c(7, 10)))

Residuals:
     Min 1Q Median 3Q Max 
-2.84883 -0.94928 0.08675 0.78069 2.61073 

Coefficients:
                            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 2.073 1.451 1.429 0.175    
bs(df$x, knots = c(7, 10))1 2.173 3.247 0.669 0.514    
bs(df$x, knots = c(7, 10))2 19.737 2.205 8.949 3.63e-07 ***
bs(df$x, knots = c(7, 10))3 3.256 2.861 1.138 0.274    
bs(df$x, knots = c(7, 10))4 19.157 2.690 7.121 5.16e-06 ***
bs(df$x, knots = c(7, 10))5 16.771 1.999 8.391 7.83e-07 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.568 on 14 degrees of freedom
Multiple R-squared: 0.9253, Adjusted R-squared: 0.8987 
F-statistic: 34.7 on 5 and 14 DF, p-value: 2.081e-07

#calculate predictions using spline regression model
x_lim <- range(df$x)
x_grid <- seq(x_lim[ 1 ], x_lim[ 2 ])
preds <- predict(spline_fit, newdata=list(x=x_grid))

#create scatter plot with spline regression predictions
plot(df$x, df$y, cex= 1.5 , pch= 19 )
lines(x_grid, preds) 

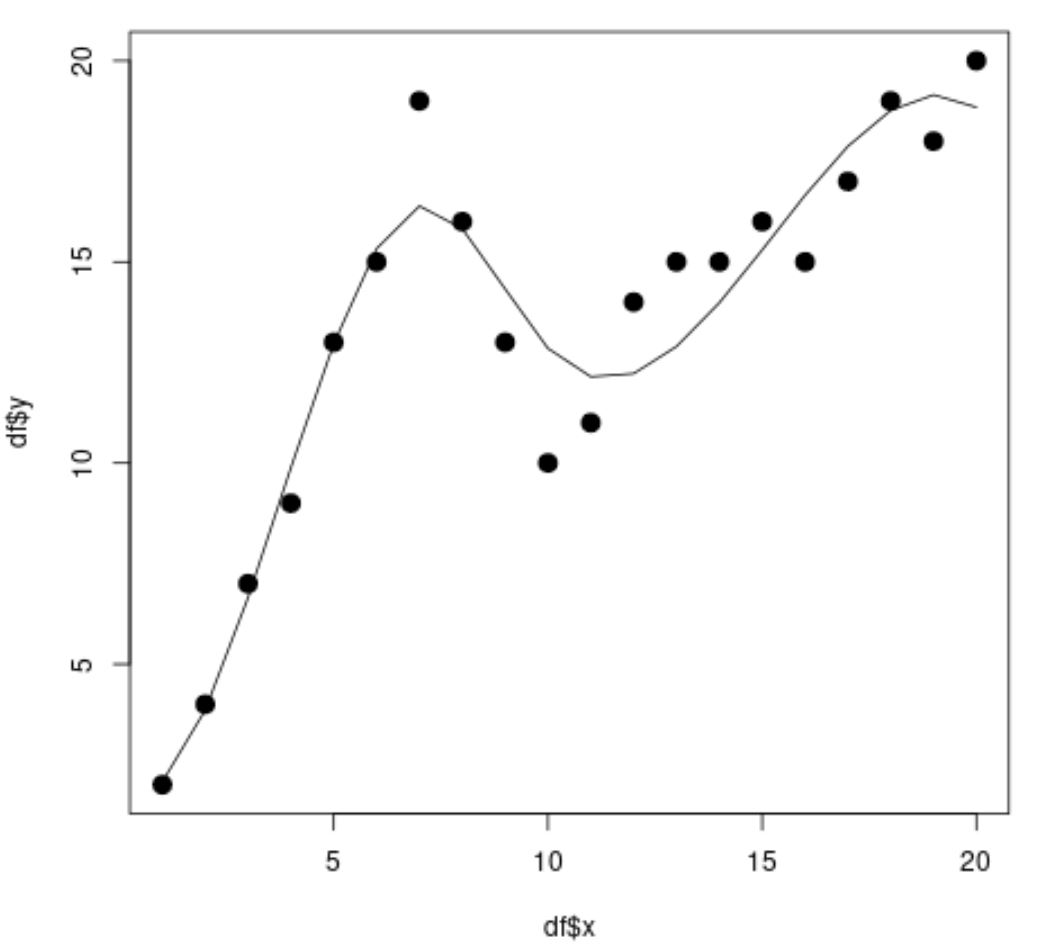
Dağılım grafiğinden spline regresyon modelinin verilere oldukça iyi uyum sağlayabildiğini görebiliriz.

Model sonuçlarından düzeltilmiş R-kare değerinin 0,8987 olduğunu da görebiliyoruz.

Bu model için düzeltilmiş R-kare değeri, basit doğrusal regresyon modelinden çok daha yüksektir, bu da bize spline regresyon modelinin verilere daha iyi uyum sağlayabildiğini söyler.

Bu örnekte düğümlerin x=7 ve x=10’da konumlandığını seçtiğimize dikkat edin.

Uygulamada, verilerdeki kalıpların değiştiği yere ve alan uzmanlığınıza bağlı olarak düğüm konumlarını kendiniz seçmeniz gerekecektir.

Ek kaynaklar

Aşağıdaki eğitimlerde R’de diğer ortak görevlerin nasıl gerçekleştirileceği açıklanmaktadır:

R’de çoklu doğrusal regresyon nasıl gerçekleştirilir
R’de üstel regresyon nasıl gerçekleştirilir
R’de ağırlıklı en küçük kareler regresyonu nasıl gerçekleştirilir?