R'de temel bileşen analizi: adım adım örnek

Çoğunlukla PCA olarak kısaltılan temel bileşenler analizi, bir veri kümesindeki varyasyonun büyük bir bölümünü açıklayan temel bileşenleri (orijinal tahmin edicilerin doğrusal kombinasyonları) bulmayı amaçlayan denetimsiz bir makine öğrenme tekniğidir.

PCA’nın amacı, bir veri setindeki değişkenliğin çoğunu orijinal veri setinden daha az değişkenle açıklamaktır.

p değişkenli belirli bir veri seti için, değişkenlerin her ikili kombinasyonunun dağılım grafiklerini inceleyebiliriz, ancak dağılım grafiklerinin sayısı çok hızlı bir şekilde artabilir.

p tahmincileri için p(p-1)/2 nokta bulutları mevcuttur.

Yani, p = 15 öngörücüye sahip bir veri kümesi için 105 farklı dağılım grafiği olacaktır!

Neyse ki PCA, verideki varyasyonun mümkün olduğu kadar çoğunu yakalayan bir veri kümesinin düşük boyutlu bir temsilini bulmanın bir yolunu sunuyor.

Eğer varyasyonun çoğunu sadece iki boyutta yakalayabilirsek, orijinal veri setindeki tüm gözlemleri basit bir dağılım grafiğine yansıtabiliriz.

Ana bileşenleri bulma şeklimiz şu şekildedir:

P _{tahmin ediciye sahip bir veri kümesi verildiğinde} : _

• _{Z m = ΣΦ jm _}
• Z ₁ , mümkün olduğu kadar çok varyansı yakalayan tahmin edicilerin doğrusal birleşimidir.
• _{Z2, Z1’e} dik (yani ilişkisiz) iken en fazla varyansı yakalayan tahmin edicilerin bir sonraki doğrusal kombinasyonudur.
• Bu durumda _{Z3, Z2’ye} dik iken en fazla varyansı yakalayan tahmin edicilerin bir sonraki doğrusal kombinasyonudur.
• Ve benzeri.

Uygulamada, orijinal tahmin edicilerin doğrusal kombinasyonlarını hesaplamak için aşağıdaki adımları kullanırız:

1. Değişkenlerin her birini ortalama 0 ve standart sapma 1 olacak şekilde ölçeklendirin.

2. Ölçeklenen değişkenler için kovaryans matrisini hesaplayın.

3. Kovaryans matrisinin özdeğerlerini hesaplayın.

Doğrusal cebir kullanarak, en büyük özdeğere karşılık gelen özvektörün ilk temel bileşen olduğunu gösterebiliriz. Başka bir deyişle, yordayıcıların bu özel kombinasyonu verilerdeki en büyük varyansı açıklamaktadır.

İkinci en büyük özdeğere karşılık gelen özvektör ikinci temel bileşendir ve bu şekilde devam eder.

Bu eğitimde, bu işlemin R’de nasıl gerçekleştirileceğine ilişkin adım adım bir örnek sunulmaktadır.

1. Adım: Verileri yükleyin

İlk önce verileri görselleştirmek ve işlemek için çeşitli yararlı işlevler içeren Tidyverse paketini yükleyeceğiz:

 library (tidyverse)

Bu örnek için, 1973’te ABD’nin her eyaletinde 100.000 kişi başına cinayet , saldırı ve tecavüz nedeniyle tutuklananların sayısını içeren, R’de yerleşik USArrests veri kümesini kullanacağız.

Aynı zamanda her eyaletin kentsel alanlarda yaşayan nüfusunun yüzdesini de içerir (UrbanPop) .

Aşağıdaki kod, veri kümesinin ilk satırlarının nasıl yüklenip görüntüleneceğini gösterir:

 #load data
data ("USArrests")

#view first six rows of data
head(USArrests)

           Murder Assault UrbanPop Rape
Alabama 13.2 236 58 21.2
Alaska 10.0 263 48 44.5
Arizona 8.1 294 80 31.0
Arkansas 8.8 190 50 19.5
California 9.0 276 91 40.6
Colorado 7.9 204 78 38.7

Adım 2: Temel bileşenleri hesaplayın

Verileri yükledikten sonra, veri kümesinin ana bileşenlerini hesaplamak için R’nin yerleşik fonksiyonu prcomp()’u kullanabiliriz.

Temel bileşenler hesaplanmadan önce veri kümesindeki değişkenlerin her birinin ortalaması 0 ve standart sapması 1 olacak şekilde ölçeklenmesi için ölçek = DOĞRU belirttiğinizden emin olun.

Ayrıca R’deki özvektörlerin varsayılan olarak negatif yönde olduğunu unutmayın; bu nedenle işaretleri tersine çevirmek için -1 ile çarpacağız.

 #calculate main components
results <- prcomp(USArrests, scale = TRUE )

#reverse the signs
results$rotation <- -1*results$rotation

#display main components
results$rotation

               PC1 PC2 PC3 PC4
Murder 0.5358995 -0.4181809 0.3412327 -0.64922780
Assault 0.5831836 -0.1879856 0.2681484 0.74340748
UrbanPop 0.2781909 0.8728062 0.3780158 -0.13387773
Rape 0.5434321 0.1673186 -0.8177779 -0.08902432

İlk temel bileşenin (PC1) cinayet, saldırı ve tecavüz için yüksek değerlere sahip olduğunu görebiliyoruz, bu da bu temel bileşenin bu değişkenlerdeki en büyük varyasyonu açıkladığını gösteriyor.

Ayrıca ikinci temel bileşenin (PC2) UrbanPop için yüksek bir değere sahip olduğunu görebiliriz, bu da bu temel bileşenin kentsel nüfusu vurguladığını gösterir.

Her durum için temel bileşen puanlarının results$x dosyasında saklandığını unutmayın. İşaretleri tersine çevirmek için bu puanları da -1 ile çarpacağız:

 #reverse the signs of the scores
results$x <- -1*results$x

#display the first six scores
head(results$x)

                  PC1 PC2 PC3 PC4
Alabama 0.9756604 -1.1220012 0.43980366 -0.154696581
Alaska 1.9305379 -1.0624269 -2.01950027 0.434175454
Arizona 1.7454429 0.7384595 -0.05423025 0.826264240
Arkansas -0.1399989 -1.1085423 -0.11342217 0.180973554
California 2.4986128 1.5274267 -0.59254100 0.338559240
Colorado 1.4993407 0.9776297 -1.08400162 -0.001450164

Adım 3: Sonuçları biplot ile görselleştirin

Daha sonra, veri kümesindeki gözlemlerin her birini eksen olarak birinci ve ikinci ana bileşenleri kullanan bir dağılım grafiğine yansıtan bir çizim olan bir çift nokta oluşturabiliriz:

Scale = 0 değerinin çizimdeki okların yüklemeleri temsil edecek şekilde ölçeklendirilmesini sağladığına dikkat edin.

 biplot(results, scale = 0 )

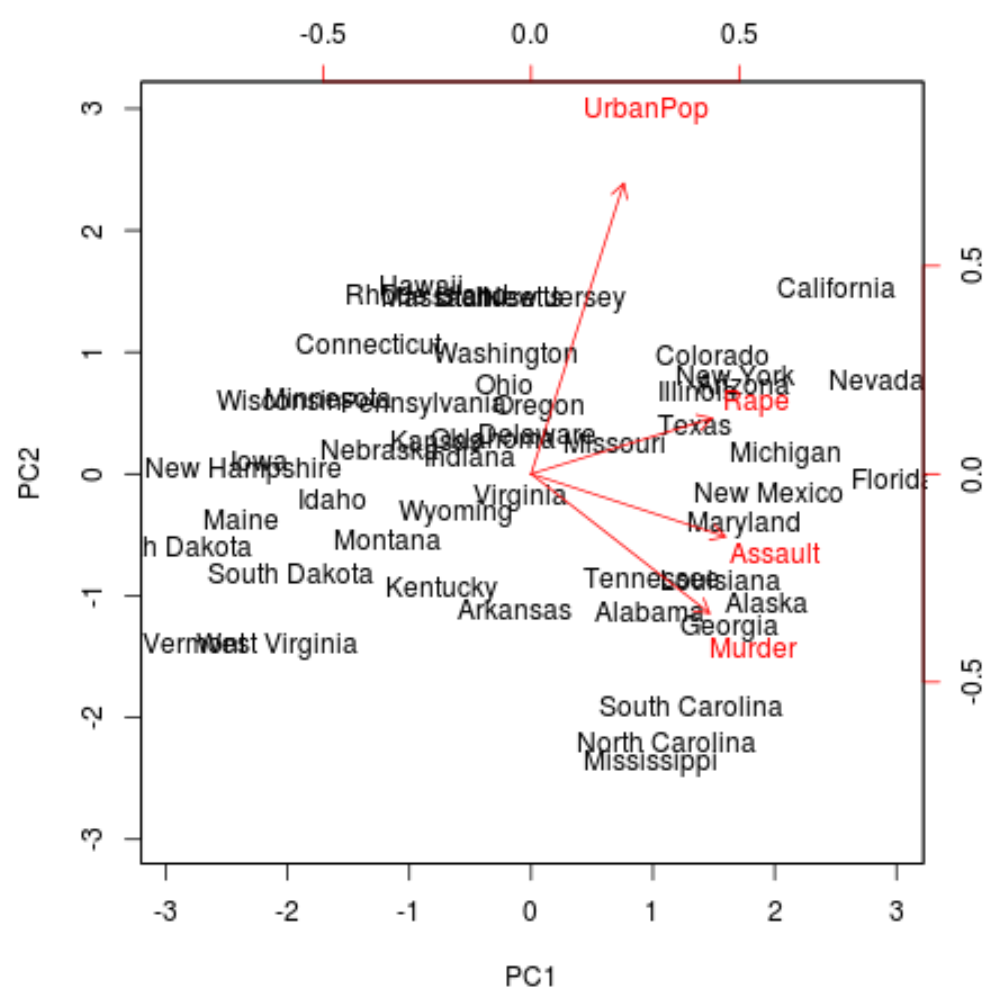
Çizimden, basit iki boyutlu bir uzayda temsil edilen 50 durumun her birini görebiliriz.

Grafikte birbirine yakın olan durumlar, orijinal veri kümesindeki değişkenlere göre benzer veri modellerine sahiptir.

Ayrıca bazı eyaletlerin belirli suçlarla diğerlerine göre daha güçlü bir şekilde ilişkilendirildiğini de görebiliriz. Örneğin olay örgüsünde Cinayet değişkenine en yakın eyalet Gürcistan’dır.

Orijinal veri setinde cinayet oranlarının en yüksek olduğu eyaletlere baktığımızda Gürcistan’ın listenin başında yer aldığını görebiliriz:

 #display states with highest murder rates in original dataset
head(USArrests[ order (-USArrests$Murder),])

               Murder Assault UrbanPop Rape
Georgia 17.4 211 60 25.8
Mississippi 16.1 259 44 17.1
Florida 15.4 335 80 31.9
Louisiana 15.4 249 66 22.2
South Carolina 14.4 279 48 22.5
Alabama 13.2 236 58 21.2

Adım 4: Her bir temel bileşenin açıkladığı varyansı bulun

Her bir temel bileşen tarafından açıklanan orijinal veri setindeki toplam varyansı hesaplamak için aşağıdaki kodu kullanabiliriz:

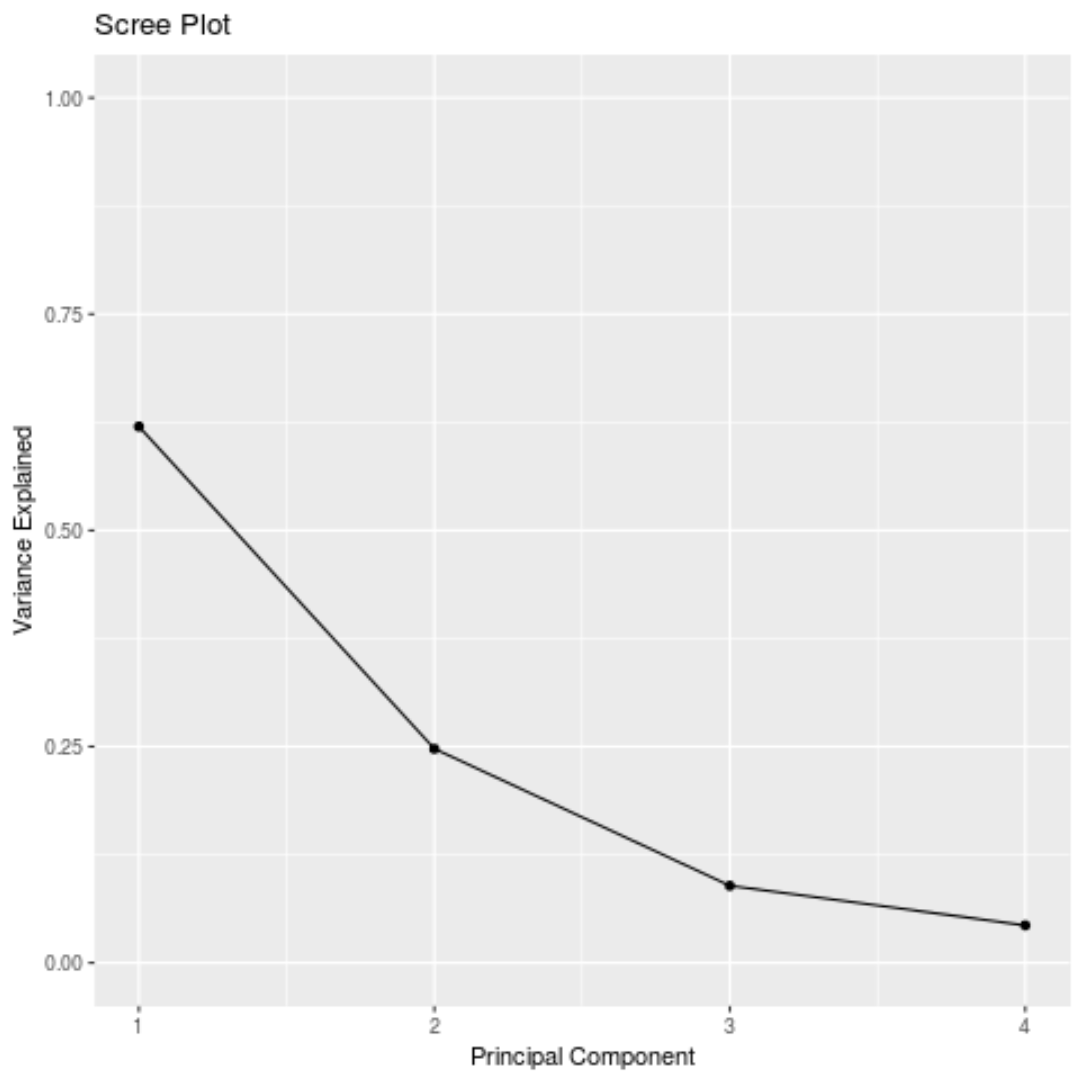
 #calculate total variance explained by each principal component
results$sdev^2 / sum (results$sdev^2)

[1] 0.62006039 0.24744129 0.08914080 0.04335752

Sonuçlardan şunları gözlemleyebiliriz:

• İlk temel bileşen, veri kümesindeki toplam varyansın %62’sini açıklamaktadır.
• İkinci temel bileşen veri setindeki toplam varyansın %24,7’sini açıklamaktadır.
• Üçüncü temel bileşen veri setindeki toplam varyansın %8,9’unu açıklamaktadır.
• Dördüncü temel bileşen veri setindeki toplam varyansın %4,3’ünü açıklamaktadır.

Dolayısıyla ilk iki temel bileşen verilerdeki toplam varyansın çoğunluğunu açıklamaktadır.

Bu iyi bir işaret çünkü önceki iki noktalı grafik, orijinal verilerdeki gözlemlerin her birini yalnızca ilk iki temel bileşeni hesaba katan bir dağılım grafiğine yansıtıyordu.

Bu nedenle, birbirine benzer durumları belirlemek için biplottaki kalıpları incelemek geçerlidir.

Ayrıca PCA sonuçlarını görselleştirmek için her bir ana bileşen tarafından açıklanan toplam varyansı gösteren bir grafik olan bir yamaç grafiği de oluşturabiliriz:

 #calculate total variance explained by each principal component
var_explained = results$sdev^2 / sum (results$sdev^2)

#create scree plot
qplot(c(1:4), var_explained) + 
  geom_line() + 
  xlab(" Principal Component ") + 
  ylab(" Variance Explained ") +
  ggtitle(" Scree Plot ") +
  ylim(0, 1) 

Uygulamada temel bileşen analizi

Uygulamada PCA en sık iki nedenden dolayı kullanılır:

1. Keşifsel Veri Analizi – Bir veri setini ilk kez araştırırken ve verilerdeki hangi gözlemlerin birbirine en çok benzediğini anlamak istediğimizde PCA’yı kullanırız.

2. Temel Bileşen Regresyonu – Daha sonra temel bileşen regresyonunda kullanılabilecek temel bileşenleri hesaplamak için PCA’yı da kullanabiliriz. Bu tür regresyon genellikle bir veri setindeki tahminciler arasında çoklu bağlantı olduğunda kullanılır.

Bu eğitimde kullanılan R kodunun tamamını burada bulabilirsiniz.