R'de ridge regresyon (adım adım)

Ridge regresyonu, verilerde çoklu bağlantı mevcut olduğunda regresyon modeline uyum sağlamak için kullanabileceğimiz bir yöntemdir.

Özetle, en küçük kareler regresyonu, kalan kareler toplamını (RSS) en aza indiren katsayı tahminlerini bulmaya çalışır:

RSS = Σ(y _ben – ŷ _ben )2

Altın:

• Σ : Toplam anlamına gelen bir Yunan sembolü
• y _i : ^i’inci gözlem için gerçek yanıt değeri
• ŷ _i : Çoklu doğrusal regresyon modeline dayalı olarak tahmin edilen yanıt değeri

Tersine, sırt regresyonu aşağıdakileri en aza indirmeyi amaçlar:

RSS + λΣβ _j ²

burada j 1’den p öngörücü değişkenlere gider ve λ ≥ 0’dır.

Denklemdeki bu ikinci terim çekilme cezası olarak bilinir. Sırt regresyonunda, λ için mümkün olan en düşük MSE testini (ortalama kare hatası) üreten bir değer seçeriz.

Bu eğitimde R’de ridge regresyonunun nasıl gerçekleştirileceğine ilişkin adım adım bir örnek sunulmaktadır.

1. Adım: Verileri yükleyin

Bu örnek için R’nin mtcars adı verilen yerleşik veri kümesini kullanacağız. Yanıt değişkeni olarak hp’yi ve yordayıcılar olarak aşağıdaki değişkenleri kullanacağız:

• mpg
• ağırlık
• bok
• qsec

Ridge regresyonunu gerçekleştirmek için glmnet paketindeki fonksiyonları kullanacağız. Bu paket, yanıt değişkeninin bir vektör olmasını ve tahmin değişkenleri kümesinin data.matrix sınıfından olmasını gerektirir.

Aşağıdaki kod verilerimizi nasıl tanımlayacağımızı gösterir:

 #define response variable
y <- mtcars$hp

#define matrix of predictor variables
x <- data.matrix(mtcars[, c('mpg', 'wt', 'drat', 'qsec')])

Adım 2: Ridge Regresyon Modelini Yerleştirin

Daha sonra, Ridge regresyon modeline uyum sağlamak için glmnet() işlevini kullanacağız ve alpha=0 değerini belirleyeceğiz.

Alfayı 1’e eşitlemenin Kement regresyonunu kullanmaya eşdeğer olduğunu ve alfayı 0 ile 1 arasında bir değere ayarlamanın elastik ağ kullanmaya eşdeğer olduğunu unutmayın.

Ayrıca, ridge regresyonunun, her öngörücü değişkenin ortalaması 0 ve standart sapması 1 olacak şekilde verilerin standartlaştırılmasını gerektirdiğini unutmayın.

Neyse ki glmnet() bu standardizasyonu sizin için otomatik olarak yapıyor. Değişkenleri zaten standartlaştırdıysanız standardize=False belirtebilirsiniz.

 library (glmnet)

#fit ridge regression model
model <- glmnet(x, y, alpha = 0 )

#view summary of model
summary(model)

          Length Class Mode   
a0 100 -none- numeric
beta 400 dgCMatrix S4     
df 100 -none- numeric
dim 2 -none- numeric
lambda 100 -none- numeric
dev.ratio 100 -none- numeric
nulldev 1 -none- numeric
npasses 1 -none- numeric
jerr 1 -none- numeric
offset 1 -none- logical
call 4 -none- call   
nobs 1 -none- numeric

3. Adım: Lambda için en uygun değeri seçin

Daha sonra, k-katlı çapraz doğrulamayı kullanarak en düşük test ortalama kare hatasını (MSE) üreten lambda değerini tanımlayacağız.

Neyse ki glmnet , k = 10 kez kullanılarak otomatik olarak k-katlı çapraz doğrulama gerçekleştiren cv.glmnet() işlevine sahiptir.

 #perform k-fold cross-validation to find optimal lambda value
cv_model <- cv. glmnet (x, y, alpha = 0 )

#find optimal lambda value that minimizes test MSE
best_lambda <- cv_model$ lambda . min
best_lambda

[1] 10.04567

#produce plot of test MSE by lambda value
plot(cv_model) 

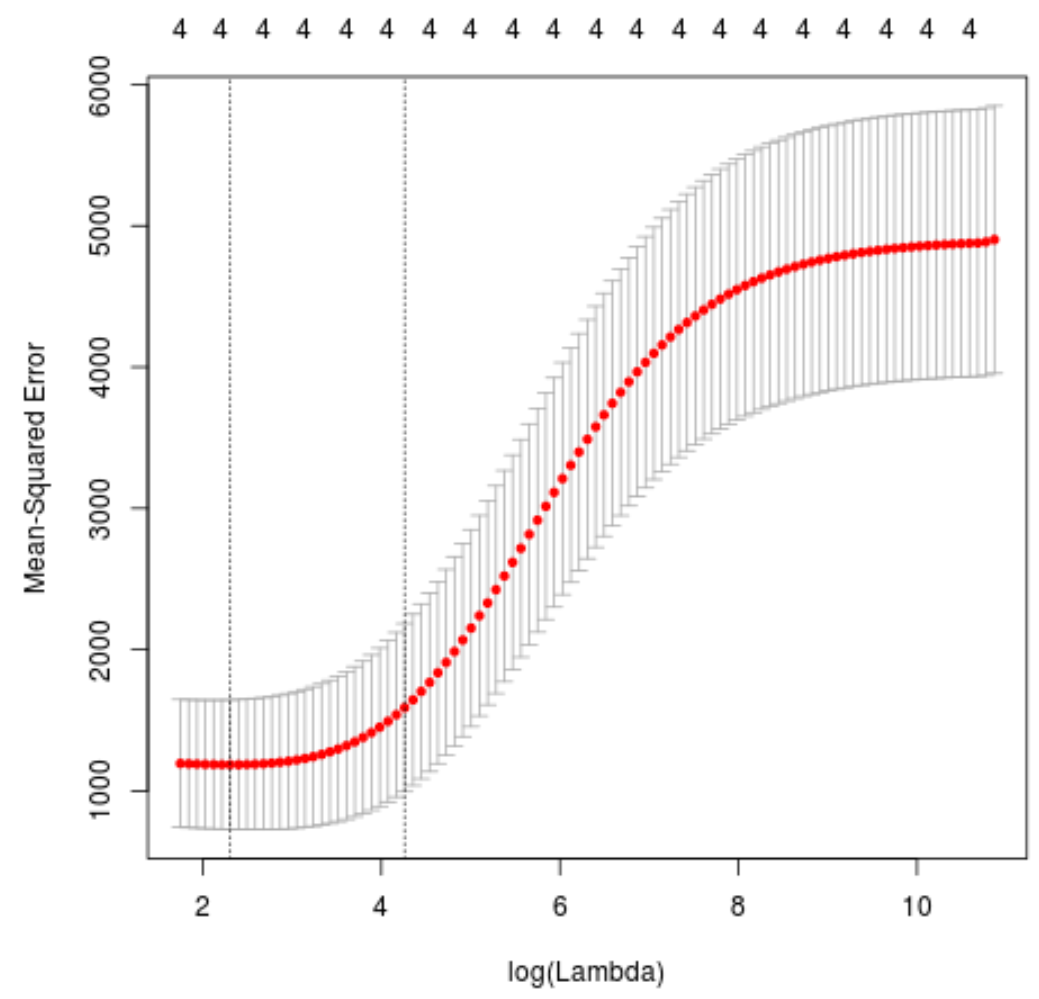
MSE testini minimuma indiren lambda değeri ise 10,04567 olarak çıkıyor.

4. Adım: Son modeli analiz edin

Son olarak optimal lambda değerinin ürettiği son modeli analiz edebiliriz.

Bu model için katsayı tahminlerini elde etmek için aşağıdaki kodu kullanabiliriz:

 #find coefficients of best model
best_model <- glmnet(x, y, alpha = 0 , lambda = best_lambda)
coef(best_model)

5 x 1 sparse Matrix of class "dgCMatrix"
                    s0
(Intercept) 475.242646
mpg -3.299732
wt 19.431238
drat -1.222429
qsec -17.949721

Ayrıca lambdadaki artışa bağlı olarak katsayı tahminlerinin nasıl değiştiğini görselleştirmek için bir İzleme grafiği de üretebiliriz:

 #produce Ridge trace plot
plot(model, xvar = " lambda ") 

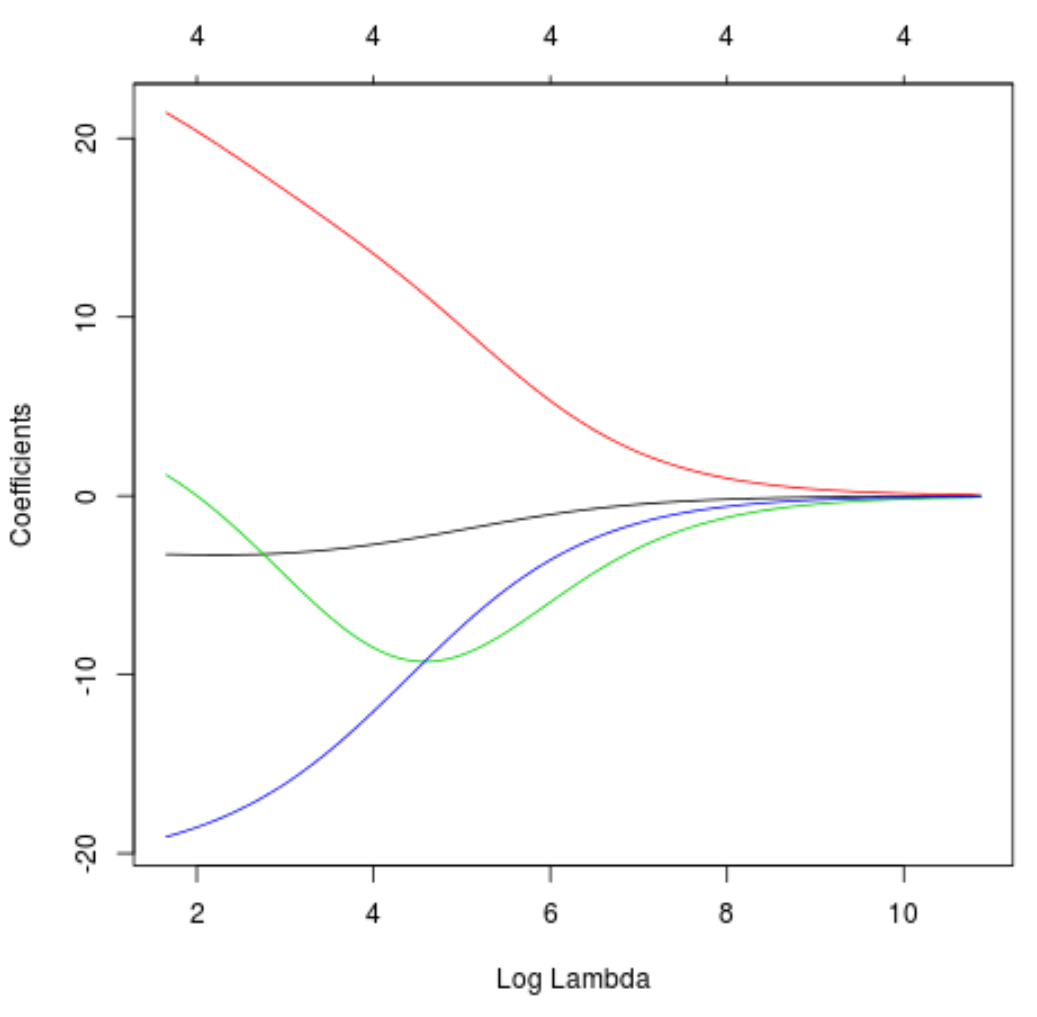
Son olarak modelin R-karesini eğitim verileri üzerinden hesaplayabiliriz:

 #use fitted best model to make predictions
y_predicted <- predict (model, s = best_lambda, newx = x)

#find OHS and SSE
sst <- sum ((y - mean (y))^2)
sse <- sum ((y_predicted - y)^2)

#find R-Squared
rsq <- 1 - sse/sst
rsq

[1] 0.7999513

R kare 0,7999513 olarak çıkıyor. Yani en iyi model, eğitim verilerinin yanıt değerlerindeki varyasyonun %79,99’unu açıklayabilmiştir.

Bu örnekte kullanılan R kodunun tamamını burada bulabilirsiniz.