R'de scheffe testi nasıl yapılır

Üç veya daha fazla bağımsız grubun ortalamaları arasında istatistiksel olarak anlamlı bir fark olup olmadığını belirlemek için tek yönlü ANOVA kullanılır.

ANOVA tablosunun genel p değeri belirli bir anlamlılık düzeyinin altındaysa, grup ortalamalarından en az birinin diğerlerinden farklı olduğunu söylemek için yeterli kanıtımız var demektir.

Ancak bu bize hangi grupların birbirinden farklı olduğunu söylemez. Bu bize basitçe tüm grup ortalamalarının eşit olmadığını söyler.

Hangi grupların birbirinden farklı olduğunu tam olarak bilmek için aile başına hata oranını kontrol edebilecek post-hoc bir test yapmamız gerekiyor.

En sık kullanılan post-hoc testlerden biri Scheffe testidir.

Bu eğitimde R’de Scheffe testinin nasıl gerçekleştirileceği açıklanmaktadır.

Örnek: R’de Scheffe testi

Bir öğretmenin üç farklı çalışma tekniğinin öğrenciler arasında farklı test puanlarına yol açıp açmadığını bilmek istediğini varsayalım. Bunu test etmek için rastgele 10 öğrenciyi her çalışma tekniğini kullanmaları için görevlendiriyor ve sınav sonuçlarını kaydediyor.

Üç grup arasındaki ortalama sınav puanları farklılıklarını test etmek amacıyla tek yönlü bir ANOVA uydurmak için R’de aşağıdaki adımları kullanabiliriz ve tam olarak hangi grupların farklı olduğunu belirlemek için Scheffe testini kullanabiliriz.

Adım 1: Veri kümesini oluşturun.

Aşağıdaki kod, 30 öğrencinin tamamının sınav sonuçlarını içeren bir veri kümesinin nasıl oluşturulacağını gösterir:

 #create data frame
data <- data.frame(technique = rep (c("tech1", "tech2", "tech3"), each = 10 ),
                   score = c(76, 77, 77, 81, 82, 82, 83, 84, 85, 89,
                             81, 82, 83, 83, 83, 84, 87, 90, 92, 93,
                             77, 78, 79, 88, 89, 90, 91, 95, 95, 98))

#view first six rows of data frame
head(data)

  technical score
1 tech1 76
2 tech1 77
3 tech1 77
4 tech1 81
5 tech1 82
6 tech1 82

Adım 2: Her grubun sınav sonuçlarını görüntüleyin.

Aşağıdaki kod, her grup için sınav sonuçlarının dağılımını görselleştirmek amacıyla kutu grafiklerinin nasıl oluşturulacağını gösterir:

 boxplot(score ~ technique,
        data = data,
        main = "Exam Scores by Studying Technique",
        xlab = "Studying Technique",
        ylab = "Exam Scores",
        col = "steelblue",
        border = "black")

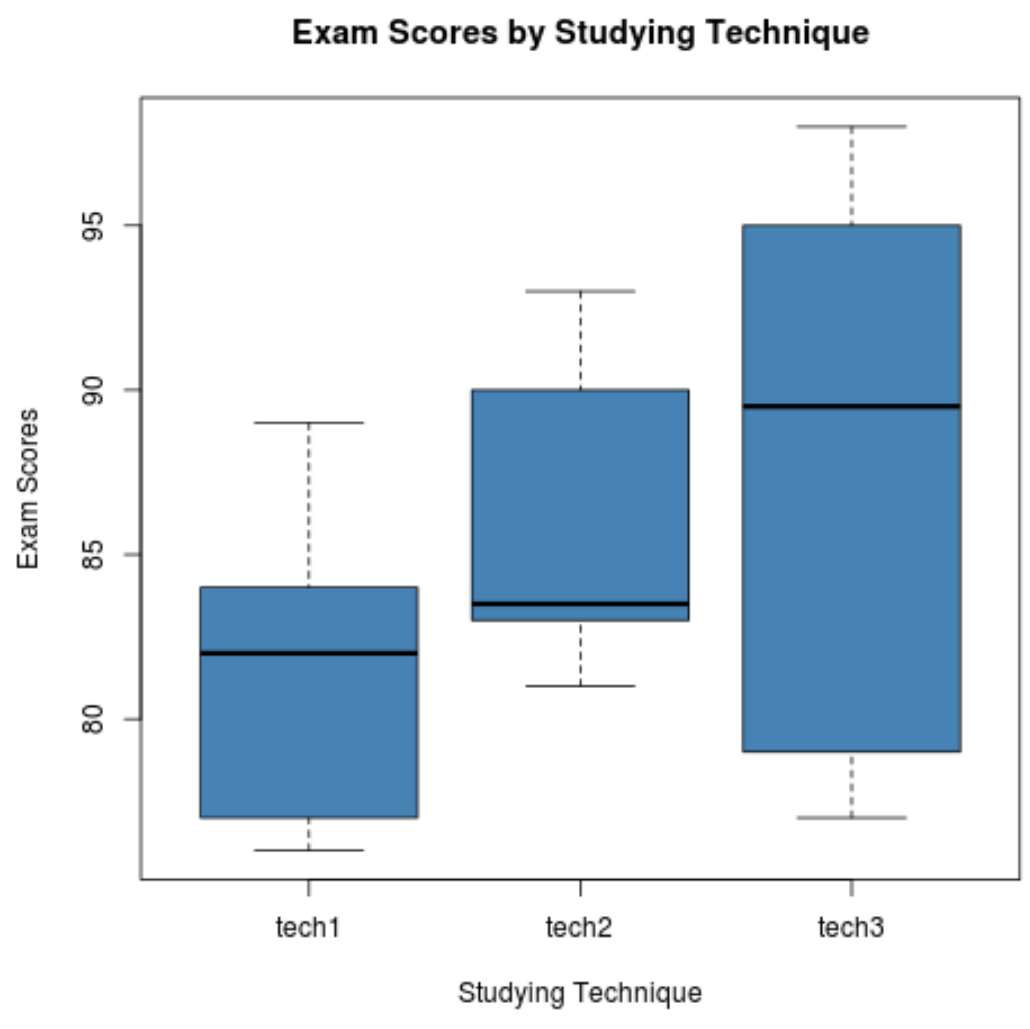
Adım 3: Tek yönlü ANOVA gerçekleştirin.

Aşağıdaki kod, her gruptaki ortalama sınav puanları arasındaki farkları test etmek için tek yönlü ANOVA’nın nasıl gerçekleştirileceğini gösterir:

 #fit the one-way ANOVA model
model <- aov(score ~ technique, data = data)

#view model output
summary(model)

            Df Sum Sq Mean Sq F value Pr(>F)  
technical 2 211.5 105.73 3.415 0.0476 *
Residuals 27 836.0 30.96                 
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Genel p değeri ( 0,0476 ) 0,05’ten küçük olduğundan bu durum her grubun aynı ortalama sınav puanına sahip olmadığını gösterir.

Daha sonra hangi grupların farklı olduğunu belirlemek için Scheffe testi yapacağız.

Adım 4: Scheffe testini gerçekleştirin.

Scheffe testini gerçekleştirmek için DescTools paketindeki ScheffeTest() fonksiyonunu kullanacağız.

Aşağıdaki kod, örneğimiz için bu işlevin nasıl kullanılacağını gösterir:

 #load DescTools package
library(DescTools)

#perform Scheffe's test
ScheffeTest(model)

  Posthoc multiple comparisons of means: Scheffe Test 
    95% family-wise confidence level

$technical
            diff lwr.ci upr.ci pval    
tech2-tech1 4.2 -2.24527202 10.645272 0.2582    
tech3-tech1 6.4 -0.04527202 12.845272 0.0519 .  
tech3-tech2 2.2 -4.24527202 8.645272 0.6803    

---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Sonucun yorumlanma şekli şu şekildedir:

• Teknik 2 ile teknik 1 arasındaki sınav sonuçlarındaki ortalama fark 4,2’dir . Ortalama farka karşılık gelen p değeri 0,2582’dir .
• Teknik 3 ile teknik 1 arasındaki sınav sonuçlarındaki ortalama fark 6,4’tür . Ortalama farka karşılık gelen p değeri 0,0519’dur .
• Teknik 3 ile teknik 2 arasındaki sınav sonuçlarındaki ortalama fark 2,2’dir . Ortalama farka karşılık gelen p değeri 0,6803’tür .

Hangi önem düzeyini kullanmaya karar verdiğimize bağlı olarak istatistiksel olarak anlamlı derecede farklı görünen yalnızca iki grup Teknik 3 ve Teknik 1’dir.

Ek kaynaklar

R’de tek yönlü ANOVA nasıl gerçekleştirilir
R’de Tukey testi nasıl yapılır?
R’de Bonferroni düzeltmesi nasıl yapılır