R'de uyum eksikliği testi nasıl yapılır (adım adım)

Tam regresyon modelinin, modelin azaltılmış versiyonuna göre veri setine önemli ölçüde daha iyi uyum sağlayıp sağlamadığını belirlemek için uyum eksikliği testi kullanılır.

Örneğin, belirli bir üniversitedeki öğrencilerin sınav puanlarını tahmin etmek için çalışılan saat sayısını kullanmak istediğimizi varsayalım. Aşağıdaki iki regresyon modelini uyarlamaya karar verebiliriz:

Tam model: puan = β ₀ + B ₁ (saat) + B ₂ (saat) ²

Azaltılmış model: puan = β ₀ + B ₁ (saat)

Aşağıdaki adım adım örnek, tam modelin azaltılmış modelden önemli ölçüde daha iyi bir uyum sağlayıp sağlamadığını belirlemek için R’de uyum eksikliği testinin nasıl gerçekleştirileceğini gösterir.

1. Adım: Veri kümesi oluşturun ve görselleştirin

İlk olarak, 50 öğrenci için çalışılan saat sayısını ve kazanılan sınav puanlarını içeren bir veri kümesi oluşturmak için aşağıdaki kodu kullanacağız:

 #make this example reproducible
set. seeds (1)

#create dataset
df <- data. frame (hours = runif (50, 5, 15), score=50)
df$score = df$score + df$hours^3/150 + df$hours* runif (50, 1, 2)

#view first six rows of data
head(df)

      hours score
1 7.655087 64.30191
2 8.721239 70.65430
3 10.728534 73.66114
4 14.082078 86.14630
5 7.016819 59.81595
6 13.983897 83.60510

Daha sonra saatlerle puan arasındaki ilişkiyi görselleştirmek için bir dağılım grafiği oluşturacağız:

 #load ggplot2 visualization package
library (ggplot2)

#create scatterplot
ggplot(df, aes (x=hours, y=score)) +
  geom_point() 

Adım 2: İki farklı modeli veri kümesine yerleştirin

Daha sonra veri kümesine iki farklı regresyon modeli yerleştireceğiz:

 #fit full model
full <- lm(score ~ poly (hours,2), data=df)

#fit reduced model
reduced <- lm(score ~ hours, data=df)

3. Adım: Uyum eksikliği testi yapın

Daha sonra, iki model arasında uyum eksikliği testi gerçekleştirmek için anova() komutunu kullanacağız:

 #lack of fit test
anova(full, reduced)

Analysis of Variance Table

Model 1: score ~ poly(hours, 2)
Model 2: score ~ hours
  Res.Df RSS Df Sum of Sq F Pr(>F)   
1 47 368.48                                
2 48 451.22 -1 -82.744 10.554 0.002144 **
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

F testi istatistiği 10,554 ve buna karşılık gelen p değeri 0,002144 olarak ortaya çıkıyor. Bu p değeri 0,05’ten küçük olduğundan testin sıfır hipotezini reddedebilir ve tam modelin indirgenmiş modele göre istatistiksel olarak anlamlı derecede daha iyi bir uyum sağladığı sonucuna varabiliriz.

4. Adım: Son modeli görselleştirin

Son olarak, nihai modeli (tam model) orijinal veri kümesine göre görselleştirebiliriz:

 ggplot(df, aes (x=hours, y=score)) + 
          geom_point() +
          stat_smooth(method=' lm ', formula = y ~ poly (x,2), size = 1) + 
          xlab(' Hours Studied ') +
          ylab(' Score ') 

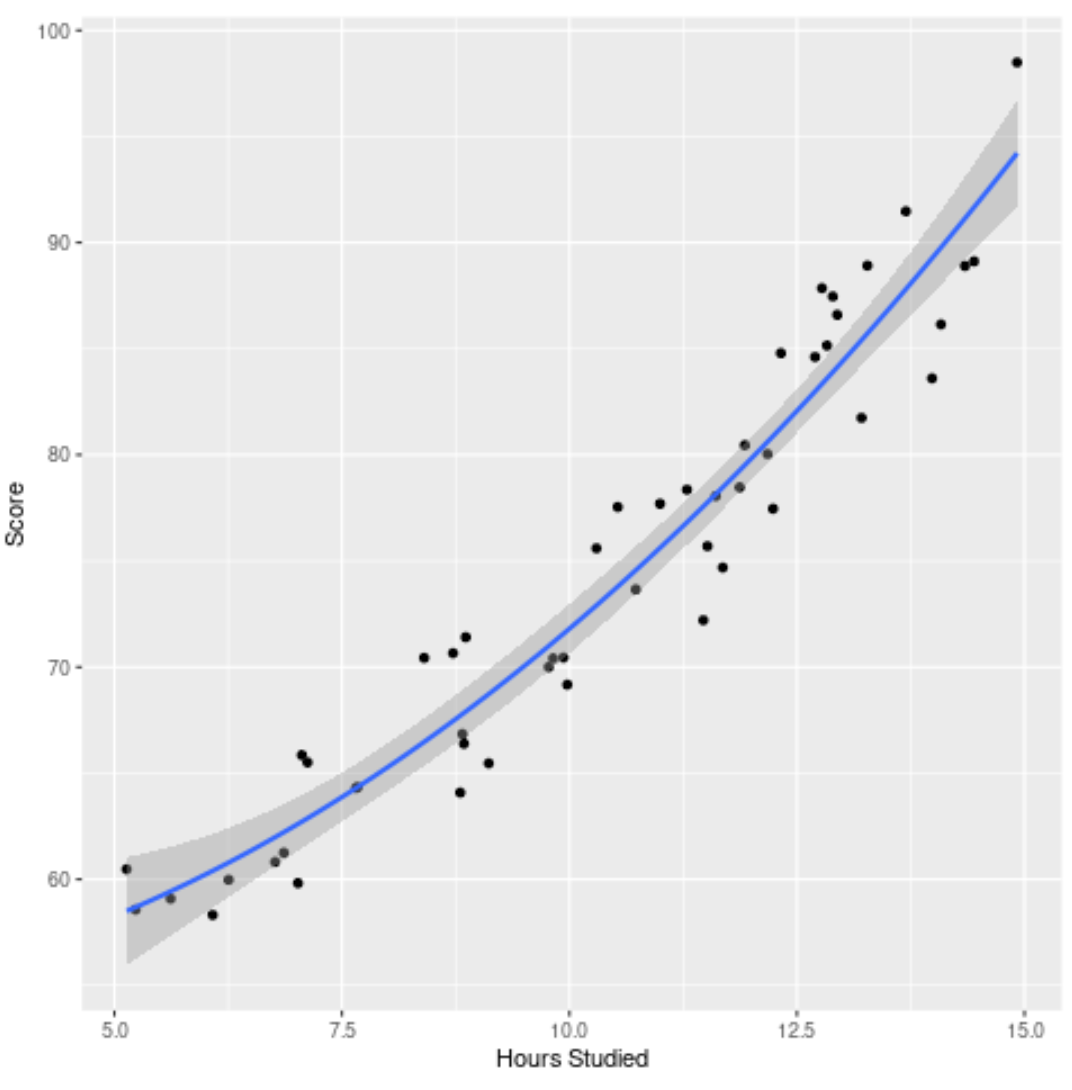
Model eğrisinin verilere oldukça iyi uyum sağladığını görebiliriz.

Ek kaynaklar

R’de basit doğrusal regresyon nasıl gerçekleştirilir
R’de çoklu doğrusal regresyon nasıl gerçekleştirilir
R’de polinom regresyonu nasıl gerçekleştirilir