Welch'in t testi r'de nasıl gerçekleştirilir?

Welch t testi, iki grubun eşit varyansa sahip olduğu varsayılmadığında , iki bağımsız grup arasındaki ortalamaları karşılaştırmak için kullanılır.

Welch’in t testini R’de gerçekleştirmek için aşağıdaki sözdizimini kullanan t.test() işlevini kullanabiliriz:

t.test(x, y, alternatif = c(“iki yüz”, “daha az”, “daha büyük”))

Altın:

• x: birinci grup için veri değerlerinin sayısal bir vektörü
• y: ikinci grup için veri değerlerinin sayısal bir vektörü
• alternatif: test için alternatif hipotez. Varsayılan çift taraflıdır.

Aşağıdaki örnek, R’de Welch t testini gerçekleştirmek için bu işlevin nasıl kullanılacağını gösterir.

Örnek: Welch’in R’deki t testi

Bir öğretmen, sınava hazırlanmak için sınava hazırlık kitapçığı kullanan 12 öğrencinin sınav sonuçlarını kullanmayan 12 öğrenciyle karşılaştırmak istiyor.

Aşağıdaki vektörler her gruptaki öğrencilerin sınav sonuçlarını göstermektedir:

 booklet <- c(90, 85, 88, 89, 94, 91, 79, 83, 87, 88, 91, 90)
no_booklet <- c(67, 90, 71, 95, 88, 83, 72, 66, 75, 86, 93, 84)

Welch t-testini gerçekleştirmeden önce, her grup için puanların dağılımını görselleştirmek üzere ilk olarak kutu grafikleri oluşturabiliriz:

 boxplot(booklet, no_booklet, names =c(" Booklet "," No Booklet "))

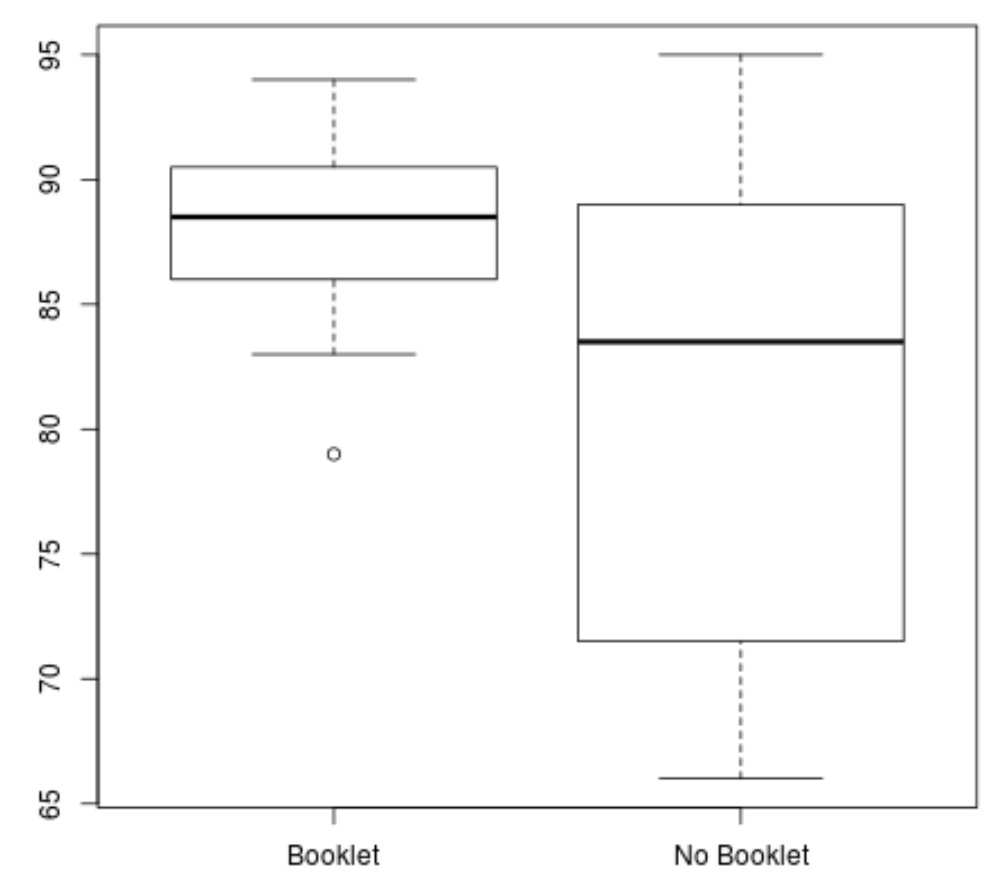
“Kitapçık” grubunun ortalama puanının daha yüksek, puan farkının ise daha düşük olduğunu açıkça görebiliyoruz.

Gruplar arasındaki ortalama puanların önemli ölçüde farklı olup olmadığını resmi olarak test etmek için Welch t-testini uygulayabiliriz:

 #perform Welch's t-test
t.test(booklet, no_booklet)

	Welch Two Sample t-test

data: booklet and no_booklet
t = 2.2361, df = 14.354, p-value = 0.04171
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
  0.3048395 13.8618272
sample estimates:
mean of x mean of y 
 87.91667 80.83333 

Sonuçtan t testi istatistiğinin 2,2361 ve karşılık gelen p değerinin 0,04171 olduğunu görebiliriz.

Bu p değeri 0,05’ten küçük olduğundan sıfır hipotezini reddedebilir ve iki grup arasında ortalama sınav puanları arasında istatistiksel olarak anlamlı bir fark olduğu sonucuna varabiliriz.

t.test() işlevi ayrıca bize aşağıdaki bilgileri de sağlar:

• İki grup arasındaki ortalama sınav puanları farkına ilişkin %95 güven aralığı [0,3048, 13,8618 ]’dir.
• Birinci grubun ortalama sınav puanı 87,91667’dir .
• İkinci grubun ortalama sınav puanı 80.83333’tür .

t.test() işlevine ilişkin tüm belgeleri burada bulabilirsiniz.

Ek kaynaklar

Aşağıdaki eğitimlerde R’de diğer ortak görevlerin nasıl gerçekleştirileceği açıklanmaktadır:

R’de tek örnekli t testi nasıl yapılır
R’de iki örnekli t testi nasıl yapılır
R’de eşleştirilmiş örnekler t testi nasıl yapılır
R’de tek bir grafikte birden fazla kutu grafiği nasıl çizilir