R'de dağılım grafiği matrisi nasıl oluşturulur (2 örnek)

Dağılım grafiği matrisi , bir veri kümesindeki farklı değişkenler arasındaki ikili ilişkiyi anlamanıza olanak tanıyan bir dağılım grafiği matrisidir.

R’de dağılım grafiği matrisi oluşturmanın iki yaygın yolu vardır:

Yöntem 1: Base R’yi kullanın

 #create scatterplot matrix (pch=20 means to use a solid circle for points)
plot(df, pch= 20 )

Yöntem 2: ggplot2 ve GGally paketlerini kullanın

 library (ggplot2)
library (GGally)

#create scatterplot matrix
ggpairs(df)

Aşağıdaki örnekler, R’deki aşağıdaki veri çerçevesiyle her yöntemin pratikte nasıl kullanılacağını gösterir:

 #create data frame
df <- data. frame (points=c(99, 90, 86, 88, 95, 99, 101, 104),
                 assists=c(33, 28, 31, 39, 40, 40, 35, 47),
                 rebounds=c(30, 28, 24, 24, 20, 20, 15, 12))

#view first few rows of data frame
head(df)

  points assists rebounds
1 99 33 30
2 90 28 28
3 86 31 24
4 88 39 24
5 95 40 20
6 99 40 20

Örnek 1: R Tabanını Kullanarak Dağılım Grafiği Matrisi Oluşturma

Veri çerçevemizdeki her değişken için bir dağılım grafiği matrisi oluşturmak amacıyla temel R grafiği() işlevini kullanabiliriz:

 #create scatterplot matrix
plot(df, pch= 20 , cex= 1.5 , col=' steelblue ')

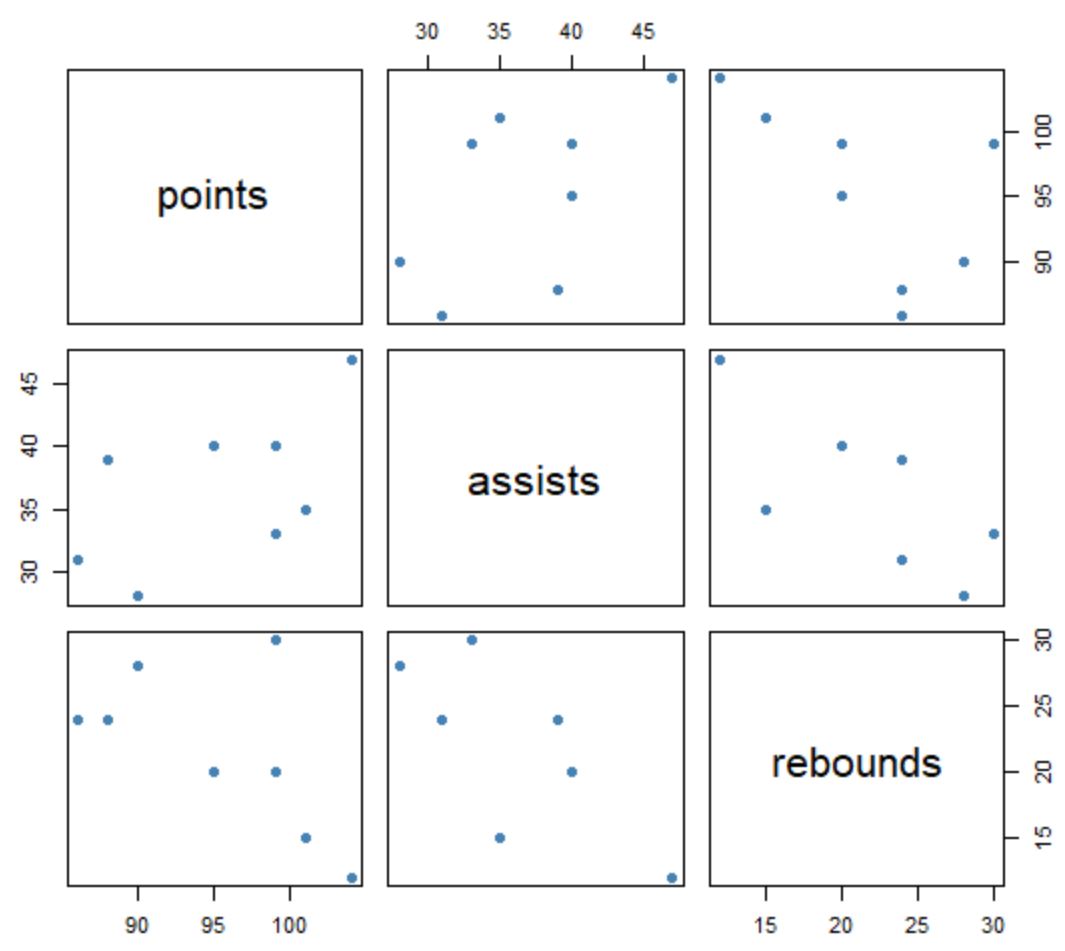
Matrisin yorumlanma şekli şu şekildedir:

• Değişken adları çapraz kutular boyunca görüntülenir.
• Diğer tüm kutular, değişkenlerin ikili kombinasyonlarının her biri arasındaki ilişkinin dağılım grafiğini görüntüler. Örneğin, matrisin sağ üst köşesindeki kutu, sayı ve ribaund değerlerinin dağılım grafiğini görüntüler. Sol orta alan, puanlar ve asistler vb. için değerlerin dağılım grafiğini gösterir.

Cex’in yoldaki noktaların boyutunu, col’un ise noktaların rengini kontrol ettiğini unutmayın.

Örnek 2: ggplot2 ve GGally Kullanarak Bir Dağılım Grafiği Matrisi Oluşturma

Veri çerçevemizdeki her değişken için bir dağılım grafiği matrisi oluşturmak amacıyla R’deki ggplot2 ve GGally paketlerindeki ggpairs() işlevini de kullanabiliriz:

 library (ggplot2)
library (GGally)

#create scatterplot matrix
ggpairs(df) 

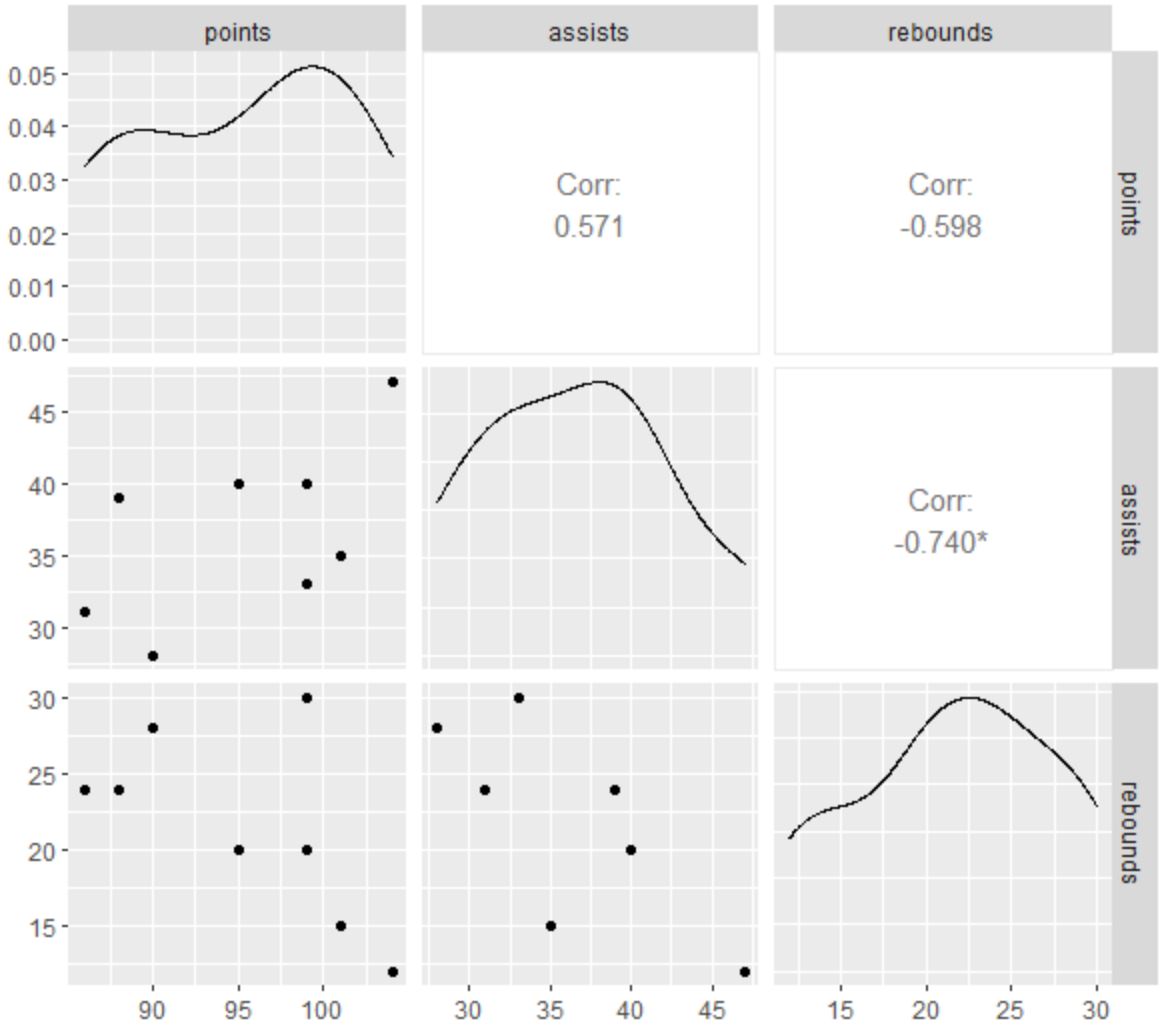
Bu dağılım grafiği matrisi, R baseplot() işleviyle aynı dağılım grafiklerini içerir, ancak buna ek olarak her bir değişken için bir yoğunluk grafiğinin yanı sıra değişkenlerin her ikili kombinasyonu arasındaki korelasyon katsayısını da görebiliriz.

Örneğin şunu görebiliriz:

• Asistlerle sayılar arasındaki korelasyon katsayısı 0,571’dir .
• Ribaundlarla sayılar arasındaki korelasyon katsayısı -0,598’dir .
• Ribaund ve asist arasındaki korelasyon katsayısı -0,740’tır .

-0,740’ın yanındaki küçük yıldız ( * ) da ribauntlarla asistler arasındaki ilişkinin istatistiksel olarak anlamlı olduğunu gösteriyor.

Ek kaynaklar

Aşağıdaki eğitimlerde R’de diğer ortak görevlerin nasıl gerçekleştirileceği açıklanmaktadır:

R’de korelasyon matrisi nasıl oluşturulur
R’de gruba göre nokta bulutları nasıl oluşturulur