R'de dfbetas nasıl hesaplanır

İstatistikte genellikle farklı gözlemlerin regresyon modellerinde ne gibi etkileri olduğunu bilmek isteriz.

Gözlemlerin etkisini hesaplamanın bir yolu, DFBETAS olarak bilinen ve bize her bir gözlemin kaldırılmasının her katsayısı üzerindeki standartlaştırılmış etkiyi söyleyen bir ölçüm kullanmaktır.

Bu ölçüm bize, belirli bir regresyon modelinde her gözlemin her katsayı tahmini üzerindeki etkisi hakkında bir fikir verir.

Bu eğitimde, R’deki bir modeldeki her gözlem için DFBETAS’ın nasıl hesaplanacağı ve görselleştirileceğine ilişkin adım adım bir örnek gösterilmektedir.

1. Adım: Bir regresyon modeli oluşturun

İlk olarak, R’de yerleşik mtcars veri kümesini kullanarak çoklu doğrusal regresyon modeli oluşturacağız:

 #fit a regression model
model <- lm(mpg~disp+hp, data=mtcars)

#view model summary
summary(model)

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) 30.735904 1.331566 23.083 < 2nd-16 ***
available -0.030346 0.007405 -4.098 0.000306 ***
hp -0.024840 0.013385 -1.856 0.073679 .  
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.127 on 29 degrees of freedom
Multiple R-squared: 0.7482, Adjusted R-squared: 0.7309 
F-statistic: 43.09 on 2 and 29 DF, p-value: 2.062e-09

Adım 2: Her gözlem için DFBETAS’ı hesaplayın

Daha sonra, modeldeki her gözlem için DFBETAS değerlerini hesaplamak amacıyla yerleşik dfbetas() fonksiyonunu kullanacağız:

 #calculate DFBETAS for each observation in the model
dfbetas <- as . data . frame (dfbetas(model))

#display DFBETAS for each observation
dfbetas

                      (Intercept) disp hp
Mazda RX4 -0.1174171253 0.030760632 1.748143e-02
Mazda RX4 Wag -0.1174171253 0.030760632 1.748143e-02
Datsun 710 -0.1694989349 0.086630144 -3.332781e-05
Hornet 4 Drive 0.0577309674 0.078971334 -8.705488e-02
Hornet Sportabout -0.0204333878 0.237526523 -1.366155e-01
Valiant -0.1711908285 -0.139135639 1.829038e-01
Duster 360 -0.0312338677 -0.005356209 3.581378e-02
Merc 240D -0.0312259577 -0.010409922 2.433256e-02
Merc 230 -0.0865872595 0.016428917 2.287867e-02
Merc 280 -0.1560683502 0.078667906 -1.911180e-02
Merc 280C -0.2254489597 0.113639937 -2.760800e-02
Merc 450SE 0.0022844093 0.002966155 -2.855985e-02
Merc 450SL 0.0009062022 0.001176644 -1.132941e-02
Merc 450SLC 0.0041566755 0.005397169 -5.196706e-02
Cadillac Fleetwood 0.0388832216 -0.134511133 7.277283e-02
Lincoln Continental 0.0483781688 -0.121146607 5.326220e-02
Chrysler Imperial -0.1645266331 0.236634429 -3.917771e-02
Fiat 128 0.5720358325 -0.181104179 -1.265475e-01
Honda Civic 0.3490872162 -0.053660545 -1.326422e-01
Toyota Corolla 0.7367058819 -0.268512348 -1.342384e-01
Toyota Corona -0.2181110386 0.101336902 5.945352e-03
Dodge Challenger -0.0270169005 -0.123610713 9.441241e-02
AMC Javelin -0.0406785103 -0.141711468 1.074514e-01
Camaro Z28 0.0390139262 0.012846225 -5.031588e-02
Pontiac Firebird -0.0549059340 0.574544346 -3.689584e-01
Fiat X1-9 0.0565157245 -0.017751582 -1.262221e-02
Porsche 914-2 0.0839169111 -0.028670987 -1.240452e-02
Lotus Europa 0.3444562478 -0.402678927 2.135224e-01
Ford Pantera L -0.1598854695 -0.094184733 2.320845e-01
Ferrari Dino -0.0343997122 0.248642444 -2.344154e-01
Maserati Bora -0.3436265545 -0.511285637 7.319066e-01
Volvo 142E -0.1784974091 0.132692956 -4.433915e-02

Her gözlem için, söz konusu gözlemi kaldırdığımızda ortaya çıkan orijin, disp değişkeni ve hp değişkeni için katsayı tahminindeki farkı görebiliriz.

Genel olarak, bir gözlemin, n’nin gözlem sayısı olduğu 2/√ n eşiğinden daha büyük bir DBETAS değerine sahip olması durumunda, belirli bir katsayının tahmini üzerinde güçlü bir etkiye sahip olduğunu düşünüyoruz.

Bu örnekte eşik 0,3535534 olacaktır:

 #find number of observations
n <- nrow (mtcars)

#calculate DFBETAS threshold value
thresh <- 2/ sqrt (n)

thresh

[1] 0.3535534

Adım 3: DFBETAS’ı görselleştirin

Son olarak, modeldeki her gözlem ve her tahminci için DFBETAS değerini görselleştirmek üzere grafikler oluşturabiliriz:

 #specify 2 rows and 1 column in plotting region
by(mfrow=c(2,1))

#plot DFBETAS for disp with threshold lines
plot(dfbetas$disp, type=' h ')
abline(h = thresh, lty = 2)
abline(h = -thresh, lty = 2)

#plot DFBETAS for hp with threshold lines 
plot(dfbetas$hp, type=' h ')
abline(h = thresh, lty = 2)
abline(h = -thresh, lty = 2)

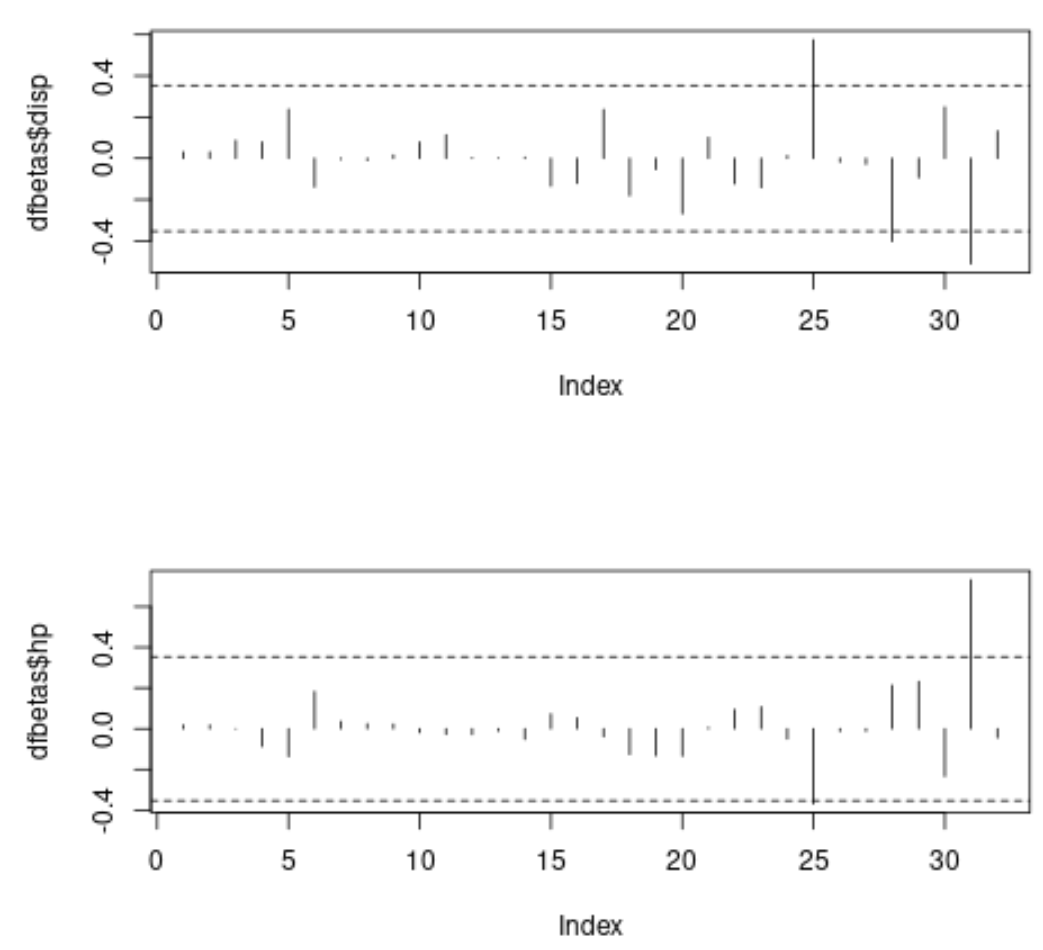
Her çizimde, x ekseni veri kümesindeki her gözlemin indeksini görüntüler ve y değeri, her gözlem ve her tahminci için karşılık gelen DFBETAS’ı görüntüler.

İlk grafikte üç gözlemin 0,3535534 mutlak eşik değerini aştığını görebiliriz ve ikinci grafikte iki gözlemin mutlak eşik değerini aştığını görebiliriz.

Model katsayılarının tahmini üzerinde aşırı bir etkiye sahip olup olmadıklarını belirlemek için bu gözlemleri daha yakından incelemeyi seçebiliriz.

Ek kaynaklar

R’de basit doğrusal regresyon nasıl gerçekleştirilir
R’de çoklu doğrusal regresyon nasıl gerçekleştirilir
R’de kaldıraç istatistikleri nasıl hesaplanır
R’de DFFITS nasıl hesaplanır