R'deki k-medoids: adım adım örnek

Kümeleme, bir veri seti içindeki gözlem gruplarını veya kümelerini bulmaya çalışan bir makine öğrenme tekniğidir.

Amaç, her küme içindeki gözlemlerin birbirine oldukça benzer olduğu, farklı kümelerdeki gözlemlerin ise birbirinden oldukça farklı olduğu kümeleri bulmaktır.

Kümeleme bir denetimsiz öğrenme biçimidir çünkü biz bir yanıt değişkeninin değerini tahmin etmek yerine yalnızca bir veri kümesi içindeki yapıyı bulmaya çalışıyoruz.

Kümeleme genellikle işletmelerin aşağıdaki gibi bilgilere erişimi olduğunda pazarlamada kullanılır:

• Hane geliri
• Ev büyüklüğü
• Hane Reisi Mesleği
• En yakın kentsel alana uzaklık

Bu bilgi mevcut olduğunda kümeleme, benzer olan ve belirli ürünleri satın alma veya belirli bir reklam türüne daha iyi yanıt verme olasılığı daha yüksek olan haneleri belirlemek için kullanılabilir.

Kümelemenin en yaygın biçimlerinden biri k-ortalama kümelemesi olarak bilinir.

Ne yazık ki, bu yöntem aykırı değerlerden etkilenebilir; bu nedenle sıklıkla kullanılan bir alternatif k-medoids kümelemesidir .

K-Medoids kümelemesi nedir?

K-medoids kümelemesi, bir veri kümesindeki her gözlemi K kümelerinden birine yerleştirdiğimiz bir tekniktir.

Nihai amaç, her küme içindeki gözlemlerin birbirine oldukça benzer olduğu, farklı kümelerdeki gözlemlerin ise birbirinden oldukça farklı olduğu K kümeye sahip olmaktır.

Uygulamada, K-aracı kümelemesini gerçekleştirmek için aşağıdaki adımları kullanırız:

1. K için bir değer seçin.

• Öncelikle veride kaç tane küme tanımlamak istediğimize karar vermemiz gerekiyor. Çoğunlukla K için birkaç farklı değeri test etmemiz ve belirli bir problem için hangi sayıda kümenin en anlamlı göründüğünü görmek için sonuçları analiz etmemiz gerekir.

2. Her gözlemi rastgele olarak 1’den K’ye kadar bir başlangıç kümesine atayın.

3. Küme atamalarının değişmesi durana kadar aşağıdaki prosedürü uygulayın.

• Her K kümesi için kümenin ağırlık merkezini hesaplayın. Bu, k’inci kümenin gözlemlerine ilişkin özelliklerin p medyanlarının vektörüdür.
• Her gözlemi en yakın merkeze sahip kümeye atayın. Burada en yakın , Öklid mesafesi kullanılarak tanımlanır.

Teknik not:

K-medoids, küme ağırlık merkezlerini ortalamalar yerine medyanlar kullanarak hesapladığından, aykırı değerlere karşı k-ortalamalara göre daha dayanıklı olma eğilimindedir.

Uygulamada, eğer veri setinde aşırı aykırı değerler yoksa, k-ortalamalar ve k-medoidler benzer sonuçlar üretecektir.

R’de kümelenen K-Medoidler

Aşağıdaki eğitimde, R’de k-medoids kümelemesinin nasıl gerçekleştirileceğine ilişkin adım adım bir örnek sağlanmaktadır.

Adım 1: Gerekli paketleri yükleyin

İlk olarak, R’de k-medoids kümelemesi için çeşitli yararlı işlevler içeren iki paket yükleyeceğiz.

 library (factoextra)
library (cluster)

2. Adım: Verileri Yükleyin ve Hazırlayın

Bu örnek için, 1973’te her ABD eyaletinde 100.000 kişi başına cinayet , saldırı ve tecavüz nedeniyle tutuklananların sayısını ve ayrıca her eyaletin kentsel bölgelerde yaşayan nüfusunun yüzdesini içeren R’de yerleşik USArrests veri kümesini kullanacağız. alanlar. , UrbanPop .

Aşağıdaki kod aşağıdakilerin nasıl yapılacağını gösterir:

• USArrests veri kümesini yükle
• Eksik değerleri olan tüm satırları kaldırın
• Veri kümesindeki her değişkeni ortalama 0 ve standart sapma 1 olacak şekilde ölçeklendirin

 #load data
df <-USArrests

#remove rows with missing values
df <- na. omitted (df)

#scale each variable to have a mean of 0 and sd of 1
df <- scale(df)

#view first six rows of dataset
head(df)

               Murder Assault UrbanPop Rape
Alabama 1.24256408 0.7828393 -0.5209066 -0.003416473
Alaska 0.50786248 1.1068225 -1.2117642 2.484202941
Arizona 0.07163341 1.4788032 0.9989801 1.042878388
Arkansas 0.23234938 0.2308680 -1.0735927 -0.184916602
California 0.27826823 1.2628144 1.7589234 2.067820292
Colorado 0.02571456 0.3988593 0.8608085 1.864967207

Adım 3: En uygun küme sayısını bulun

R’de k-medoid kümelemeyi gerçekleştirmek için, “ortancaların etrafında bölümleme” anlamına gelen ve aşağıdaki sözdizimini kullanan pam() işlevini kullanabiliriz:

pam(veri, k, metrik = “Öklidyen”, stand = YANLIŞ)

Altın:

• veri: Veri kümesinin adı.
• k: Küme sayısı.
• Metrik: Mesafeyi hesaplamak için kullanılacak metrik. Varsayılan Öklid’dir ancak manhattan’ı da belirtebilirsiniz.
• stand: Veri kümesindeki her değişkenin normalize edilip edilmeyeceği. Varsayılan değer false’tur.

Hangi küme sayısının optimal olduğunu önceden bilmediğimizden, karar vermemize yardımcı olabilecek iki farklı grafik oluşturacağız:

1. Kareler toplamına göre küme sayısı

İlk olarak, küme sayısı ile kareler toplamı toplamının grafiğini oluşturmak için fviz_nbclust() işlevini kullanacağız:

 fviz_nbclust(df, pam, method = “ wss ”) 

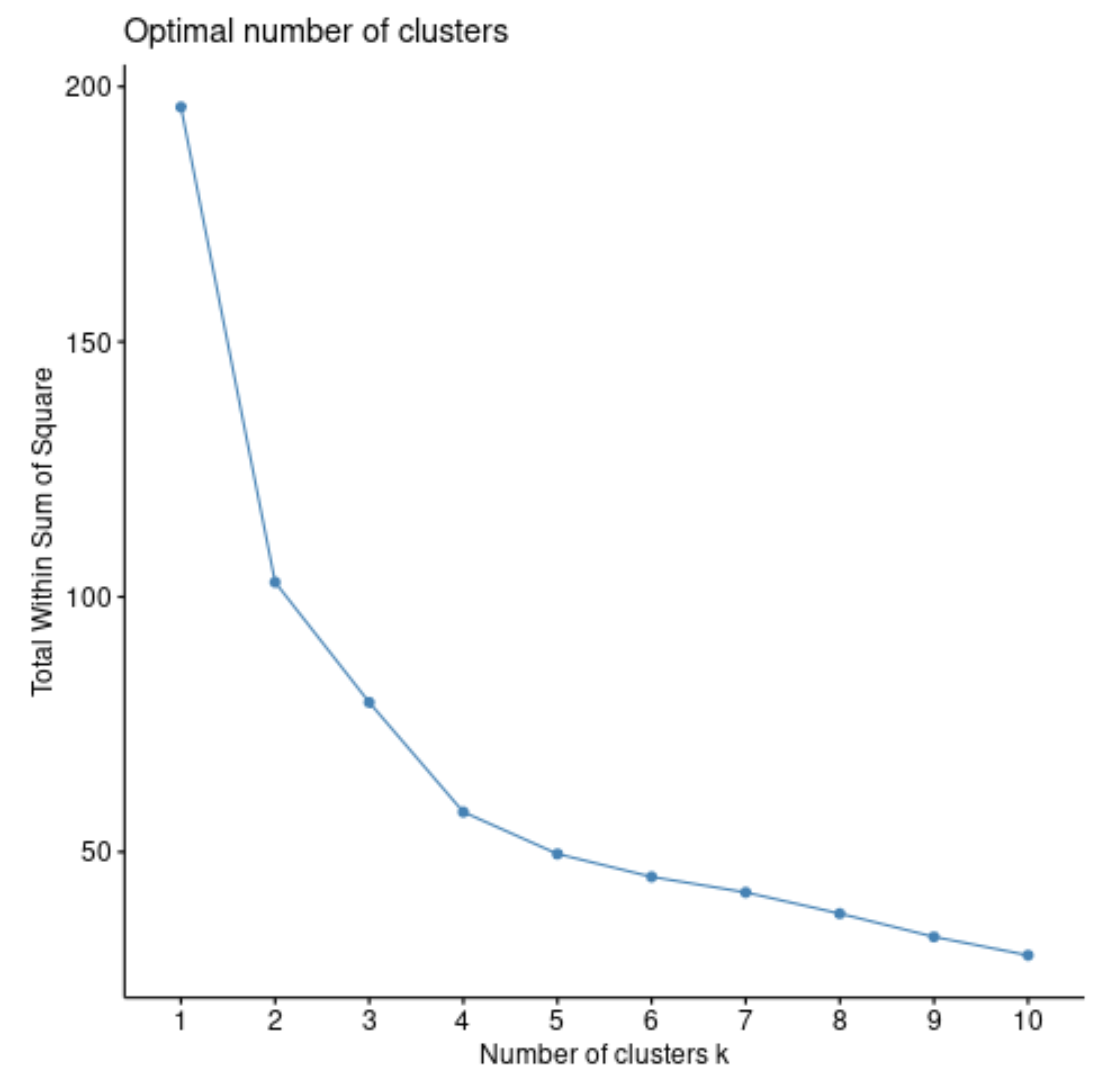
Küme sayısını artırdıkça kareler toplamındaki toplam genellikle her zaman artacaktır. Dolayısıyla, bu tür bir olay örgüsü oluşturduğumuzda, karelerin toplamının “bükülmeye” veya düzleşmeye başladığı bir “diz” arıyoruz.

Grafiğin eğrilik noktası genellikle optimal küme sayısına karşılık gelir. Bu rakamın ötesinde aşırı uyumun meydana gelmesi muhtemeldir.

Bu grafik için k = 4 kümede küçük bir bükülme veya “bükülme” olduğu görülmektedir.

2. Küme sayısı ve boşluk istatistikleri

Optimum küme sayısını belirlemenin bir başka yolu , sapma istatistiği adı verilen ve farklı k değerleri için toplam küme içi varyasyonu, kümelenme olmayan bir dağılım için beklenen değerleriyle karşılaştıran bir ölçüm kullanmaktır.

Küme paketindeki clusGap() işlevini kullanarak her küme sayısı için boşluk istatistiğini ve ayrıca fviz_gap_stat() işlevini kullanarak kümelerin boşluk istatistiklerine karşı grafiğini hesaplayabiliriz:

 #calculate gap statistic based on number of clusters
gap_stat <- clusGap(df,
                    FUN = pam,
                    K.max = 10, #max clusters to consider
                    B = 50) #total bootstrapped iterations

#plot number of clusters vs. gap statistic
fviz_gap_stat(gap_stat) 

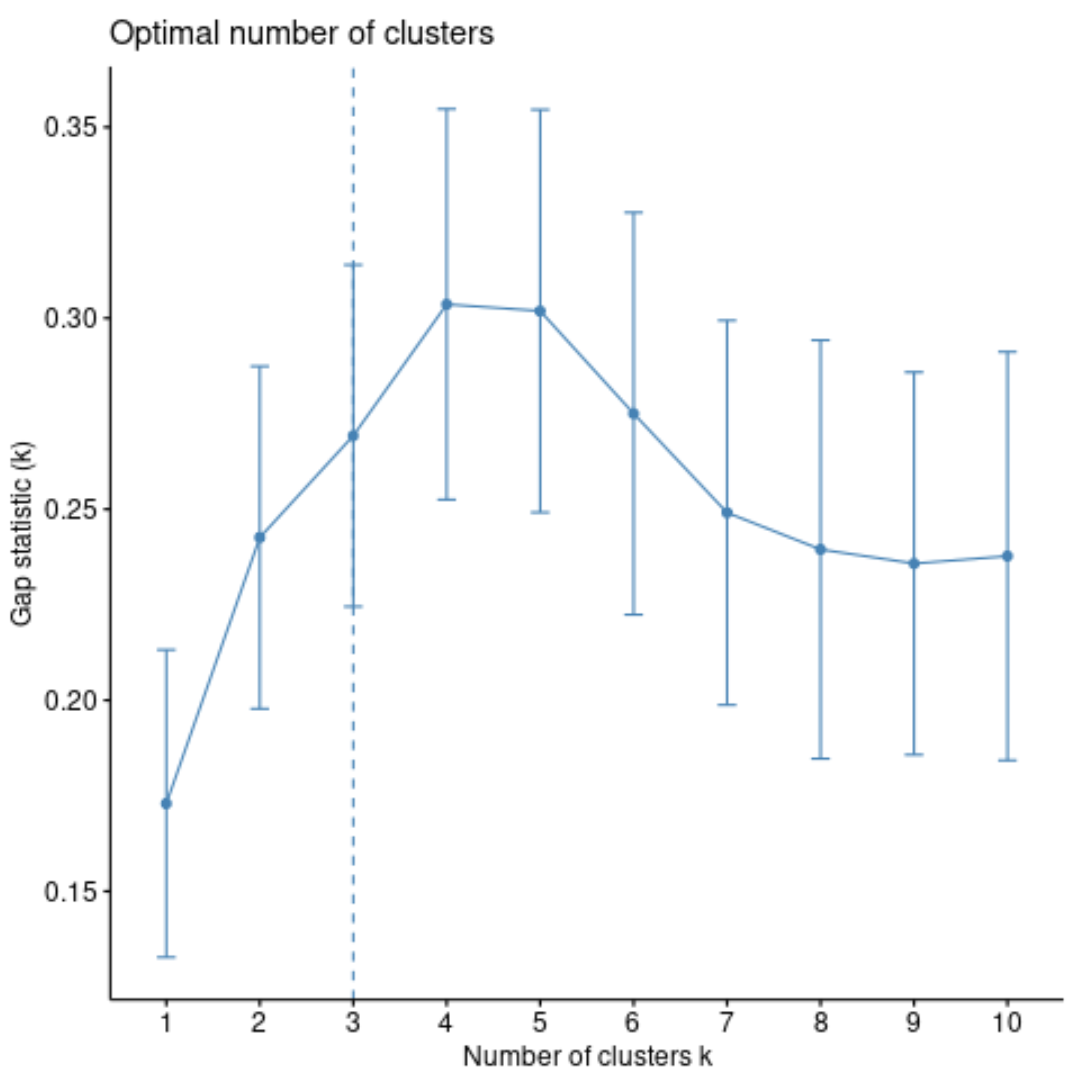
Grafikten boşluk istatistiğinin k = 4 kümede en yüksek olduğunu görebiliriz, bu da daha önce kullandığımız dirsek yöntemine karşılık gelir.

Adım 4: Optimal K ile K-Medoids kümelemesini gerçekleştirin

Son olarak, k 4’ün optimal değerini kullanarak veri kümesi üzerinde k-medoids kümelemesini gerçekleştirebiliriz:

 #make this example reproducible
set.seed(1)

#perform k-medoids clustering with k = 4 clusters
kmed <- pam(df, k = 4)

#view results
kmed

              ID Murder Assault UrbanPop Rape
Alabama 1 1.2425641 0.7828393 -0.5209066 -0.003416473
Michigan 22 0.9900104 1.0108275 0.5844655 1.480613993
Oklahoma 36 -0.2727580 -0.2371077 0.1699510 -0.131534211
New Hampshire 29 -1.3059321 -1.3650491 -0.6590781 -1.252564419
Vector clustering:
       Alabama Alaska Arizona Arkansas California 
             1 2 2 1 2 
      Colorado Connecticut Delaware Florida Georgia 
             2 3 3 2 1 
        Hawaii Idaho Illinois Indiana Iowa 
             3 4 2 3 4 
        Kansas Kentucky Louisiana Maine Maryland 
             3 3 1 4 2 
 Massachusetts Michigan Minnesota Mississippi Missouri 
             3 2 4 1 3 
       Montana Nebraska Nevada New Hampshire New Jersey 
             3 3 2 4 3 
    New Mexico New York North Carolina North Dakota Ohio 
             2 2 1 4 3 
      Oklahoma Oregon Pennsylvania Rhode Island South Carolina 
             3 3 3 3 1 
  South Dakota Tennessee Texas Utah Vermont 
             4 1 2 3 4 
      Virginia Washington West Virginia Wisconsin Wyoming 
             3 3 4 4 3 
Objective function:
   build swap 
1.035116 1.027102 

Available components:
 [1] "medoids" "id.med" "clustering" "objective" "isolation" 
 [6] "clusinfo" "silinfo" "diss" "call" "data"          

Dört küme merkezinin tamamının veri kümesindeki gerçek gözlemler olduğunu unutmayın. Çıktının üst kısmına yakın bir yerde, dört merkezin aşağıdaki durumlar olduğunu görebiliriz:

• Alabama
• Michigan
• Oklahoma
• New Hampshire

fivz_cluster() işlevini kullanarak eksenlerdeki ilk iki ana bileşeni görüntüleyen bir dağılım grafiğinde kümeleri görselleştirebiliriz:

 #plot results of final k-medoids model
fviz_cluster(kmed, data = df)

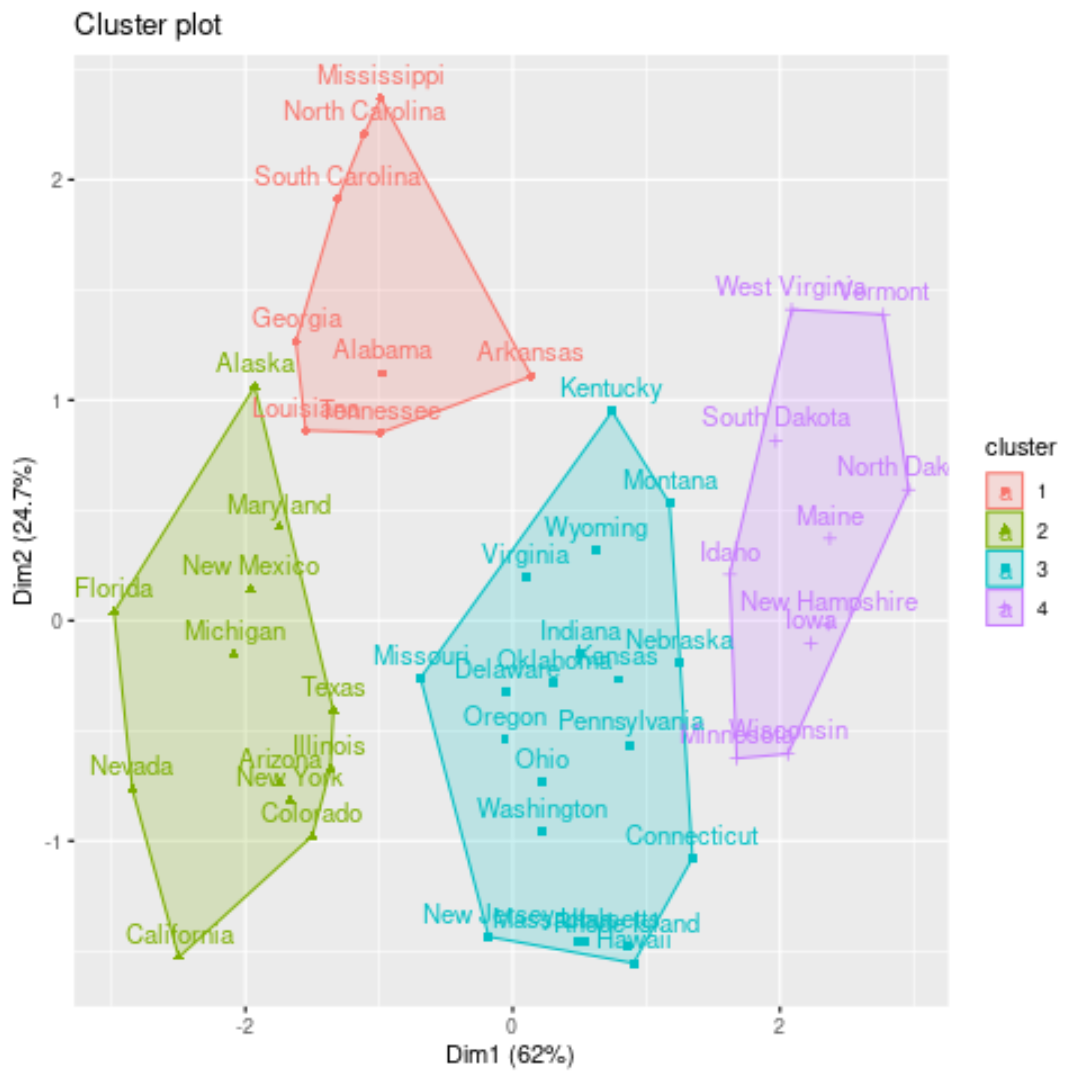
Ayrıca her bir durumun küme atamalarını orijinal veri kümesine ekleyebiliriz:

 #add cluster assignment to original data
final_data <- cbind(USArrests, cluster = kmed$cluster)

#view final data
head(final_data)

           Murder Assault UrbanPop Rape cluster
Alabama 13.2 236 58 21.2 1
Alaska 10.0 263 48 44.5 2
Arizona 8.1 294 80 31.0 2
Arkansas 8.8 190 50 19.5 1
California 9.0 276 91 40.6 2
Colorado 7.9 204 78 38.7 2

Bu örnekte kullanılan R kodunun tamamını burada bulabilirsiniz.