R'de teşhis grafikleri nasıl yorumlanır

Doğrusal regresyon modelleri, bir veya daha fazla yordayıcı değişken ile bir yanıt değişkeni arasındaki ilişkiyi tanımlamak için kullanılır.

Bununla birlikte, bir regresyon modeli yerleştirdikten sonra, model artıklarını analiz etmek ve üzerinde çalıştığımız belirli veriler için doğrusal bir modelin kullanıma uygun olduğundan emin olmak için teşhis grafikleri de oluşturmak iyi bir fikirdir.

Bu eğitimde, R’de belirli bir regresyon modeli için tanı grafiklerinin nasıl oluşturulacağı ve yorumlanacağı açıklanmaktadır.

Örnek: R’de tanılama grafikleri oluşturma ve yorumlama

Belirli bir sınıftaki öğrencilerin “sınav notlarını” tahmin etmek için “çalışılan saatleri” kullanarak basit bir doğrusal regresyon modeli uyguladığımızı varsayalım:

 #create data frame
df <- data. frame (hours=c(1, 1, 2, 2, 2, 3, 3, 4, 4, 4, 4, 5, 5, 6),
                 score=c(67, 65, 68, 77, 73, 79, 81, 88, 80, 67, 84, 93, 90, 91)) 

#fit linear regression model
model = lm(score ~ hours, data=df)

Bu regresyon modeli için dört tanısal grafik oluşturmak amacıylaplot () komutunu kullanabiliriz:

 #produce diagnostic plots for regression model
plot(model)

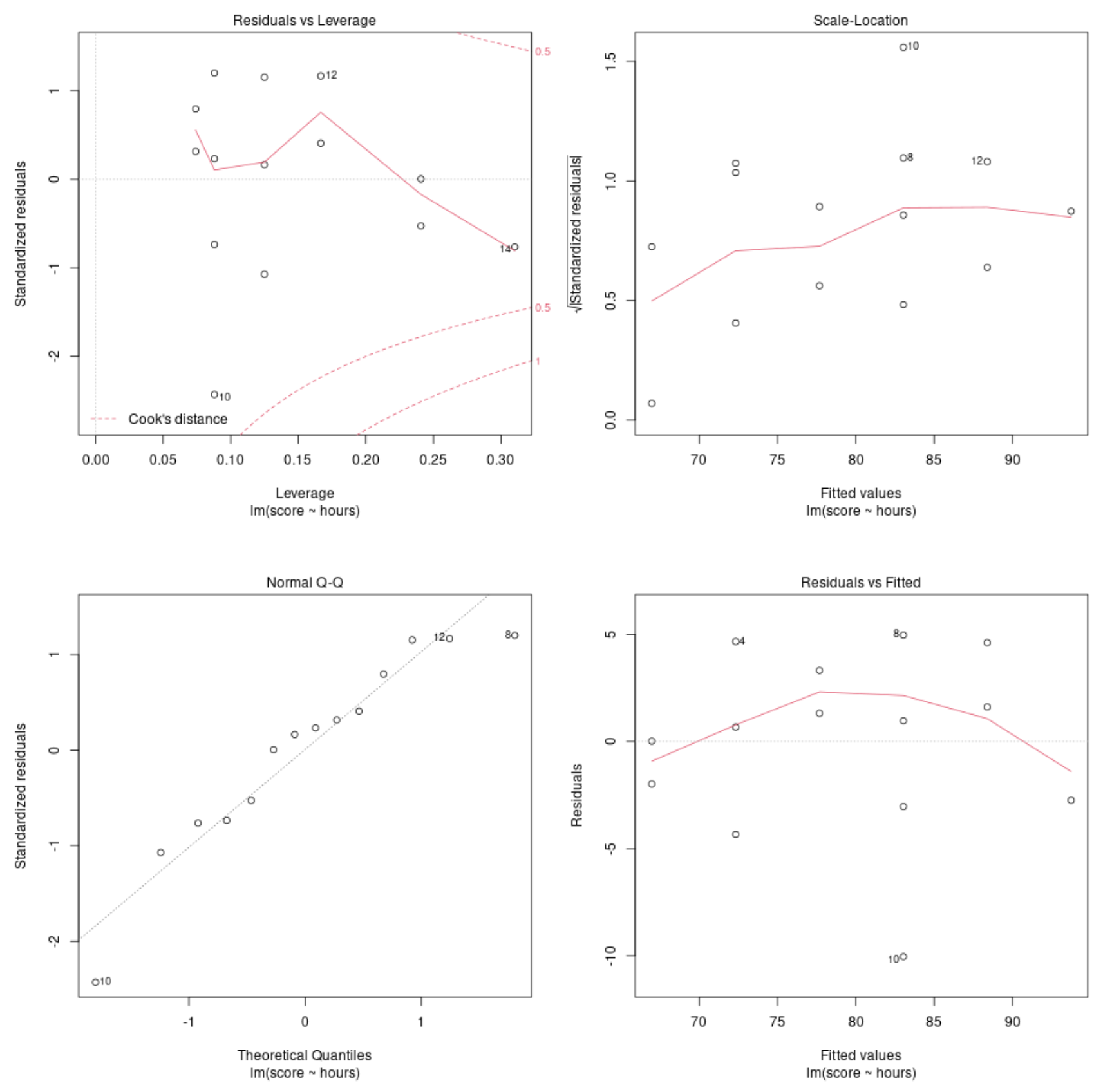
Teşhis Tablosu #1: Artıklar vs. Kaldıraç Grafiği

Bu grafik etkili gözlemleri tanımlamak için kullanılır. Bu grafikteki herhangi bir nokta Cook mesafesinin (noktalı çizgiler) dışında kalıyorsa, bu etkili bir gözlemdir.

Örneğimizde 10 numaralı gözlemin Pişirme mesafesi sınırına en yakın olduğunu ancak noktalı çizginin dışına çıkmadığını görebiliriz. Bu, veri setimizde aşırı etkili noktaların olmadığı anlamına gelir.

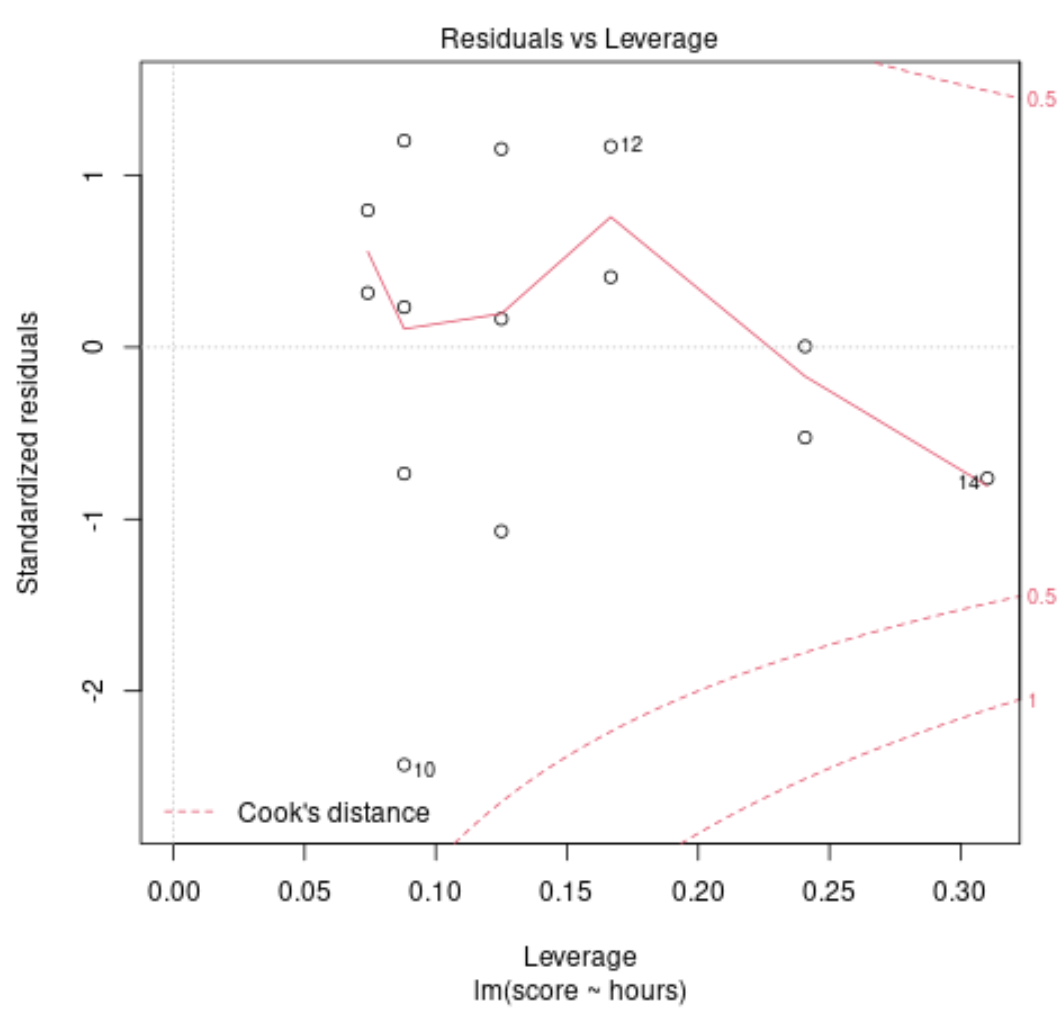
Teşhis Grafiği #2: Ölçek ve Konum Grafiği

Bu grafik, regresyon modelimizin kalıntıları arasındaki varyansın eşitliği (“homoskedasticity” olarak da adlandırılır) varsayımını doğrulamak için kullanılır. Eğer kırmızı çizgi grafikte yaklaşık olarak yatay ise, o zaman eşit varyans varsayımı muhtemelen karşılanmıştır.

Örneğimizde kırmızı çizginin çizim üzerinde tam olarak yatay olmadığını ancak hiçbir noktada çok fazla sapmadığını görebiliyoruz. Bu durumda muhtemelen eşit varyans varsayımının ihlal edilmediğini söyleyebiliriz.

İlgili: Regresyon Analizinde Heteroskedasticity’yi Anlamak

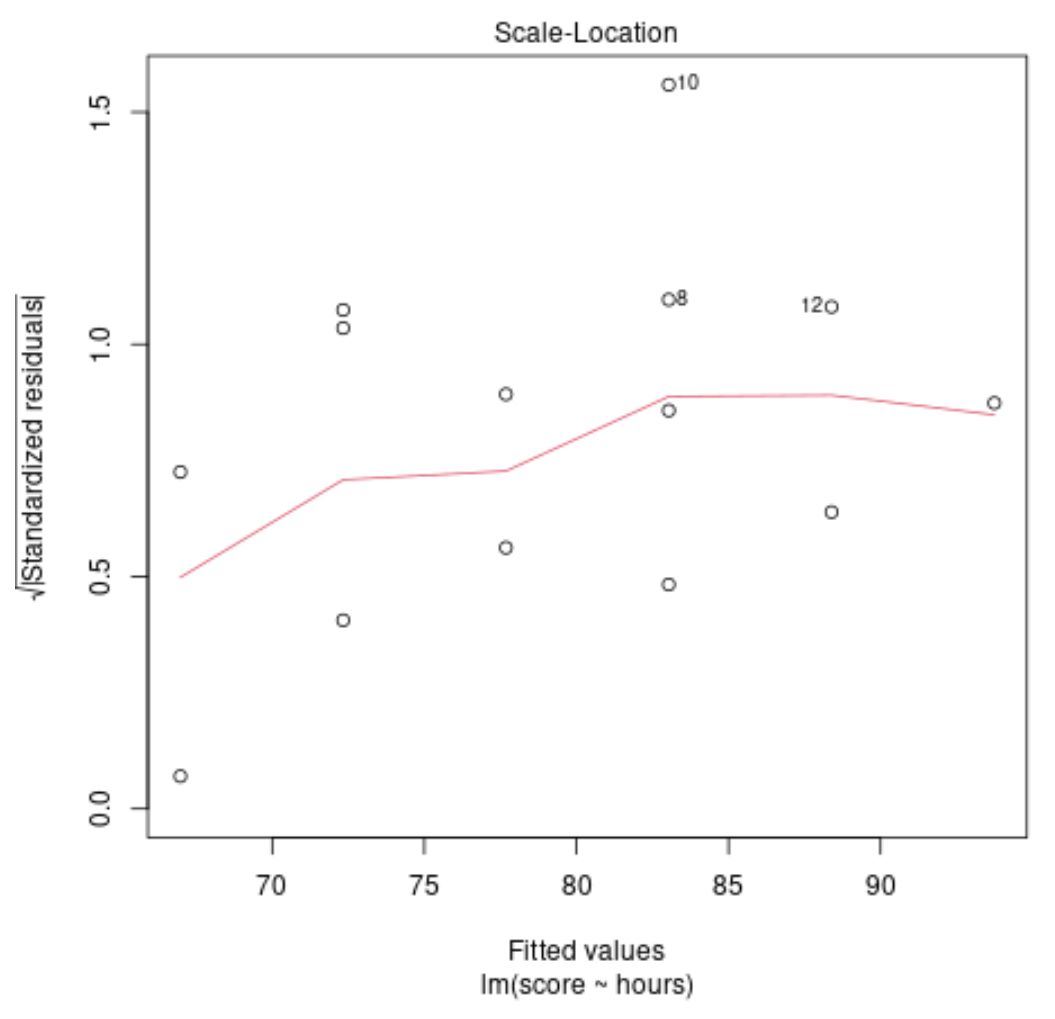
Tanısal iz #3: normal QQ izi

Bu grafik, regresyon modelinden elde edilen artıkların normal şekilde dağılıp dağılmadığını belirlemek için kullanılır. Bu grafikteki noktalar yaklaşık olarak düz bir çapraz çizgi boyunca yer alıyorsa, artıkların normal şekilde dağıldığını varsayabiliriz.

Örneğimizde noktaların kabaca çapraz düz çizgi boyunca uzandığını görebiliriz. 10 ve 8 numaralı gözlemler uçlarda çizgiden biraz sapmaktadır, ancak artıkların normal şekilde dağılmadığını beyan etmek için yeterli değildir.

Teşhis Planı #4: Kalıntılar vs. Düzeltilmiş Grafik

Bu grafik, artıkların doğrusal olmayan modeller sergileyip sergilemediğini belirlemek için kullanılır. Grafiğin ortasındaki kırmızı çizgi yaklaşık olarak yatay ise, artıkların doğrusal bir desen izlediğini varsayabiliriz.

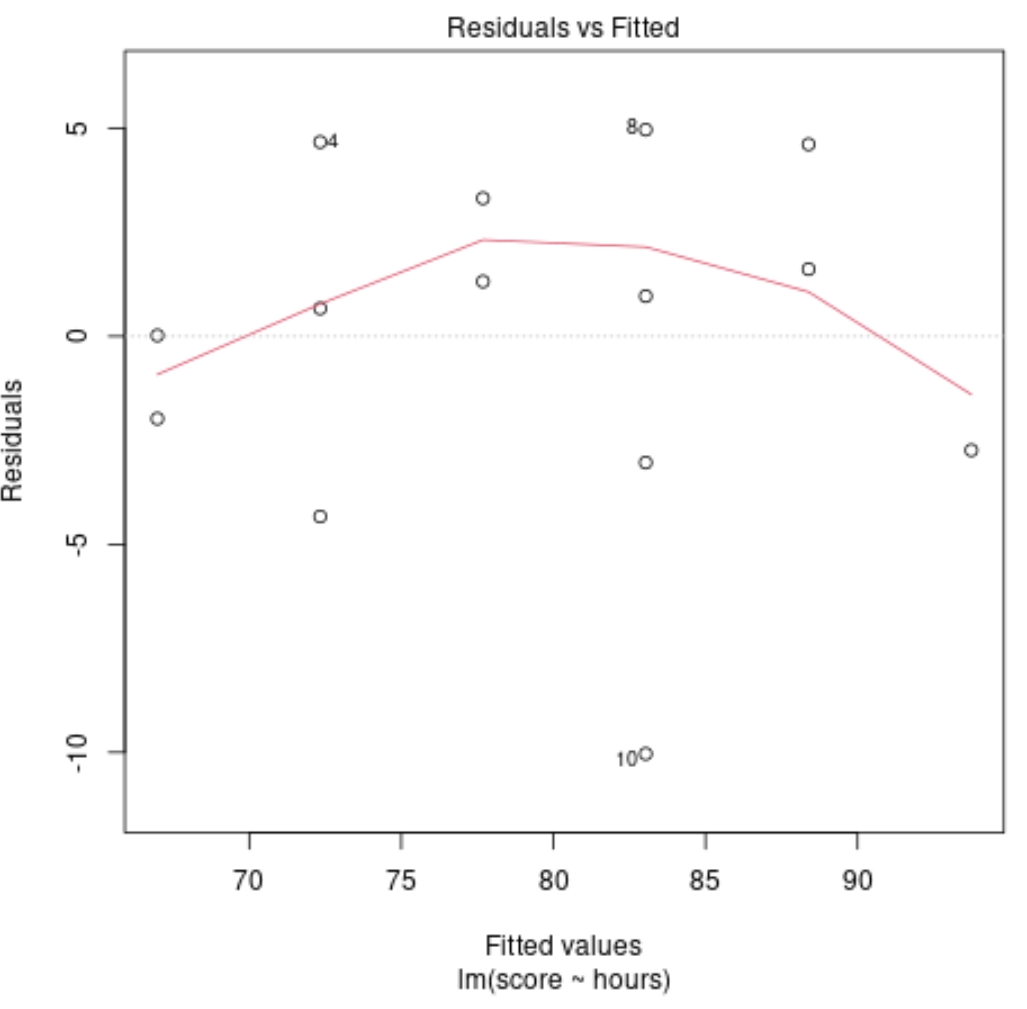
Örneğimizde, kırmızı çizginin mükemmel bir yatay çizgiden saptığını ancak önemli ölçüde sapmadığını görebiliriz. Muhtemelen artıkların kabaca doğrusal bir model izlediğini ve bu veri seti için doğrusal bir regresyon modelinin uygun olduğunu belirtiyoruz.

Ek kaynaklar

Doğrusal regresyonun dört varsayımı
İstatistiklerde artıklar nelerdir?
R’de artık arsa nasıl oluşturulur
Ölçek ve konum grafiği nasıl yorumlanır?