Regresyon eğiminin önemi nasıl test edilir?

Diyelim ki 12 farklı evin metrekaresini ve fiyatını gösteren aşağıdaki veri setine sahibiz:

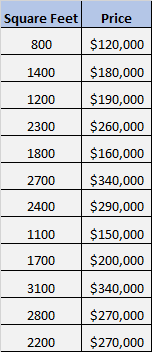
Metrekare ile fiyat arasında anlamlı bir ilişki olup olmadığını bilmek istiyoruz.

Verilerin neye benzediğine dair bir fikir edinmek için öncelikle x ekseninde fit kare ve y ekseninde fiyatın yer aldığı bir dağılım grafiği oluşturuyoruz:

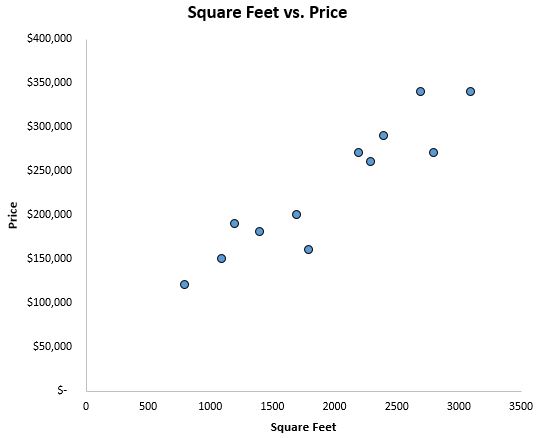
Metrekare ile fiyat arasında pozitif bir korelasyon olduğunu açıkça görebiliyoruz. Metrekare arttıkça evin fiyatı da artıyor.

Ancak metrekare ile fiyat arasında istatistiksel olarak anlamlı bir ilişki olup olmadığını anlamak için basit bir doğrusal regresyon yapmamız gerekiyor.

Bu nedenle, fit kareyi öngörü olarak ve fiyatı yanıt olarak kullanarak basit bir doğrusal regresyon çalıştırıyoruz ve aşağıdaki sonucu elde ediyoruz:

İster Excel’de, SPSS’de, R’de, isterse başka herhangi bir yazılımda basit bir doğrusal regresyon çalıştırıyor olun, yukarıda gösterilene benzer bir sonuç elde edeceksiniz.

Basit bir doğrusal regresyonun, dağılım grafiğimizdeki verilere en iyi “uyan” çizginin denklemi olan en iyi uyum çizgisini üreteceğini unutmayın. Bu en iyi uyum çizgisi şu şekilde tanımlanır:

ŷ = b ₀ + b ₁ x

burada ŷ yanıt değişkeninin tahmin edilen değeridir, b ₀ kesişme noktasıdır, b ₁ regresyon katsayısıdır ve x yordayıcı değişkenin değeridir.

b ₀ değeri 47588,70 olan orijin katsayısı ile verilmektedir.

b _1’in değeri, 93,57 olan Feet Kare tahmin değişkeninin katsayısı ile verilmektedir .

Yani bu örnekte en uygun doğru ŷ = 47588,70+ 93,57x’tir.

Bu en uygun çizgiyi nasıl yorumlayacağınız aşağıda açıklanmıştır:

• b ₀ : Metrekare değeri sıfır olduğunda beklenen ortalama fiyat değeri 47.588,70$ olur. (Bu durumda, bir evin hiçbir zaman sıfır metrekaresi olamayacağından, kesişimi yorumlamak pek mantıklı değildir)
• b ₁ : Her ilave metrekare için fiyatta beklenen ortalama artış 93,57$’dır.

Artık her ilave metrekare için fiyatta beklenen ortalama artışın 93,57 dolar olduğunu biliyoruz.

Bu artışın istatistiksel olarak anlamlı olup olmadığını anlamak için B ₁ için bir hipotez testi yapmamız veya B ₁ için bir güven aralığı oluşturmamız gerekiyor.

Not : Bir hipotez testi ve güven aralığı her zaman aynı sonuçları verecektir.

Regresyon eğimi için güven aralığının oluşturulması

Bir regresyon eğimine ilişkin güven aralığı oluşturmak için aşağıdaki formülü kullanırız:

Güven aralığı = b ₁ +/- (t _{1-∝/2, n-2} ) * (b _1’in standart hatası)

Altın:

• b ₁ regresyon sonucunda verilen eğim katsayısıdır
• (t _{1-∝/2, n-2} ), n-2 serbestlik derecesine sahip 1-∝ güven düzeyi için kritik t değeridir; burada n , veri setimizdeki toplam gözlem sayısıdır
• (b _1’in standart hatası), regresyon sonucunda verilen b _1’in standart hatasıdır

Örneğimiz için, B ₁ için %95’lik bir güven aralığının nasıl oluşturulacağı aşağıda açıklanmıştır:

• b _1, regresyon çıktısından 93,57’dir.
• %95 güven aralığı kullandığımız için ∝ = 0,05 ve n-2 = 12-2 = 10, yani t _{0,975, 10} t dağılım tablosuna göre 2,228 olur
• ( _b1’in standart hatası) regresyon çıktısından 11,45’tir

Dolayısıyla B ₁ için %95 güven aralığımız şu şekildedir:

93,57 +/- (2,228) * (11,45) = (68,06, 119,08)

Bu, her ilave metrekare için gerçek ortalama fiyat artışının 68,06 ile 119,08 dolar arasında olacağından %95 emin olduğumuz anlamına geliyor.

0 doların bu aralıkta olmadığını, dolayısıyla metrekare ile fiyat arasındaki ilişkinin %95 güven düzeyinde istatistiksel olarak anlamlı olduğunu unutmayın.

Regresyon eğimi için hipotez testinin yapılması

Bir regresyon eğimine yönelik bir hipotez testi gerçekleştirmek için herhangi bir hipotez testi için beş standart adımı takip ederiz:

Adım 1. Hipotezleri belirtin.

Sıfır hipotezi (H0): B ₁ = 0

Alternatif hipotez: (Ha): B ₁ ≠ 0

Adım 2. Kullanılacak bir önem düzeyi belirleyin.

Önceki örnekte %95’lik bir güven aralığı oluşturduğumuzdan, burada eşdeğer yaklaşımı kullanacağız ve 0,05 anlamlılık düzeyini kullanmayı seçeceğiz.

Adım 3. Test istatistiğini ve karşılık gelen p değerini bulun.

Bu durumda test istatistiği t = b ₁ katsayısı / b _1’in n-2 serbestlik derecesi ile standart hatasıdır. Bu değerleri regresyon sonucundan bulabiliriz:

Böylece test istatistiği t = 92,89 / 13,88 = 6,69 olur.

10 serbestlik derecesi ve iki kuyruklu test ile 6,69 puana sahip T puanı – P değeri hesaplayıcısı kullanıldığında p değeri = 0,000 olur.

Adım 4. Boş hipotezi reddedin veya reddetmeyin.

P değeri 0,05 anlamlılık seviyemizin altında olduğundan sıfır hipotezini reddediyoruz.

Adım 5. Sonuçları yorumlayın.

Sıfır hipotezini reddettiğimiz için, her ilave metrekare için fiyattaki gerçek ortalama artışın sıfır olmadığını söyleyecek yeterli kanıtımız var.