Regresyon eğiminin standart hatasını anlamak

Bir regresyon eğiminin standart hatası, bir regresyon eğiminin tahmin edilmesindeki “belirsizliği” ölçmenin bir yoludur.

Aşağıdaki şekilde hesaplanır:

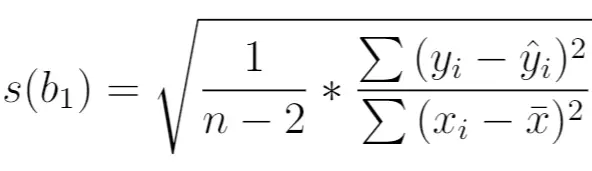
Altın:

• n : toplam örneklem büyüklüğü
• y _i : yanıt değişkeninin gerçek değeri
• ŷ _i : yanıt değişkeninin tahmin edilen değeri
• x _i : tahmin değişkeninin gerçek değeri
• x̄ : tahmin değişkeninin ortalama değeri

Standart hata ne kadar küçük olursa, regresyon eğimi için katsayı tahmini etrafındaki değişkenlik de o kadar düşük olur.

Regresyon eğiminin standart hatası, çoğu istatistiksel yazılımın regresyon çıktısında bir “standart hata” sütununda görüntülenecektir:

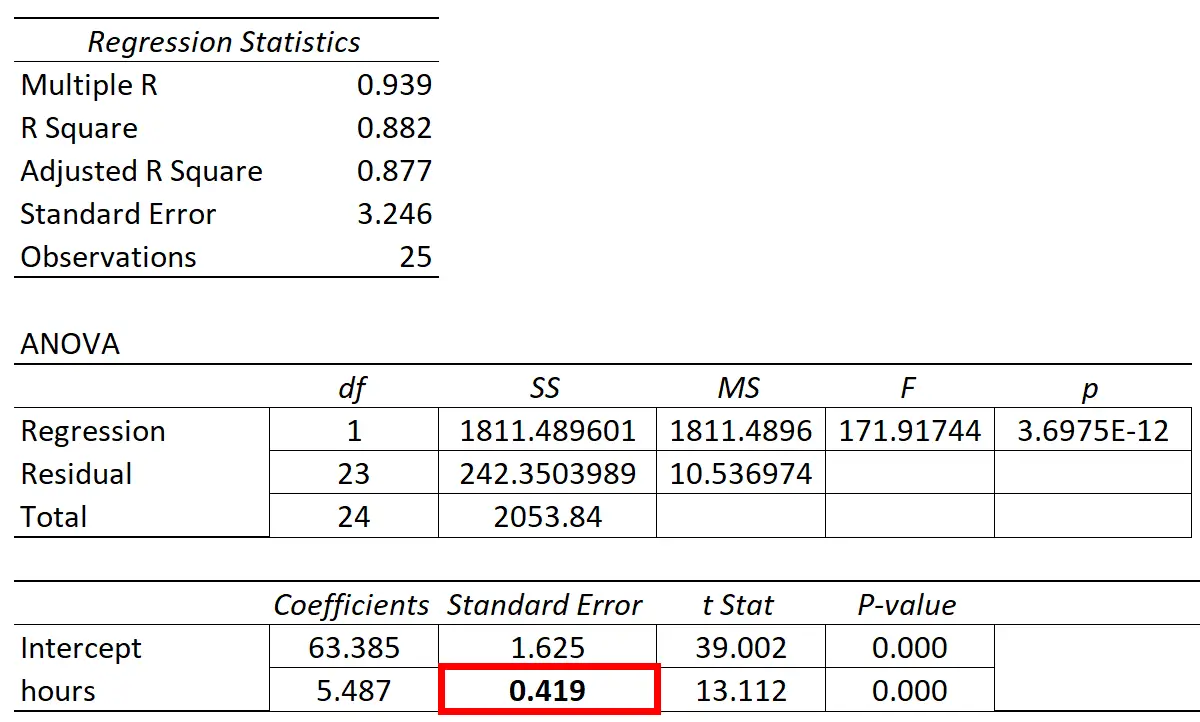
Aşağıdaki örnekler, bir regresyon eğiminin standart hatasının iki farklı senaryoda nasıl yorumlanacağını göstermektedir.

Örnek 1: Regresyon Eğiminin Küçük Standart Hatasını Yorumlama

Bir profesörün, ders saati sayısı ile sınıfındaki öğrencilerin final sınav notları arasındaki ilişkiyi anlamak istediğini varsayalım.

25 öğrenciden veri toplar ve aşağıdaki dağılım grafiğini oluşturur:

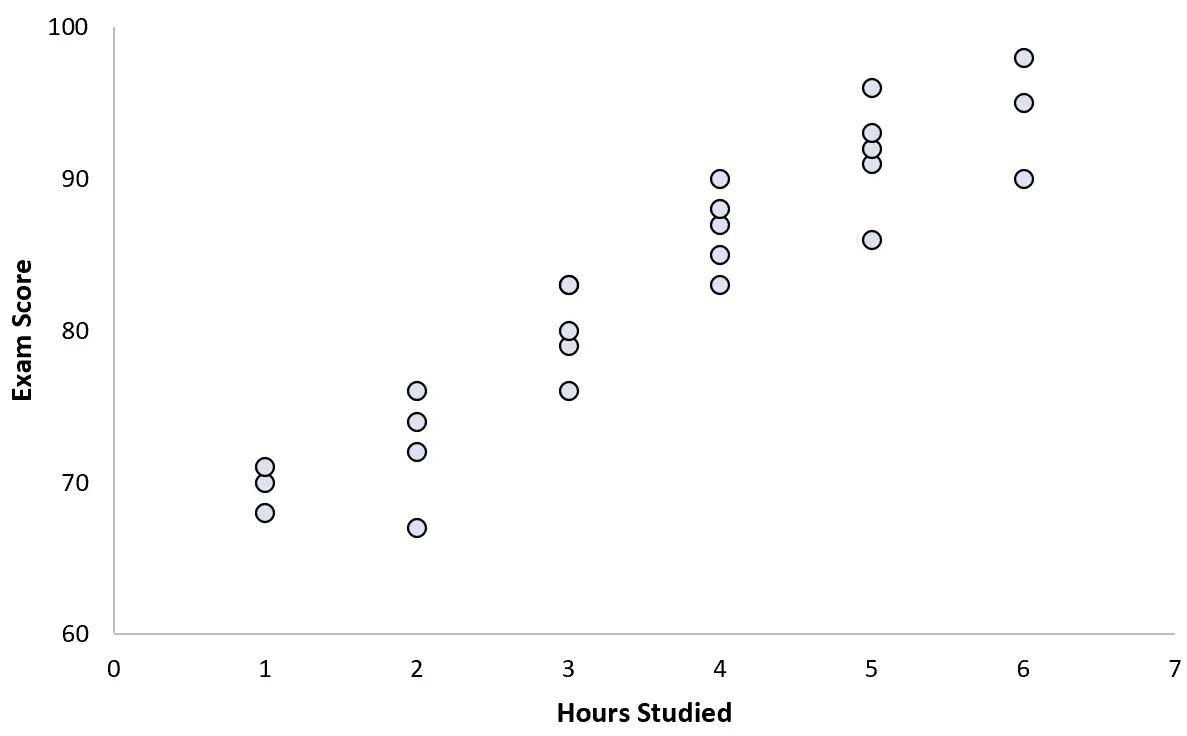
İki değişken arasında açıkça pozitif bir ilişki vardır. Çalışılan saat sayısı arttıkça sınav puanı da oldukça öngörülebilir bir oranda artmaktadır.

Daha sonra yordayıcı değişken olarak çalışılan saatleri ve yanıt değişkeni olarak final sınav notunu kullanarak basit bir doğrusal regresyon modeli uyguladı.

Aşağıdaki tabloda regresyon sonuçları gösterilmektedir:

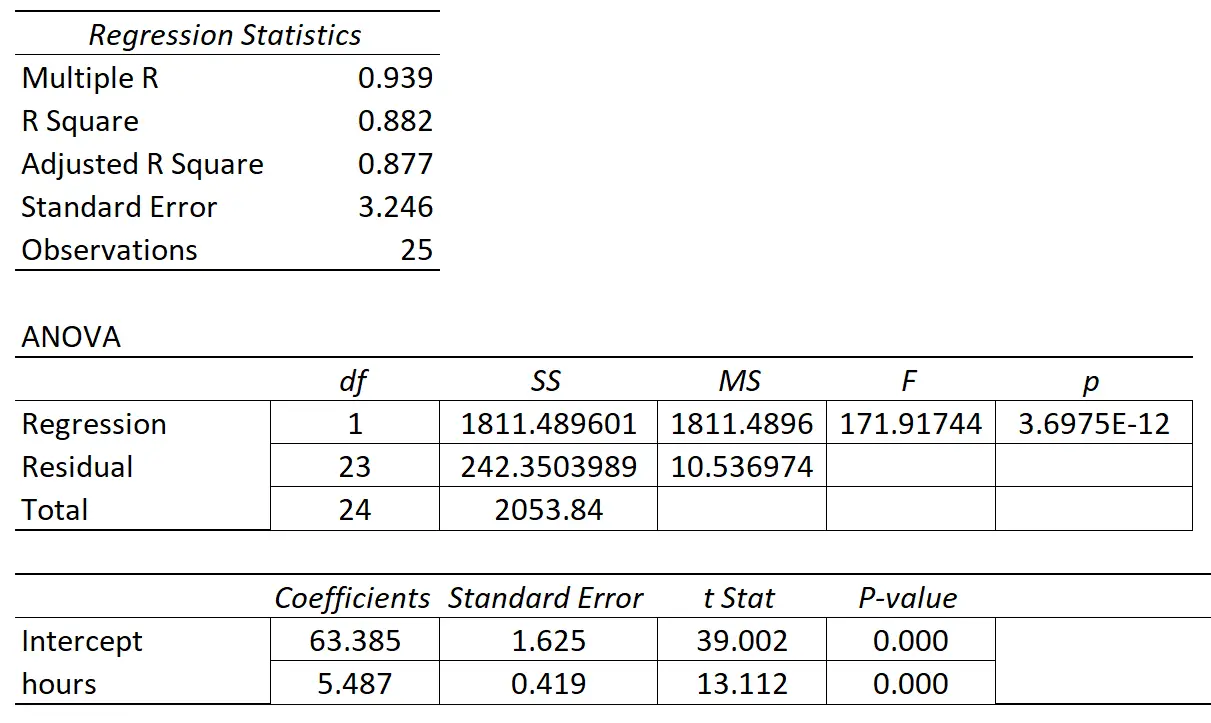
Yordayıcı değişken “çalışma saati”nin katsayısı 5.487’dir. Bu bize, çalışılan her ek saatin sınav puanında ortalama 5.487 puanlık bir artışla ilişkili olduğunu söylüyor.

Standart hata 0,419’dur ve bu, regresyon eğimi için bu tahmin etrafındaki değişkenliğin bir ölçüsünü temsil eder.

Bu değeri, “çalışılan saat” yordayıcı değişkenine ilişkin t-istatistiğini hesaplamak için kullanabiliriz:

• t istatistiği = katsayı tahmini / standart hata
• t-istatistiği = 5,487 / 0,419
• t-istatistiği = 13.112

Bu test istatistiğine karşılık gelen p değeri 0,000 olup, “çalışılan saat” ile final sınav notu arasında istatistiksel olarak anlamlı bir ilişkinin olduğunu göstermektedir.

Regresyon eğiminin standart hatası, regresyon eğiminin katsayı tahminine kıyasla küçük olduğundan, yordayıcı değişken istatistiksel olarak anlamlıydı.

Örnek 2: Bir Regresyon Eğiminin Büyük Standart Hatasının Yorumlanması

Başka bir profesörün, kendi sınıfındaki öğrencilerin ders saatleriyle final sınav notları arasındaki ilişkiyi anlamak istediğini varsayalım.

25 öğrenciden veri topluyor ve aşağıdaki dağılım grafiğini oluşturuyor:

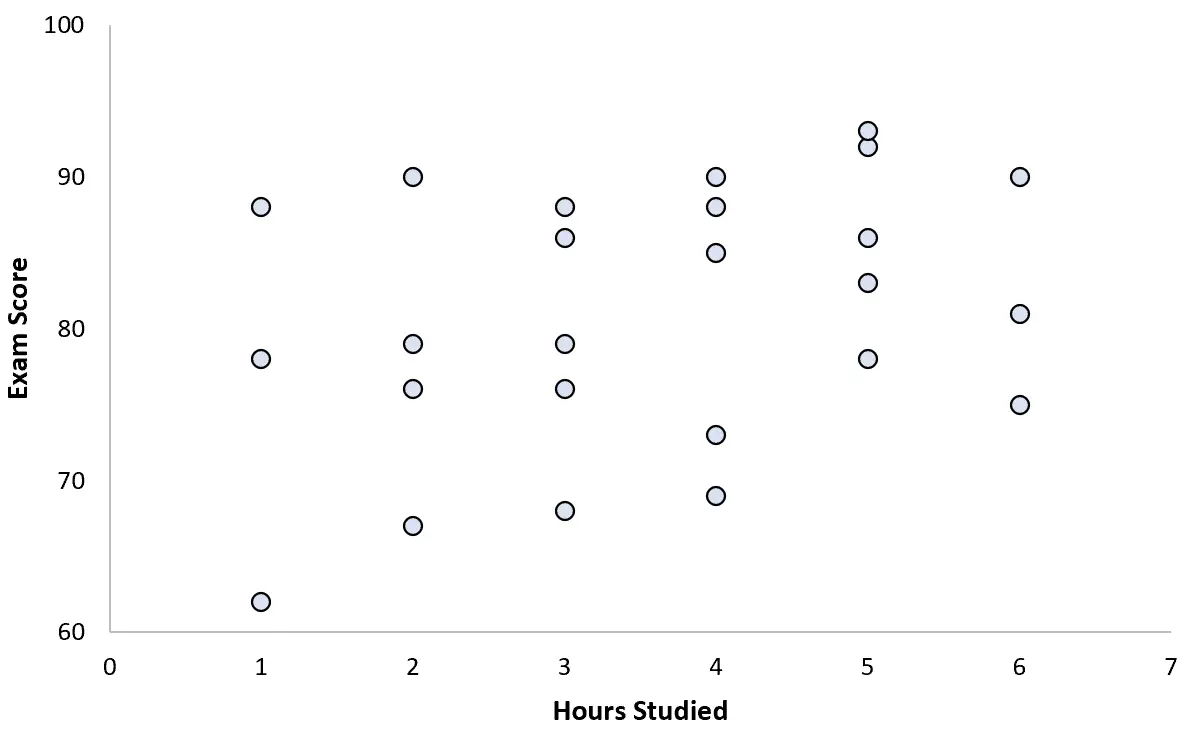
İki değişken arasında hafif pozitif bir ilişki olduğu görülmektedir. Çalışma saati arttıkça sınav puanı da genel olarak artıyor ancak öngörülebilir bir oranda değil.

Profesörün daha sonra yordayıcı değişken olarak çalışılan saatleri ve yanıt değişkeni olarak final sınav notunu kullanarak basit bir doğrusal regresyon modeline uyduğunu varsayalım.

Aşağıdaki tabloda regresyon sonuçları gösterilmektedir:

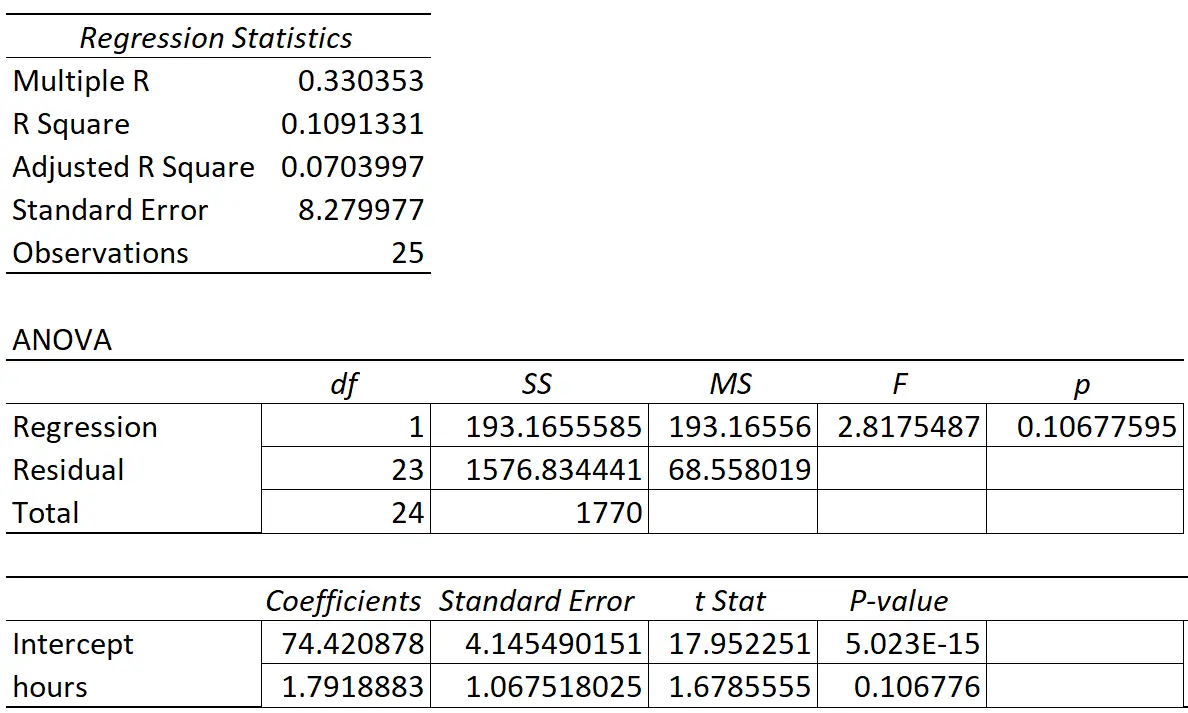
Yordayıcı değişken “çalışma saati”nin katsayısı 1,7919’dur. Bu bize, çalışılan her ek saatin sınav puanında ortalama 1,7919’luk bir artışla ilişkili olduğunu söylüyor.

Standart hata 1,0675’tir ve bu, regresyon eğimi için bu tahmin etrafındaki değişkenliğin bir ölçüsüdür.

Bu değeri, “çalışılan saat” yordayıcı değişkenine ilişkin t-istatistiğini hesaplamak için kullanabiliriz:

• t istatistiği = katsayı tahmini / standart hata
• t-istatistiği = 1,7919 / 1,0675
• t-istatistiği = 1,678

Bu test istatistiğine karşılık gelen p değeri 0,107’dir. Bu p değeri 0,05’ten küçük olmadığı için “çalışılan saat” ile final sınav notu arasında istatistiksel olarak anlamlı bir ilişkinin olmadığı anlaşılmaktadır.

Regresyon eğiminin standart hatası, regresyon eğiminin katsayı tahminine göre büyük olduğundan, yordayıcı değişken istatistiksel olarak anlamlı değildi .

Ek kaynaklar

Basit Doğrusal Regresyona Giriş
Çoklu Doğrusal Regresyona Giriş
Regresyon Tablosu Nasıl Okunmalı ve Yorumlanmalı