Regresyon hattı

İle Dr.benjamin anderson Ağustos 2, 2023 İstatistik 0 Yorum

Bu makale istatistikte regresyon çizgisinin ne olduğunu açıklamaktadır. Böylece, iki değişken arasındaki regresyon çizgisini nasıl hesaplayacağınızı, çözülmüş bir alıştırmayı ve ek olarak herhangi bir veri örneği için regresyon çizgisini hesaplamak için çevrimiçi bir hesap makinesini bulacaksınız.

Regresyon çizgisi nedir?

İstatistikte regresyon çizgisi , basit bir doğrusal regresyon modelinden elde edilen çizgidir. Daha doğrusu, regresyon çizgisi bir dağılım grafiğine en iyi uyan çizgidir ve dolayısıyla bir dizi istatistiksel veriyi en iyi şekilde tanımlar.

Böylece regresyon çizgisi denklemi, bir veri kümesinin bağımsız değişkeni X ile bağımlı değişkeni Y’yi matematiksel olarak ilişkilendirir. Regresyon çizgisi genel olarak her bir gözlemin değerini kesin olarak belirleme yeteneğine sahip olmasa da, onun değerine ilişkin bir yaklaşım sağlayabilir.

Önceki grafikte görebileceğiniz gibi regresyon çizgisi, bir veri setinin eğilimini ve bağımsız değişken ile bağımlı değişken arasında ne tür bir ilişkinin bulunduğunu görmemize yardımcı olur. Aşağıda regresyon çizgisinin uygulamalarına bakacağız.

Regresyon çizgisi formülü

Artık regresyon çizgisinin tanımını bildiğimize göre, doğrusal regresyon modelinin çizgisinin denkleminin nasıl hesaplanacağını görelim.

Herhangi bir doğru gibi, regresyon çizgisinin denklemi de bir sabit (b ₀ ) ve bir eğimden (b ₁ ) oluşur:

$y=b_0+b_1x$

Böylece doğrusal regresyon çizgisinin katsayılarını hesaplamaya yönelik formüller aşağıdaki gibidir:

$\begin{array}{c}b_1=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{\displaystyle \sum_{i=1}^n (x_i-\overline{x})^2}\\[12ex]b_0=\overline{y}-b_1\overline{x}\end{array}$

Altın:

$b_0$

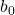
regresyon çizgisinin sabitidir.
$b_1$

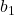
regresyon çizgisinin eğimidir.
$x_i$

i verisinin bağımsız değişkeni X’in değeridir.
$y_i$

i verisinin bağımlı değişkeni Y’nin değeridir.
$\overline{x}$

bağımsız değişkenin değerlerinin ortalamasıdır
$\overline{y}$

bağımlı değişken Y’nin değerlerinin ortalamasıdır.

👉Herhangi bir veri seti için regresyon doğrusunu hesaplamak için aşağıdaki hesap makinesini kullanabilirsiniz.

Regresyon çizgisinin somut örneği

Regresyon çizgisi kavramını daha ayrıntılı olarak keşfetmek için aşağıda bir regresyon çizgisinin nasıl oluşturulacağına dair çalışılmış bir örnek verilmiştir.

İstatistik sınavına girdikten sonra beş öğrenciye sınava kaç saat ders çalıştıkları soruldu, veriler aşağıdaki tabloda gösterildi. Çalışma saatlerini alınan notla doğrusal olarak ilişkilendirmek için toplanan istatistiksel verilerden regresyon çizgisini hesaplayın. Daha sonra 8 saat ders çalışan öğrencinin hangi notu alacağını belirleyin.

Örnek verilere ait regresyon doğrusunu bulmak için denklemin b ₀ ve b ₁ katsayılarını belirlememiz ve bunun için yukarıdaki bölümde görülen formülleri kullanmamız gerekir.

Ancak doğrusal regresyon çizgisi formüllerini uygulamak için öncelikle bağımsız değişkenin ortalamasını ve bağımlı değişkenin ortalamasını hesaplamamız gerekir:

$\begin{array}{c}\overline{x}=\cfrac{11+5+10+12+7}{5}=9\\[4ex]\overline{y}=\cfrac{7+4+5+8+6}{5}=6\end{array}$

Artık değişkenlerin ortalamasını bildiğimize göre, ilgili formülü kullanarak modelin b ₁ katsayısını hesaplıyoruz:

$\begin{array}{c}b_1=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{\displaystyle \sum_{i=1}^n (x_i-\overline{x})^2}\\[10ex] b_1=\cfrac{\begin{array}{c}(11-9)(7-6)+(5-9)(4-6)+(10-9)(5-6)+\\+(12-9)(8-6)+(7-9)(6-6)\end{array}}{(11-9)^2+(5-9)^2+(10-9)^2+(12-9)^2+(7-9)^2}\\[6ex]b_1=0,4412\end{array}$

Son olarak, ilgili formülü kullanarak modelin b ₀ katsayısını hesaplıyoruz:

$\begin{array}{l}b_0=\overline{y}-b_1\overline{x}\\[3ex]b_0=6-0,4412\cdot 9 \\[3ex]b_0=2,0294\end{array}$

Kısaca problemin doğrusal regresyon çizgisinin denklemi aşağıdaki gibidir:

$y=2,0294+0,4412x$

Aşağıda örnek verilerin grafiksel gösterimini ve basit doğrusal regresyon modelinin düz çizgisini görebilirsiniz:

Regresyon doğrusunu hesapladıktan sonra 8 saat eğitim alan bir öğrencinin alacağı notu tahmin etmek için bu değeri elde edilen regresyon doğrusu denkleminde yerine koymanız yeterlidir:

$y=2,0294+0,4412\cdot 8=5,56$

Böylece gerçekleştirilen doğrusal regresyon modeline göre bir öğrenci sekiz saat ders çalışırsa sınavdan 5,56 puan alacaktır.

Regresyon çizgisi ne için kullanılır?

Temel olarak regresyon çizgisinin iki kullanımı vardır: Regresyon çizgisi iki değişken arasında ne tür bir ilişkinin bulunduğunu belirlemek için kullanılır ve diğer yandan regresyon çizgisi aynı zamanda yeni bir gözlemin değeri hakkında tahminde bulunmanıza da olanak tanır.

Regresyon çizgisinin eğimi bize bağımsız değişken ile bağımlı değişken arasındaki ilişkinin nasıl olduğunu anlatır. Eğimin pozitif olması bağımlı değişkenin bağımsız değişkenle doğru orantılı olduğu, eğimin negatif olması ise değişkenlerin ters orantılı olduğu anlamına gelir. Son olarak eğim katsayısının sıfıra çok yakın olması iki değişken arasındaki ilişkinin çok zayıf olduğu anlamına gelir.

Ayrıca regresyon çizgisinin denklemi biliniyorsa yukarıdaki örnekte yaptığımız gibi bağımsız değişkenin yeni değeri için bağımlı değişkenin değeri tahmin edilebilir. Dolayısıyla regresyon çizgisi ne kadar iyi adapte edilirse o kadar iyi tahminlerde bulunulacaktır.

Regresyon çizgisi hesaplayıcısı

İki değişken arasındaki regresyon çizgisini hesaplamak için aşağıdaki hesap makinesine bir veri örneği girin. Veri çiftlerini ayırmanız gerekir, böylece ilk kutuda yalnızca bağımsız değişken X’in değerleri bulunur ve ikinci kutuda yalnızca bağımlı değişken Y’nin değerleri bulunur.

Veriler bir boşlukla ayrılmalı ve ondalık ayırıcı olarak nokta kullanılarak girilmelidir.

yazar hakkında

Dr.benjamin anderson

Merhaba, ben Benjamin, emekli bir istatistik profesörü ve Statorials öğretmenine dönüştüm. İstatistik alanındaki kapsamlı deneyimim ve uzmanlığımla, öğrencilerimi Statorials aracılığıyla güçlendirmek için bilgilerimi paylaşmaya can atıyorum. Daha fazlasını bil