Ridge & lasso regresyon ne zaman kullanılır?
Sıradan çoklu doğrusal regresyonda , formun bir modeline uyacak şekilde bir dizi p tahmin değişkeni ve bir yanıt değişkeni kullanırız:
Y = β 0 + β 1 X 1 + β 2 X 2 + … + β p
β 0 , β 1 , B 2 , …, β p değerleri, artıkların karelerinin toplamını (RSS) en aza indiren en küçük kareler yöntemi kullanılarak seçilir:
RSS = Σ(y ben – ŷ ben ) 2
Altın:
- Σ : “Toplam” anlamına gelen bir sembol
- y i : i’inci gözlem için gerçek yanıt değeri
- ŷ i : i’inci gözlem için tahmin edilen yanıt değeri
Regresyonda çoklu bağlantı sorunu
Çoklu doğrusal regresyonda pratikte sıklıkla ortaya çıkan bir sorun, çoklu doğrusallıktır ; yani iki veya daha fazla yordayıcı değişken birbiriyle yüksek düzeyde korelasyona sahip olduğunda, regresyon modelinde benzersiz veya bağımsız bilgi sağlayamazlar.
Bu, model katsayı tahminlerini güvenilmez hale getirebilir ve yüksek varyans sergileyebilir. Yani model daha önce hiç görmediği yeni bir veri setine uygulandığında muhtemelen düşük performans gösterecektir.
Çoklu bağlantıdan kaçınma: Ridge & Lasso regresyonu
Bu çoklu bağlantı problemini aşmak için kullanabileceğimiz iki yöntem ridge regresyonu ve kement regresyonudur .
Ridge regresyonu aşağıdakileri en aza indirmeyi amaçlamaktadır:
- RSS + λΣβ j 2
Kement regresyonu aşağıdakileri en aza indirmeyi amaçlar:
- RSS + λΣ|β j |
Her iki denklemde de ikinci terime çekilme cezası denir.
λ = 0 olduğunda, bu ceza teriminin hiçbir etkisi yoktur ve sırt regresyonu ve kement regresyonu, en küçük kareler ile aynı katsayı tahminlerini üretir.
Ancak λ sonsuza yaklaştıkça büzülme cezası daha etkili hale gelir ve modele aktarılamayan tahmin değişkenleri sıfıra doğru azalır.
Lasso regresyonunda λ yeterince büyük olduğunda bazı katsayıların tamamen sıfır olması mümkündür.
Ridge & Lasso Regresyonunun Avantajları ve Dezavantajları
Ridge ve Lasso regresyonunun en küçük kareler regresyonuna göre avantajı önyargı-varyans değiş tokuşudur .
Ortalama Karesel Hatanın (MSE) belirli bir modelin doğruluğunu ölçmek için kullanabileceğimiz bir ölçüm olduğunu ve şu şekilde hesaplandığını hatırlayın:
MSE = Var( f̂( x 0 )) + [Önyargı( f̂( x 0 ))] 2 + Var(ε)
MSE = Varyans + Önyargı 2 + İndirgenemez hata
Ridge Regression ve Lasso Regression’ın temel fikri, varyansın önemli ölçüde azaltılabilmesi ve böylece daha düşük bir genel MSE’ye yol açabilmesi için küçük bir önyargı eklemektir.
Bunu açıklamak için aşağıdaki grafiği inceleyin:
λ arttıkça sapmadaki çok küçük bir artışla varyansın önemli ölçüde azaldığını unutmayın. Ancak belirli bir noktadan sonra varyans daha yavaş azalır ve katsayılardaki azalma onların önemli ölçüde eksik tahmin edilmesine yol açar, bu da yanlılığın keskin bir şekilde artmasına neden olur.
Grafikten, λ için önyargı ve varyans arasında optimal bir denge sağlayan bir değer seçtiğimizde testin MSE’sinin en düşük olduğunu görebiliriz.
λ = 0 olduğunda, kement regresyonundaki ceza teriminin hiçbir etkisi yoktur ve bu nedenle en küçük kareler ile aynı katsayı tahminlerini üretir. Ancak λ’yı belirli bir noktaya artırarak testin genel MSE’sini azaltabiliriz.
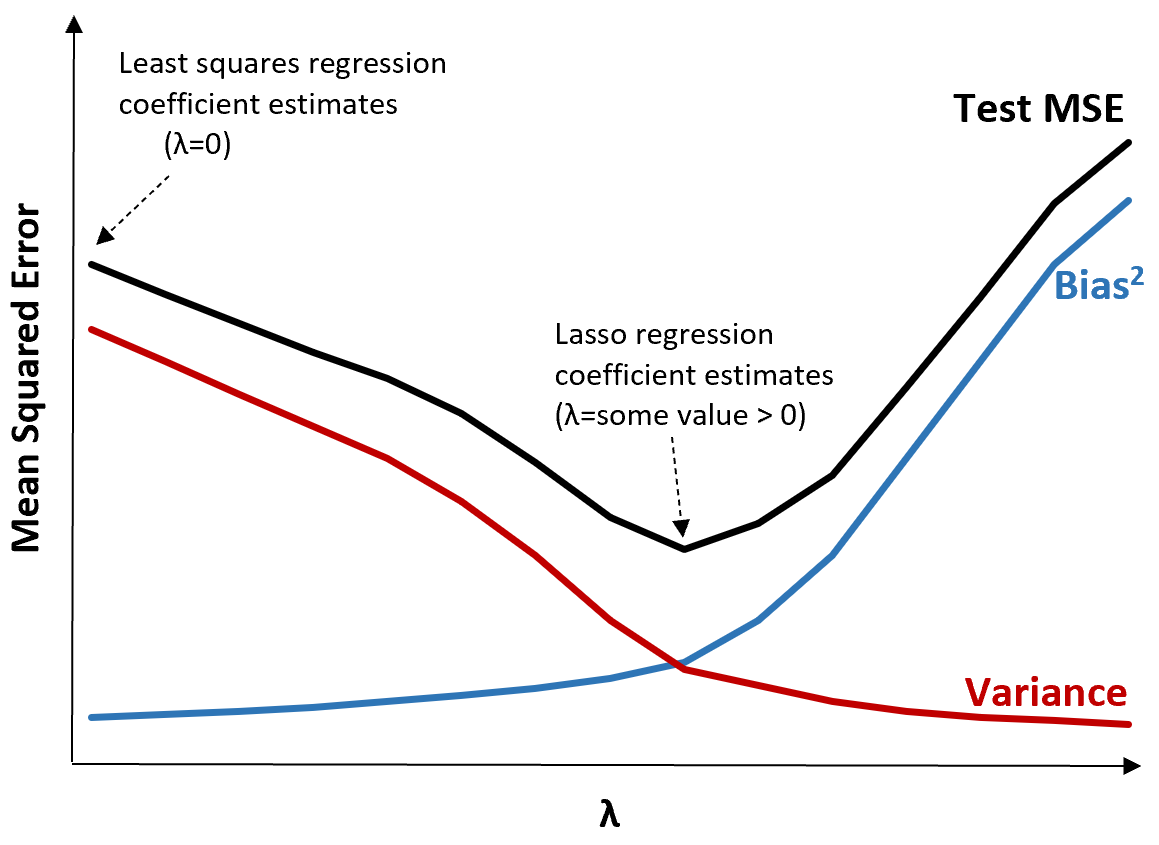
Bu, sırt ve kement regresyonuyla model uydurmanın, en küçük kareler regresyonuyla model uydurmaya göre potansiyel olarak daha küçük test hataları üretebileceği anlamına gelir.
Ridge ve Lasso regresyonunun dezavantajı , katsayıların sıfıra yaklaştıkça son modelde yorumlanmasının zorlaşmasıdır.
Bu nedenle, çıkarım yerine tahmin yeteneğini optimize etmek istediğinizde Ridge ve Lasso regresyonu kullanılmalıdır.
Ridge vs. Kement Regresyon: Her Biri Ne Zaman Kullanılmalı
L asso regresyonu ve ridge regresyonu düzenlileştirme yöntemleri olarak bilinir, çünkü her ikisi de artık kareler toplamını (RSS) ve belirli bir ceza terimini en aza indirmeye çalışır.
Başka bir deyişle, model katsayılarının tahminlerini kısıtlar veya düzenlerler .
Bu doğal olarak şu soruyu gündeme getiriyor: Sırt regresyonu mu yoksa kement regresyonu mu daha iyi?
Yalnızca az sayıda öngörücü değişkenin anlamlı olduğu durumlarda, kement regresyonu daha iyi çalışma eğilimindedir çünkü önemsiz değişkenleri tamamen sıfıra indirebilir ve bunları modelden çıkarabilir.
Bununla birlikte, birçok yordayıcı değişken modelde anlamlı olduğunda ve katsayıları yaklaşık olarak eşit olduğunda, ridge regresyonu daha iyi çalışma eğilimindedir çünkü tüm yordayıcıları modelde tutar.
Tahmin yapmak için hangi modelin en iyi olduğunu belirlemek için genellikle k-katlı çapraz doğrulama gerçekleştiririz ve en düşük test kök ortalama kare hatasını üreten modeli seçeriz.
Ek kaynaklar
Aşağıdaki eğitimler Ridge Regression ve Lasso Regression’a giriş sağlar:
Aşağıdaki eğitimlerde R ve Python’da her iki regresyon türünün nasıl gerçekleştirileceği açıklanmaktadır:
yazar hakkında
Dr.benjamin anderson
Merhaba, ben Benjamin, emekli bir istatistik profesörü ve Statorials öğretmenine dönüştüm. İstatistik alanındaki kapsamlı deneyimim ve uzmanlığımla, öğrencilerimi Statorials aracılığıyla güçlendirmek için bilgilerimi paylaşmaya can atıyorum. Daha fazlasını bil