Kök ortalama kare hatası (rmse) nasıl yorumlanır?

Regresyon analizi, bir veya daha fazla yordayıcı değişken ile bir yanıt değişkeni arasındaki ilişkiyi anlamak için kullanabileceğimiz bir tekniktir.

Bir regresyon modelinin bir veri kümesine ne kadar iyi uyduğunu değerlendirmenin bir yolu, bize modelin tahmin edilen değerleri ile veri kümesinin gerçek değerleri arasındaki ortalama mesafeyi söyleyen bir ölçüm olan ortalama karesel hatayı hesaplamaktır.

RMSE ne kadar düşük olursa, belirli bir model bir veri setine o kadar iyi “sığabilir”.

Genellikle RMSE olarak kısaltılan ortalama kare hatasını bulma formülü şöyledir:

RMSE = √ Σ(P _ben – Ö _ben ) ² / n

Altın:

• Σ “toplam” anlamına gelen süslü bir semboldür
• P _i , veri kümesindeki ^i’inci gözlem için tahmin edilen değerdir
• _Oi veri kümesindeki ^i’inci gözlem için gözlemlenen değerdir
• n örneklem büyüklüğüdür

Aşağıdaki örnek, belirli bir regresyon modeli için RMSE’nin nasıl yorumlanacağını gösterir.

Örnek: Bir regresyon modeli için RMSE nasıl yorumlanır?

Belirli bir üniversiteye giriş sınavında öğrencilerin “sınav notunu” tahmin etmek için “çalışılan saatleri” kullanan bir regresyon modeli oluşturmak istediğimizi varsayalım.

15 öğrenci için aşağıdaki verileri topluyoruz:

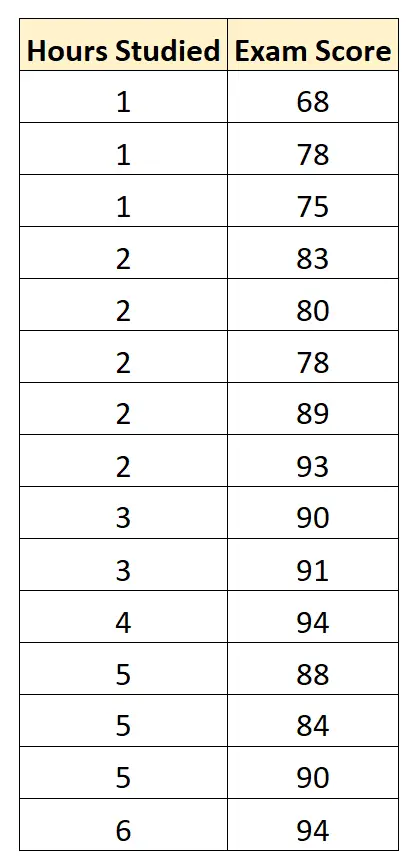
Daha sonra istatistiksel yazılımları (Excel, SPSS, R, Python gibi) kullanırız. Aşağıdaki uygun regresyon modelini bulmak için:

Sınav puanı = 75,95 + 3,08* (çalışılan saat)

Daha sonra bu denklemi, çalıştıkları saat sayısına göre her öğrencinin sınav puanını tahmin etmek için kullanabiliriz:

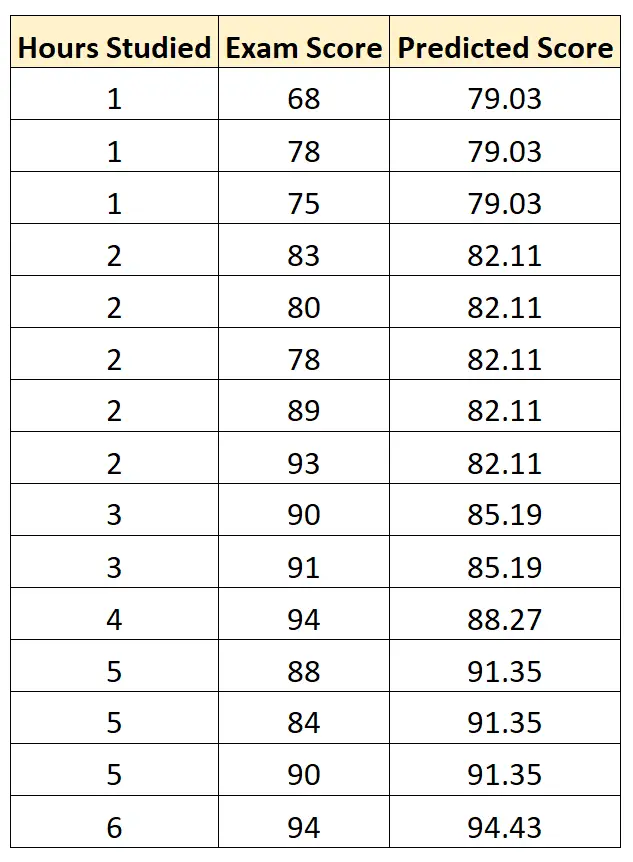
Daha sonra her tahmin edilen sınav puanı ile gerçek sınav puanı arasındaki kare farkı hesaplayabiliriz. Daha sonra bu farkların ortalamasının karekökünü alabiliriz:

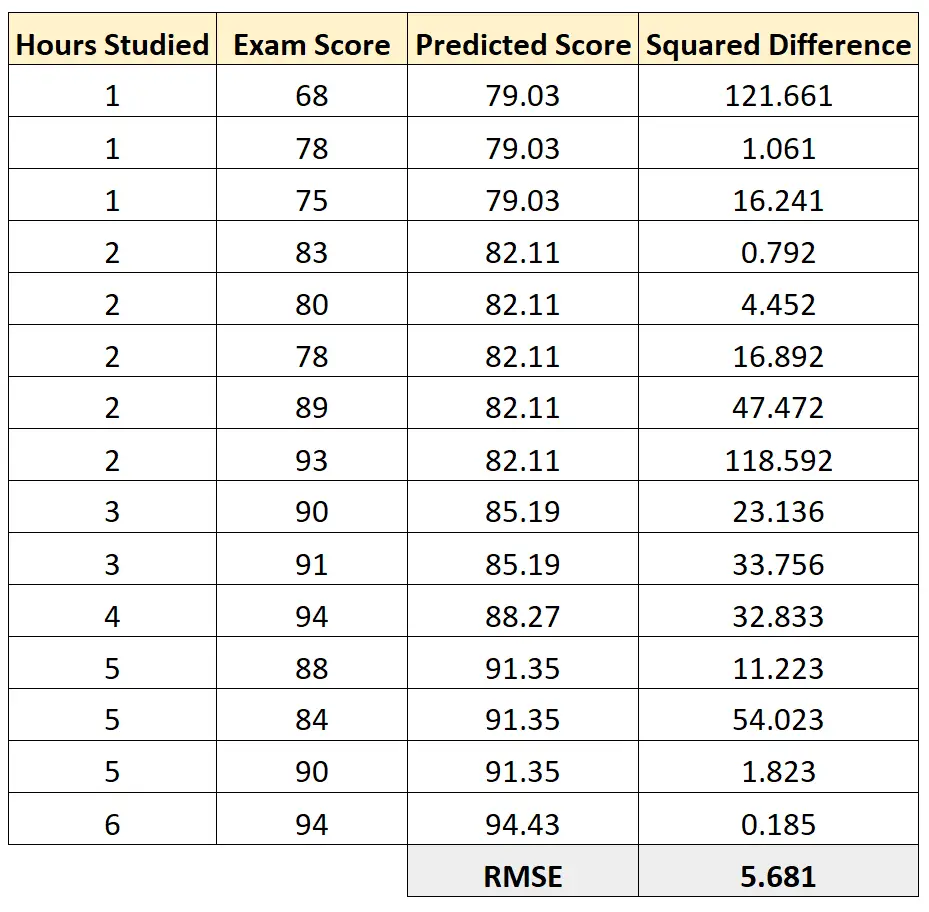
Bu regresyon modelinin RMSE’si 5,681 olarak çıkıyor.

Bir regresyon modelinin artıklarının , gözlemlenen veri değerleri ile modelin tahmin edilen değerleri arasındaki farklar olduğunu hatırlayın.

Artık = (P _i – O _i )

Altın

• P _i , veri kümesindeki ^i’inci gözlem için tahmin edilen değerdir
• _Oi veri kümesindeki ^i’inci gözlem için gözlemlenen değerdir

Bir regresyon modelinin RMSE’sinin şu şekilde hesaplandığını unutmayın:

RMSE = √ Σ(P _ben – Ö _ben ) ² / n

Bu , RMSE’nin artıkların varyansının karekökünü temsil ettiği anlamına gelir.

Bu bilinmesi gereken faydalı bir değerdir çünkü bize gözlemlenen veri değerleri ile tahmin edilen veri değerleri arasındaki ortalama mesafe hakkında fikir verir.

Bu, bize yanıt değişkenindeki varyansın ne kadarının modelin yordayıcı değişken(ler)i tarafından açıklanabileceğini söyleyen modelin R-kare değeriyle çelişir.

Farklı modellerin RMSE değerlerinin karşılaştırılması

RMSE özellikle farklı regresyon modellerinin uyumunu karşılaştırmak için kullanışlıdır.

Örneğin, öğrencilerin sınav puanlarını tahmin etmek için bir regresyon modeli oluşturmak istediğimizi ve çeşitli potansiyel modeller arasından mümkün olan en iyi modeli bulmak istediğimizi varsayalım.

Üç farklı regresyon modelini uyduğumuzu ve bunlara karşılık gelen RMSE değerlerini bulduğumuzu varsayalım:

• Model 1’in RMSE’si: 14,5
• Model 2’nin RMSE’si: 16,7
• Model 3’ün RMSE’si: 9,8

Model 3 en düşük RMSE’ye sahiptir, bu da bize üç potansiyel model arasında veri setine en iyi şekilde uyum sağlayabildiğini gösterir.

Ek kaynaklar

RMSE Hesaplayıcı
Excel’de RMSE Nasıl Hesaplanır?
R’de RMSE nasıl hesaplanır
Python’da RMSE Nasıl Hesaplanır?