R'de havuzlanmış varyans nasıl hesaplanır

İstatistiklerde küme varyansı , iki veya daha fazla küme varyansının ortalamasını ifade eder.

Gruplar arasındaki ortak varyans için tek bir sayı elde etmek amacıyla iki veya daha fazla grup varyansını “bir araya getirdiğimizi” belirtmek için “havuzlanmış” kelimesini kullanırız.

Uygulamada, havuzlanmış varyans en çok iki örneklemli t testinde kullanılır; bu test, iki popülasyonun ortalamalarının eşit olup olmadığını belirlemek için kullanılır.

İki örnek arasındaki havuzlanmış varyans genellikle _sp ² ile gösterilir ve aşağıdaki şekilde hesaplanır:

s _p ² = ( (n ₁ -1)s ₁ ² + (n ₂ -1)s ₂ ² ) / (n ₁ +n ₂ -2)

Ne yazık ki, R’de iki grup arasındaki havuzlanmış varyansı hesaplayacak yerleşik bir işlev yoktur, ancak bunu oldukça kolay hesaplayabiliriz.

Örneğin, aşağıdaki iki grup arasındaki birleştirilmiş varyansı hesaplamak istediğimizi varsayalım:

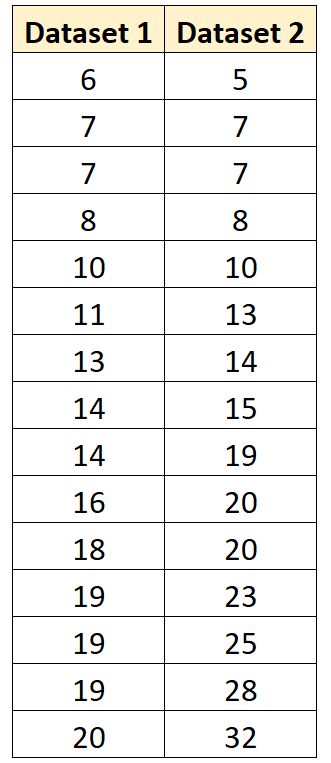
Aşağıdaki kod, R’de bu gruplar arasındaki havuzlanmış varyansın nasıl hesaplanacağını gösterir:

 #define groups of data
x1 <- c(6, 7, 7, 8, 10, 11, 13, 14, 14, 16, 18, 19, 19, 19, 20)
x2 <- c(5, 7, 7, 8, 10, 13, 14, 15, 19, 20, 20, 23, 25, 28, 32)

#calculate sample size of each group
n1 <- length(x1)
n2 <- length(x2)

#calculate sample variance of each group
var1 <- var(x1)
var2 <- var(x2)

#calculate pooled variance between the two groups
pooled <- ((n1-1)*var1 + (n2-1)*var2) / (n1+n2-2)

#display pooled variance
pooled

[1] 46.97143

Bu iki grup arasındaki toplu varyans 46,97143 olarak ortaya çıkıyor.

Ek kaynaklar

Kümelenmiş varyans nedir? (Tanım ve örnek)
Paketlenmiş Boşluk Hesaplayıcı
Excel’de Havuzlanmış Varyans Nasıl Hesaplanır