Python'da roc eğrisi nasıl çizilir (adım adım)

Lojistik regresyon, yanıt değişkeni ikili olduğunda bir regresyon modeline uymak için kullandığımız istatistiksel bir yöntemdir. Lojistik regresyon modelinin bir veri kümesine ne kadar iyi uyduğunu değerlendirmek için aşağıdaki iki ölçüme bakabiliriz:

• Duyarlılık: Sonuç gerçekten olumluyken modelin bir gözlem için olumlu bir sonuç tahmin etme olasılığı. Buna aynı zamanda “gerçek pozitif oran” da denir.
• Özgüllük: Sonuç gerçekten negatif olduğunda modelin bir gözlem için negatif bir sonuç öngörme olasılığı. Buna aynı zamanda “gerçek negatif oran” da denir.

Bu iki ölçümü görselleştirmenin bir yolu, “alıcı çalışma karakteristiği” eğrisi anlamına gelen bir ROC eğrisi oluşturmaktır. Bu, lojistik regresyon modelinin duyarlılığını ve özgüllüğünü gösteren bir grafiktir.

Aşağıdaki adım adım örnek, Python’da bir ROC eğrisinin nasıl oluşturulacağını ve yorumlanacağını gösterir.

Adım 1: Gerekli paketleri içe aktarın

Öncelikle Python’da lojistik regresyon gerçekleştirmek için gerekli paketleri içe aktaracağız:

 import pandas as pd
import numpy as np
from sklearn. model_selection import train_test_split
from sklearn. linear_model import LogisticRegression
from sklearn import metrics
import matplotlib. pyplot as plt

Adım 2: Lojistik regresyon modelini yerleştirin

Daha sonra, bir veri kümesini içe aktaracağız ve buna bir lojistik regresyon modeli yerleştireceğiz:

 #import dataset from CSV file on Github
url = "https://raw.githubusercontent.com/Statorials/Python-Guides/main/default.csv"
data = pd. read_csv (url)

#define the predictor variables and the response variable
X = data[[' student ',' balance ',' income ']]
y = data[' default ']

#split the dataset into training (70%) and testing (30%) sets
X_train,X_test,y_train,y_test = train_test_split(X,y,test_size=0.3,random_state=0) 

#instantiate the model
log_regression = LogisticRegression()

#fit the model using the training data
log_regression. fit (X_train,y_train)

Adım 3: ROC eğrisini çizin

Daha sonra, gerçek pozitif oranı ve yanlış pozitif oranı hesaplayacağız ve Matplotlib veri görselleştirme paketini kullanarak bir ROC eğrisi oluşturacağız:

 #define metrics
y_pred_proba = log_regression. predict_proba (X_test)[::,1]
fpr, tpr, _ = metrics. roc_curve (y_test, y_pred_proba)

#create ROC curve
plt. plot (fpr,tpr)
plt. ylabel (' True Positive Rate ')
plt. xlabel (' False Positive Rate ')
plt. show () 

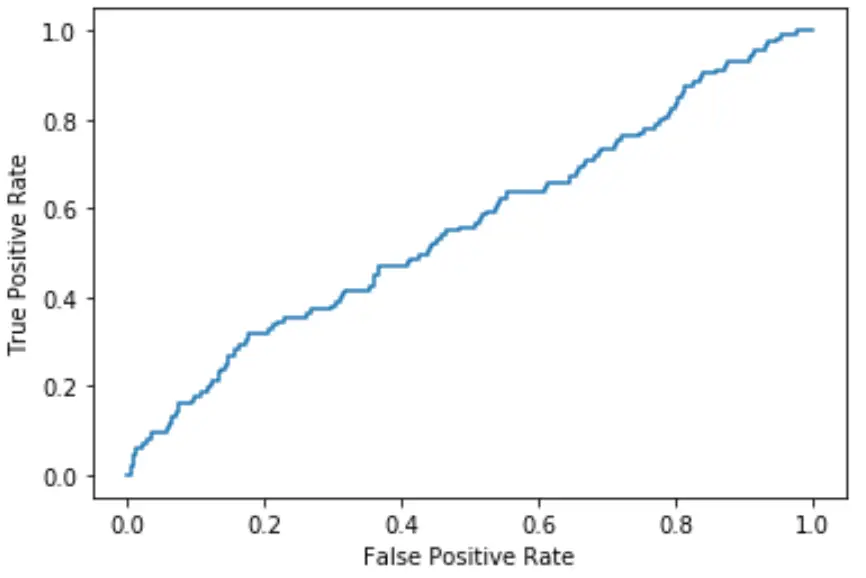
Eğri grafiğin sol üst köşesine ne kadar yakın olursa, model verileri kategorilere göre o kadar iyi sınıflandırabilir.

Yukarıdaki grafikten görebileceğimiz gibi, bu lojistik regresyon modeli, verileri kategorilere ayırma konusunda oldukça zayıf bir iş çıkarıyor.

Bunu ölçmek için, bize grafiğin ne kadarının eğrinin altında olduğunu söyleyen AUC’yi (eğrinin altındaki alanı) hesaplayabiliriz.

AUC 1’e ne kadar yakınsa model o kadar iyidir. AUC değeri 0,5’e eşit olan bir model, rastgele sınıflandırma yapan bir modelden daha iyi değildir.

Adım 4: AUC’yi hesaplayın

Modelin AUC’sini hesaplamak ve bunu ROC grafiğinin sağ alt köşesinde görüntülemek için aşağıdaki kodu kullanabiliriz:

 #define metrics
y_pred_proba = log_regression. predict_proba (X_test)[::,1]
fpr, tpr, _ = metrics. roc_curve (y_test, y_pred_proba)
auc = metrics. roc_auc_score (y_test, y_pred_proba)

#create ROC curve
plt. plot (fpr,tpr,label=" AUC= "+str(auc))
plt. ylabel (' True Positive Rate ')
plt. xlabel (' False Positive Rate ')
plt. legend (loc=4)
plt. show () 

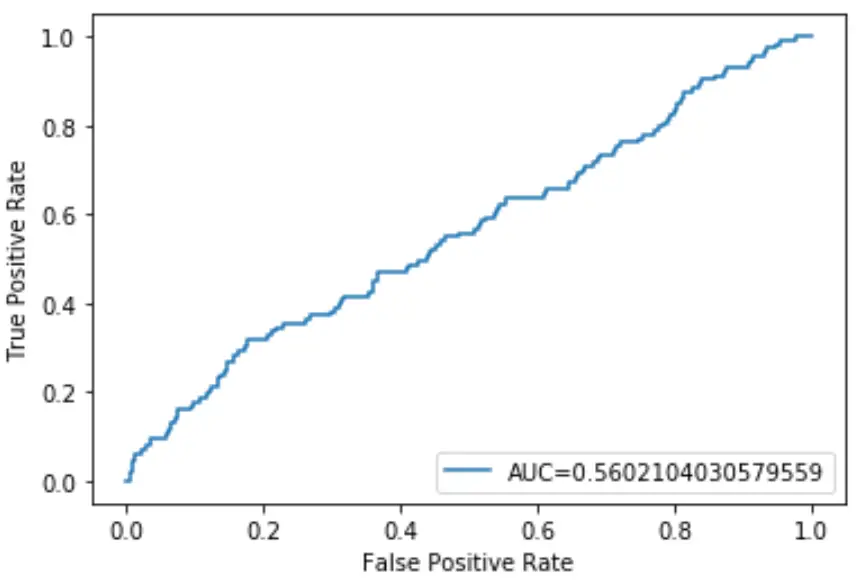
Bu lojistik regresyon modelinin AUC’si 0,5602 olarak çıkıyor. Bu rakamın 0,5’e yakın olması, modelin verileri sınıflandırma konusunda kötü bir iş çıkardığını doğruluyor.

İlgili: Python’da Çoklu ROC Eğrileri Nasıl Çizilir