Sabit varyans hipotezi: tanım ve örnek
Doğrusal regresyon, bir veya daha fazla öngörücü değişken ile bir yanıt değişkeni arasındaki ilişkiyi ölçmek için kullandığımız bir tekniktir.
Doğrusal regresyonun temel varsayımlarından biri, artıkların, yordayıcı değişken(ler)in her seviyesinde sabit varyansa sahip olmasıdır.
Eğer bu varsayım doğrulanmazsa, artıklar değişen varyans sorunu yaşayacaktır. Bu durumda model katsayı tahminleri güvenilmez hale gelir.
Sabit varyans nasıl değerlendirilir?
Bir regresyon modelinin artıklarının sabit varyansa sahip olup olmadığını belirlemenin en yaygın yolu, artıklara karşı uygun değerlerin bir grafiğini oluşturmaktır.
Bu, regresyon modelinin x ekseni boyunca uydurulmuş değerlerini ve y ekseni boyunca uydurulmuş bu değerlerin artıklarını görüntüleyen bir çizim türüdür.
Artıkların dağılımı, uydurulan değerlerin her seviyesinde yaklaşık olarak eşitse, sabit varyans varsayımının karşılandığını söyleriz.
Aksi takdirde, artıkların dağılımı sistematik olarak artar veya azalırsa, bu varsayımın ihlal edilmesi muhtemeldir.
Not : Bu tür bir grafik yalnızca veri kümesine bir regresyon modeli yerleştirildikten sonra oluşturulabilir.
Aşağıdaki grafik, sabit varyansı gösteren artıklara karşı uygun değerlerin grafiğinin bir örneğini göstermektedir:
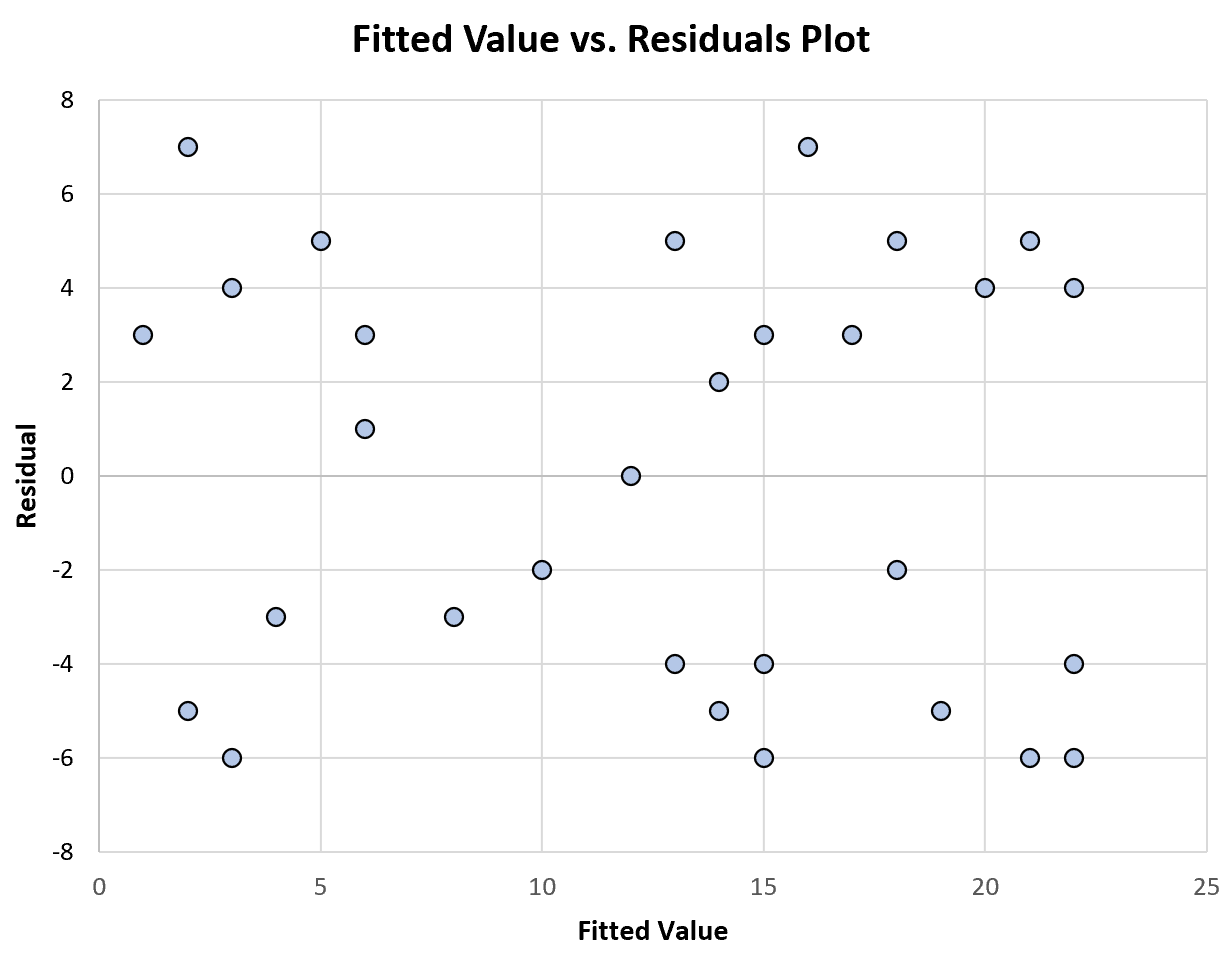
Artıkların, uydurulan değerlerin her seviyesinde yaklaşık olarak sabit bir varyansla, belirli bir düzende, sıfır çevresinde nasıl rastgele dağıldığına dikkat edin.
Aşağıdaki grafik, sabit olmayan varyans gösteren artıklara karşı uygun değerlerin grafiğinin bir örneğini göstermektedir:
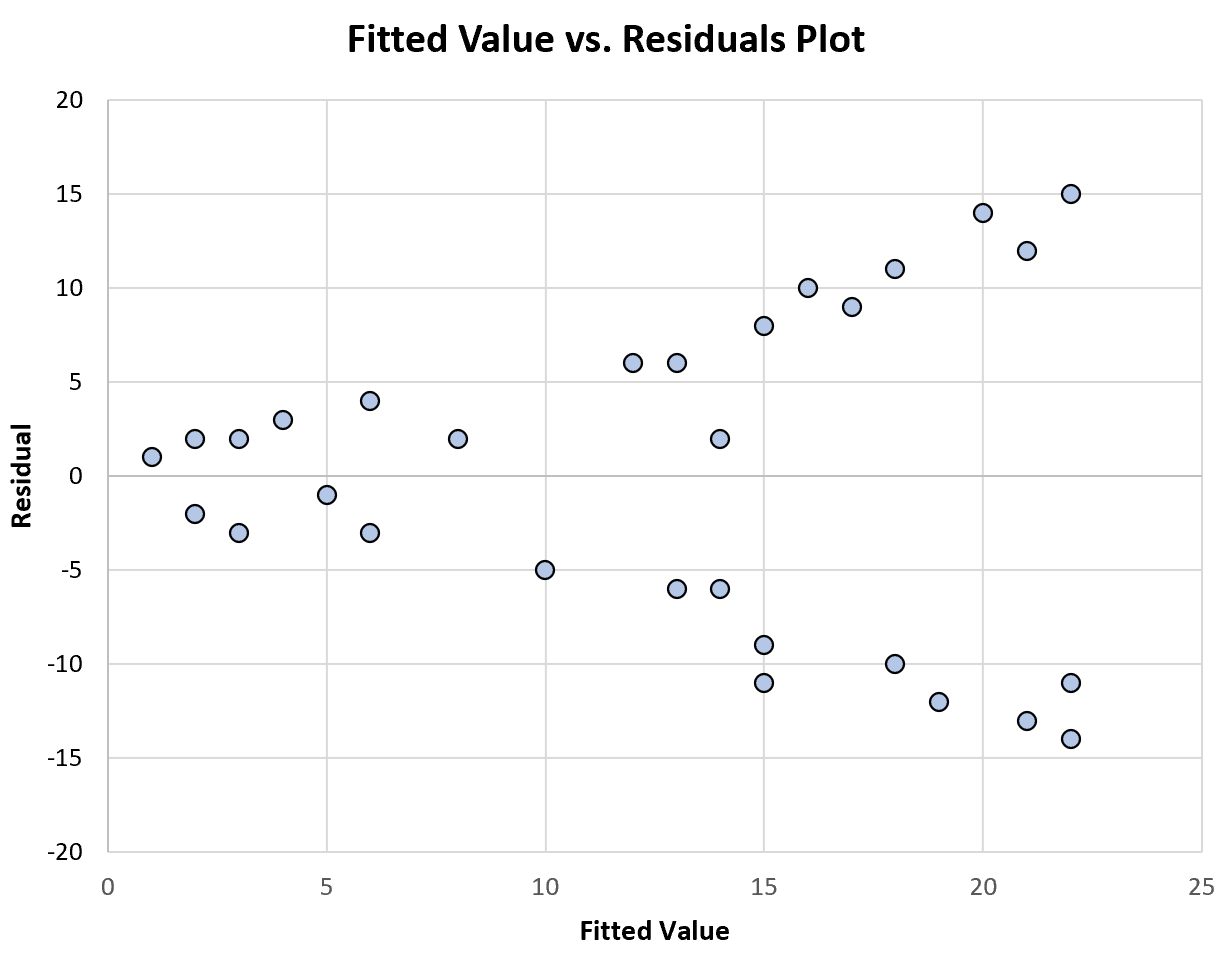
Takılan değerler arttıkça artıkların dağılımının da büyüdüğünü unutmayın. Bu, sabit olmayan varyansın tipik bir işaretidir.
Bu bize, regresyon modelimizin artıklarda sabit olmayan varyanstan muzdarip olduğunu ve bu nedenle model katsayı tahminlerinin güvenilmez olduğunu söyler.
Sabit sapma ihlali nasıl düzeltilir?
Sabit varyans varsayımı ihlal edilirse, bu sorunu çözmenin en yaygın yolu, yanıt değişkenini üç dönüşümden birini kullanarak dönüştürmektir:
1. Günlük Dönüşümü: Yanıt değişkenini y’den log(y)’ ye dönüştürün
2. Karekök dönüşümü: yanıt değişkenini y’den √y’ye dönüştürün
3. Küp kök dönüşümü: yanıt değişkenini y’den y 1/3’e dönüştürün
Bu dönüşümlerin gerçekleştirilmesiyle sabit olmayan varyans sorunu genel olarak ortadan kalkar.
Ek kaynaklar
Aşağıdaki eğitimler doğrusal regresyon ve artık analiz hakkında ek bilgi sağlar:
Basit Doğrusal Regresyona Giriş
Çoklu Doğrusal Regresyona Giriş
Doğrusal regresyonun dört varsayımı
İstatistiklerde artıklar nelerdir?