Sas'ta güven aralıkları nasıl hesaplanır?

Güven aralığı, belirli bir güven düzeyine sahip bir popülasyon parametresini içermesi muhtemel bir değer aralığıdır.

Bu eğitimde R’de aşağıdaki güven aralıklarının nasıl hesaplanacağı açıklanmaktadır:

1. Popülasyon ortalaması için güven aralığı

2. Popülasyon ortalamalarındaki fark için güven aralığı

Hadi gidelim!

Örnek 1: SAS’ta popülasyon ortalaması için güven aralığı

Hepsi aynı türe ait olan 12 bitkiden oluşan rastgele bir örneğin yüksekliğini (inç cinsinden) içeren aşağıdaki veri setine sahip olduğumuzu varsayalım:

 /*create dataset*/
data my_data;
    inputHeight ;
    datalines ;
14
14
16
13
12
17
15
14
15
13
15
14
;
run ;

/*view dataset*/
proc print data =my_data; 

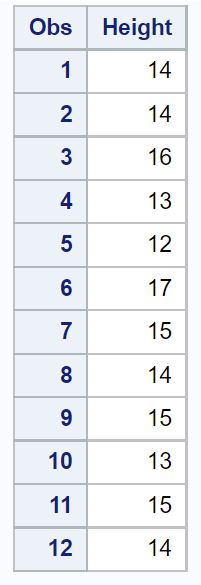
Bu türün gerçek ortalama popülasyon büyüklüğü için %95’lik bir güven düzeyi hesaplamak istediğimizi varsayalım.

Bunu yapmak için SAS’ta aşağıdaki kodu kullanabiliriz:

 /*generate 95% confidence interval for population mean*/
proc ttest data =my_data alpha = 0.05 ;
    varHeight ;
run ;

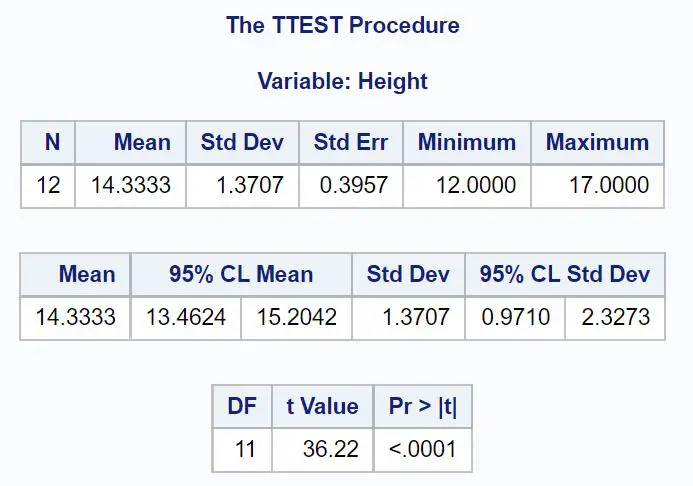
Ortalama değeri örnek ortalamasını belirtir ve %95 CL Ortalamasından küçük değerler popülasyon ortalaması için %95 güven aralığını gösterir.

Sonuçlardan, bu popülasyonun ortalama bitki ağırlığı için %95 güven aralığının [13,4624 inç, 15,2042 inç] olduğunu görebiliriz.

Örnek 2: SAS’ta popülasyon ortalamalarındaki farka ilişkin güven aralığı

İki farklı türe ait rastgele bir bitki örneğinin yüksekliğini (inç cinsinden) içeren aşağıdaki veri setine sahip olduğumuzu varsayalım:

 /*create dataset*/
data my_data2;
    input Species $Height;
    datalines ;
At 14
At 14
At 16
At 13
AT 12
At 17
At 15
At 14
At 15
At 13
B15
B14
B 19
B 19
B17
B 18
B20
B 19
B17
B15
;
run ;

/*view dataset*/
proc print data =my_data2; 

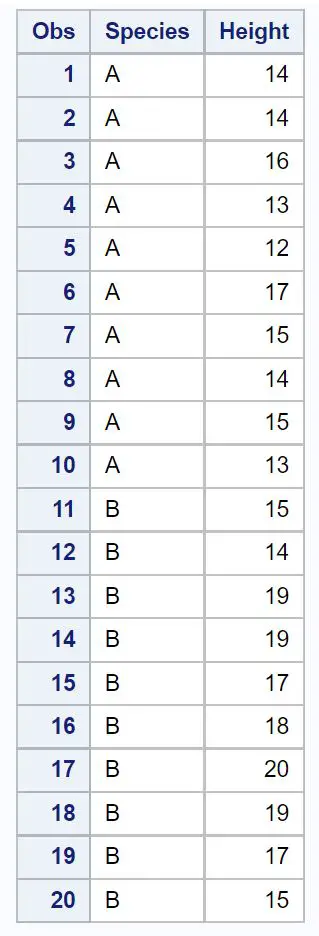
A türü ile B türü arasındaki ortalama popülasyon büyüklüğü farkı için %95’lik bir güven düzeyi hesaplamak istediğimizi varsayalım.

Bunu yapmak için SAS’ta aşağıdaki kodu kullanabiliriz:

 /*sort data by Species to ensure confidence interval is calculated correctly*/
proc sort data =my_data2;
    by Species;
run ;

/*generate 95% confidence interval for difference in population means*/
proc ttest data =my_data2 alpha = 0.05 ;
    class Species;
    varHeight ;
run ;

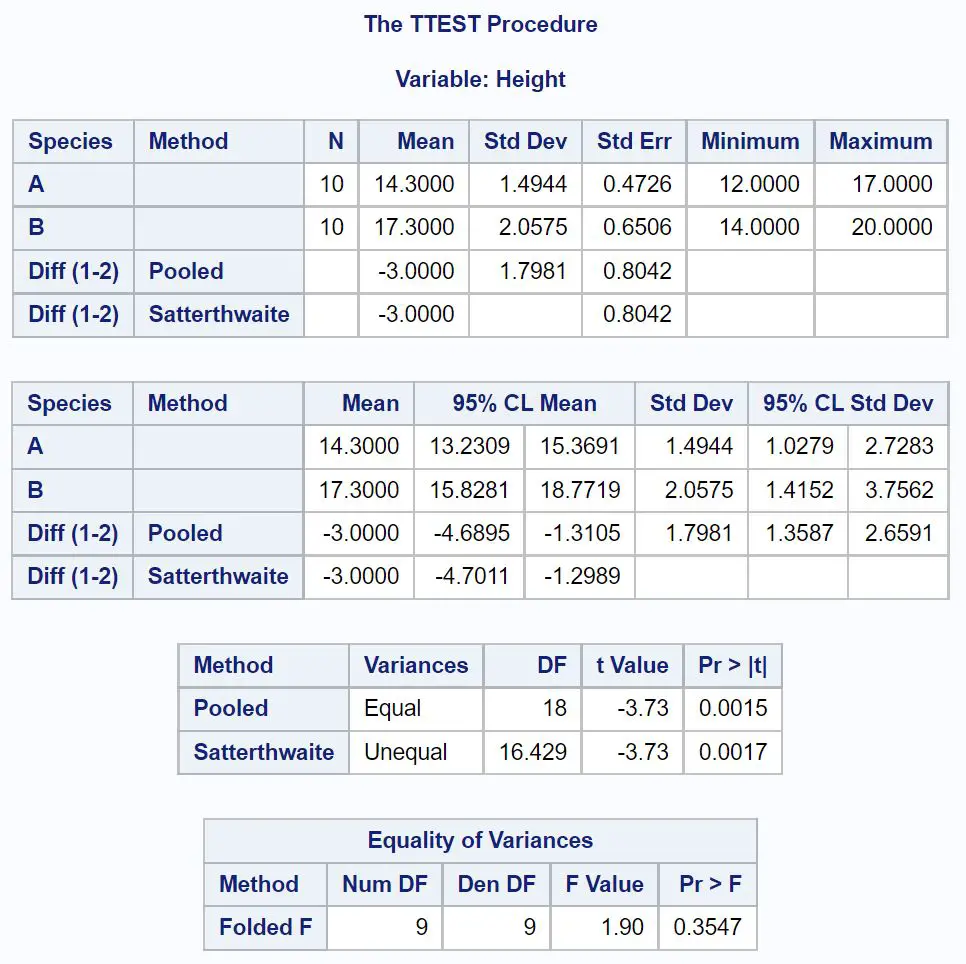
Sonuçta bakmamız gereken ilk tablo, her bir örnek arasındaki varyansın eşit olup olmadığını test eden Varyansların Eşitliği tablosudur.

Bu tabloda p değeri 0,05’ten küçük olmadığından iki grup arasındaki farkların eşit olduğunu varsayabiliriz.

Böylece popülasyon ortalamalarındaki fark için %95 güven aralığını bulmak üzere birleştirilmiş varyansı kullanan doğruya bakabiliriz.

Sonuçtan, popülasyon ortalamaları arasındaki fark için %95 güven aralığının [-4,6895 inç, -1,1305 inç] olduğunu görebiliriz.

Bu bize A türünün ve B türünün ortalama bitki boyu arasındaki gerçek farkın -4,6895 inç ile -1,1305 inç arasında olduğundan %95 emin olabileceğimizi söylüyor.

0’ın bu güven aralığında olmaması , iki popülasyonun ortalamaları arasında istatistiksel olarak anlamlı bir fark olduğunu gösterir.

Ek kaynaklar

Aşağıdaki eğitimlerde SAS’ta diğer ortak görevlerin nasıl gerçekleştirileceği açıklanmaktadır:

SAS’ta tek örnekli t testi nasıl yapılır?
SAS’ta iki örnekli t testi nasıl yapılır?
SAS’ta eşleştirilmiş örnekler t testi nasıl gerçekleştirilir?