Sas'ta aic nasıl hesaplanır (örnekle)

Akaike Bilgi Kriteri (AIC), çoklu regresyon modellerinin uyumunu karşılaştırmak için kullanılan bir ölçümdür.

Aşağıdaki şekilde hesaplanır:

AIC = 2K – 2 ln (L)

Altın:

• K: Model parametrelerinin sayısı. K’nin varsayılan değeri 2’dir, dolayısıyla yalnızca bir tahmin değişkeni olan bir modelin K değeri 2+1 = 3 olacaktır.
• ln (L) : Modelin log-olasılığı. Çoğu istatistik yazılımı bu değeri sizin için otomatik olarak hesaplayabilir.

AIC, verilerdeki en fazla varyasyonu açıklayan modeli bulmak ve aşırı sayıda parametre kullanan modelleri cezalandırmak için tasarlanmıştır.

Birden fazla regresyon modelini yerleştirdikten sonra her modelin AIC değerini karşılaştırabilirsiniz. AIC ne kadar düşükse model o kadar uygundur.

Aşağıdaki örnek, SAS’taki farklı regresyon modelleri için AIC’nin nasıl hesaplanacağını gösterir.

Örnek: SAS’ta AIC nasıl hesaplanır?

Öğrencilerin bir sınıfta alacağı sınav notunu tahmin etmek için üç farklı çoklu doğrusal regresyon modelini eşleştirmek istediğimizi varsayalım.

Her modelde kullanacağımız tahmin değişkenleri şunlardır:

• Model 1’deki yordayıcı değişkenler: ders çalışmak için harcanan saatler
• Model 2’deki yordayıcı değişkenler: geçmiş uygulamalı sınavlar
• Model 3’teki yordayıcı değişkenler: ders çalışmak için harcanan saatler ve alınan pratik sınavlar

Öncelikle 20 öğrenciye yönelik bu bilgileri içeren bir veri seti oluşturmak için aşağıdaki kodu kullanacağız:

 /*create dataset*/
data exam_data;
    input hours prep_exams score;
    datalines ;
1 1 76
2 3 78
2 3 85
4 5 88
2 2 72
1 2 69
5 1 94
4 1 94
2 0 88
4 3 92
4 4 90
3 3 75
6 2 96
5 4 90
3 4 82
4 4 85
6 5 99
2 1 83
1 0 62
2 1 76
;
run ;

Daha sonra, bu regresyon modellerinin her birine uyacak şekilde proc reg kullanacağız ve her model için AIC değerlerini hesaplamak amacıylaselection =adjrsq sse aic ifadesini kullanacağız:

 /*fit multiple linear regression models and calculate AIC for each model*/
proc reg data =exam_data;
    model score = hours prep_exams / selection=adjrsq sse aic;
run ; 

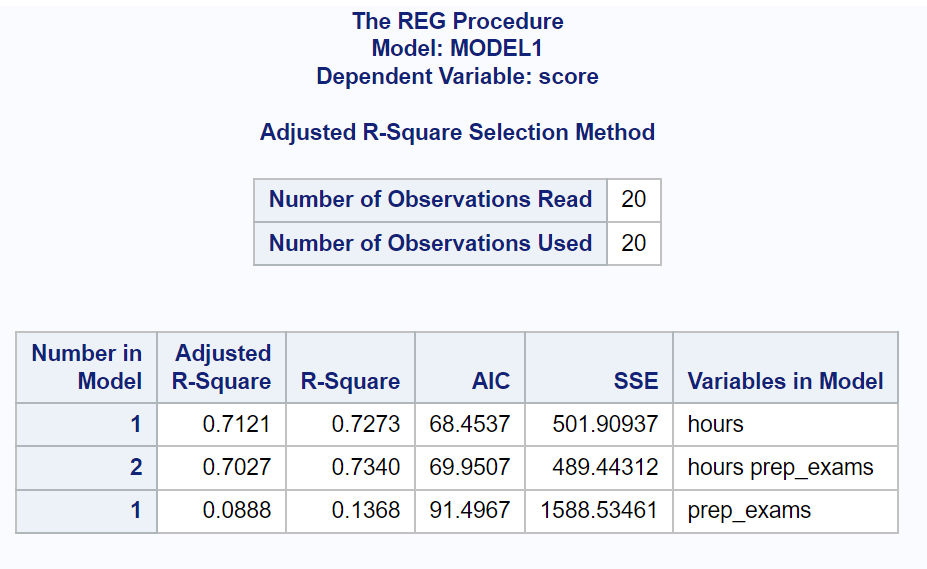
Sonuçtan her model için AIC değerlerini görebiliriz:

• Tahmin değişkeni olarak saatlerle birlikte AIC: 68.4537
• Tahmin değişkenleri olarak saat ve sınavları içeren AIC: 69,9507
• Tahmin değişkeni olarak sınavlarla AIC: 91.4967

En düşük AIC değerine sahip model, yordayıcı değişken olarak yalnızca saatleri içeren modeldir.

Bu nedenle aşağıdaki modelin verilere en iyi şekilde uyduğunu beyan ederiz:

Puan = β ₀ + β ₁ (çalışılan saat)

Bu modeli en iyisi olarak belirledikten sonra, onu yerleştirebilir ve çalışılan saat ile öğrenci notu arasındaki kesin ilişkiyi belirlemek için R-kare değeri ve beta katsayıları da dahil olmak üzere sonuçları analiz edebiliriz. ‘Final Sınavı.

Ek kaynaklar

Aşağıdaki eğitimlerde SAS’ta diğer ortak görevlerin nasıl gerçekleştirileceği açıklanmaktadır:

SAS’ta basit doğrusal regresyon nasıl gerçekleştirilir?
SAS’ta çoklu doğrusal regresyon nasıl gerçekleştirilir?
SAS’ta R-kare nasıl hesaplanır
SAS’ta RMSE nasıl hesaplanır