Sas'ta basit doğrusal regresyon nasıl gerçekleştirilir?

Basit doğrusal regresyon, yordayıcı değişken ile yanıt değişkeni arasındaki ilişkiyi anlamak için kullanabileceğimiz bir tekniktir.

Bu teknik, verilere en iyi “uyan” çizgiyi bulur ve aşağıdaki formu alır:

ŷ = b ₀ + b ₁ x

Altın:

• ŷ : Tahmini yanıt değeri
• b ₀ : Regresyon çizgisinin başlangıcı
• b ₁ : Regresyon çizgisinin eğimi

Bu denklem, yordayıcı değişken ile yanıt değişkeni arasındaki ilişkiyi anlamamıza yardımcı olur.

Aşağıdaki adım adım örnek, SAS’ta basit bir doğrusal regresyonun nasıl gerçekleştirileceğini gösterir.

1. Adım: Verileri oluşturun

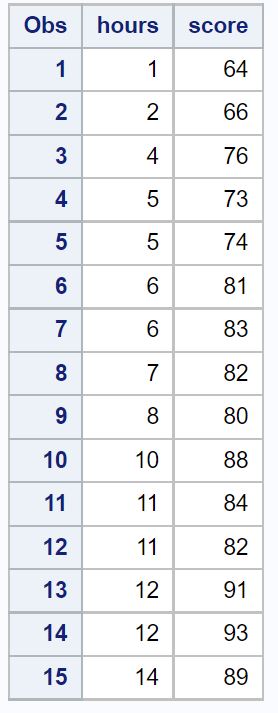
Bu örnekte 15 öğrencinin toplam ders saatini ve final sınav notunu içeren bir veri seti oluşturacağız.

Tahmin edici değişken olarak saatleri ve yanıt değişkeni olarak puanı kullanarak basit bir doğrusal regresyon modeli uygulayacağız.

Aşağıdaki kod, bu veri kümesinin SAS’ta nasıl oluşturulacağını gösterir:

 /*create dataset*/
data exam_data;
    input hours score;
    datalines ;
1 64
2 66
4 76
5 73
5 74
6 81
6 83
7 82
8 80
10 88
11 84
11 82
12 91
12 93
14 89
;
run ;

/*view dataset*/
proc print data =exam_data;

Adım 2: Basit doğrusal regresyon modelini yerleştirin

Daha sonra basit doğrusal regresyon modeline uyum sağlamak için proc reg’i kullanacağız:

 /*fit simple linear regression model*/
proc reg data =exam_data;
   model score = hours;
run ; 

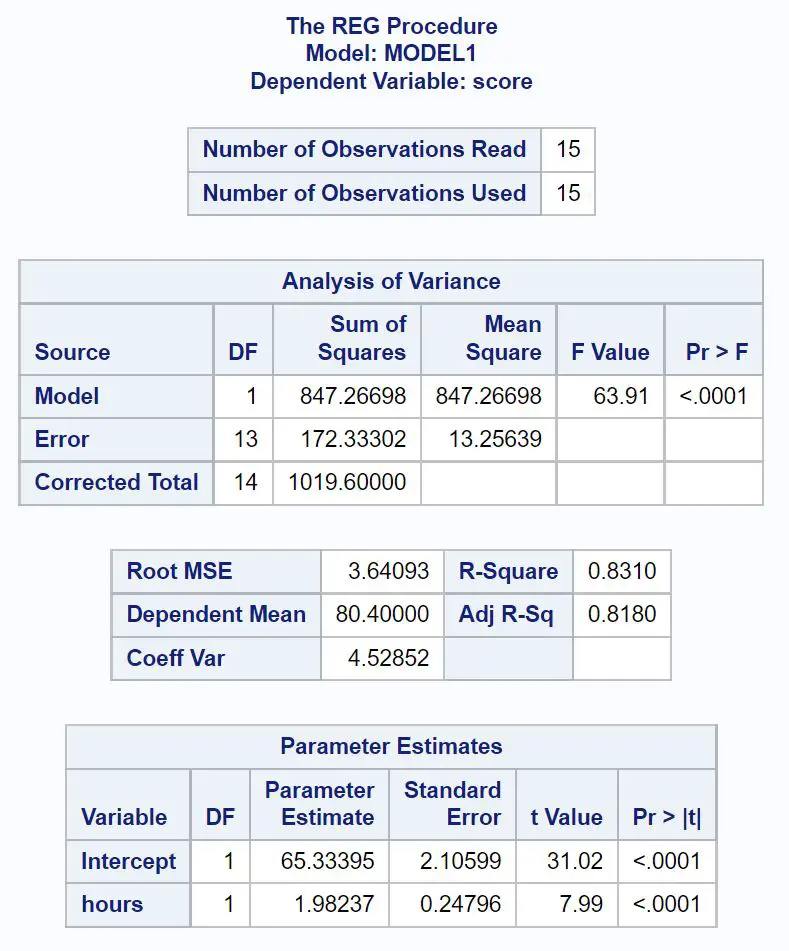
Sonuçtaki her tablodaki en önemli değerleri şu şekilde yorumlayabilirsiniz:

Boşluk analizi tablosu:

Regresyon modelinin genel F değeri 63,91’dir ve karşılık gelen p değeri <0,0001’dir .

Bu p değeri 0,05’ten küçük olduğundan regresyon modelinin bir bütün olarak istatistiksel olarak anlamlı olduğu sonucuna varıyoruz. Başka bir deyişle saatler, sınav sonuçlarını tahmin etmede faydalı bir değişkendir.

Model uyum tablosu:

R-Kare değeri bize, çalışılan saat sayısıyla açıklanabilecek sınav puanlarındaki değişimin yüzdesini verir.

Genel olarak, bir regresyon modelinin R-kare değeri ne kadar büyük olursa, yordayıcı değişkenlerin yanıt değişkeninin değerini tahmin etmede o kadar iyi olur.

Bu durumda sınav puanlarındaki farklılığın %83,1’i çalışılan saat sayısıyla açıklanabilir. Bu değerin oldukça yüksek olması, çalışılan saatin sınav sonuçlarını tahmin etmede oldukça faydalı bir değişken olduğunu göstermektedir.

Parametre tahminleri tablosu:

Bu tablodan uygun regresyon denklemini görebiliriz:

Puan = 65,33 + 1,98*(saat)

Bunu, çalışılan her ek saatin sınav puanında ortalama 1,98 puanlık bir artışla ilişkili olduğu şeklinde yorumluyoruz.

Orijinal değer bize sıfır saat ders çalışan bir öğrencinin ortalama sınav puanının 65,33 olduğunu söylüyor.

Bu denklemi, öğrencinin ders çalıştığı saat sayısına göre beklenen sınav puanını bulmak için de kullanabiliriz.

Örneğin 10 saat ders çalışan bir öğrencinin sınav puanının 85,13 olması gerekir:

Puan = 65,33 + 1,98*(10) = 85,13

Bu tabloda saatlere ilişkin p değeri (<0,0001) 0,05’ten küçük olduğundan, bunun istatistiksel olarak anlamlı bir yordayıcı değişken olduğu sonucuna varıyoruz.

3. Adım: Kalan grafikleri analiz edin

Basit doğrusal regresyon, model artıkları hakkında iki önemlivarsayımda bulunur:

• Artıklar normal dağılıma sahiptir.
• Artıklar, yordayıcı değişkenin her seviyesinde eşit varyansa (” eşvaryanslılık “) sahiptir.

Bu varsayımlar karşılanmazsa regresyon modelimizin sonuçları güvenilir olmayabilir.

Bu varsayımların karşılandığını doğrulamak için SAS’ın çıktıda otomatik olarak gösterdiği kalan grafikleri analiz edebiliriz:

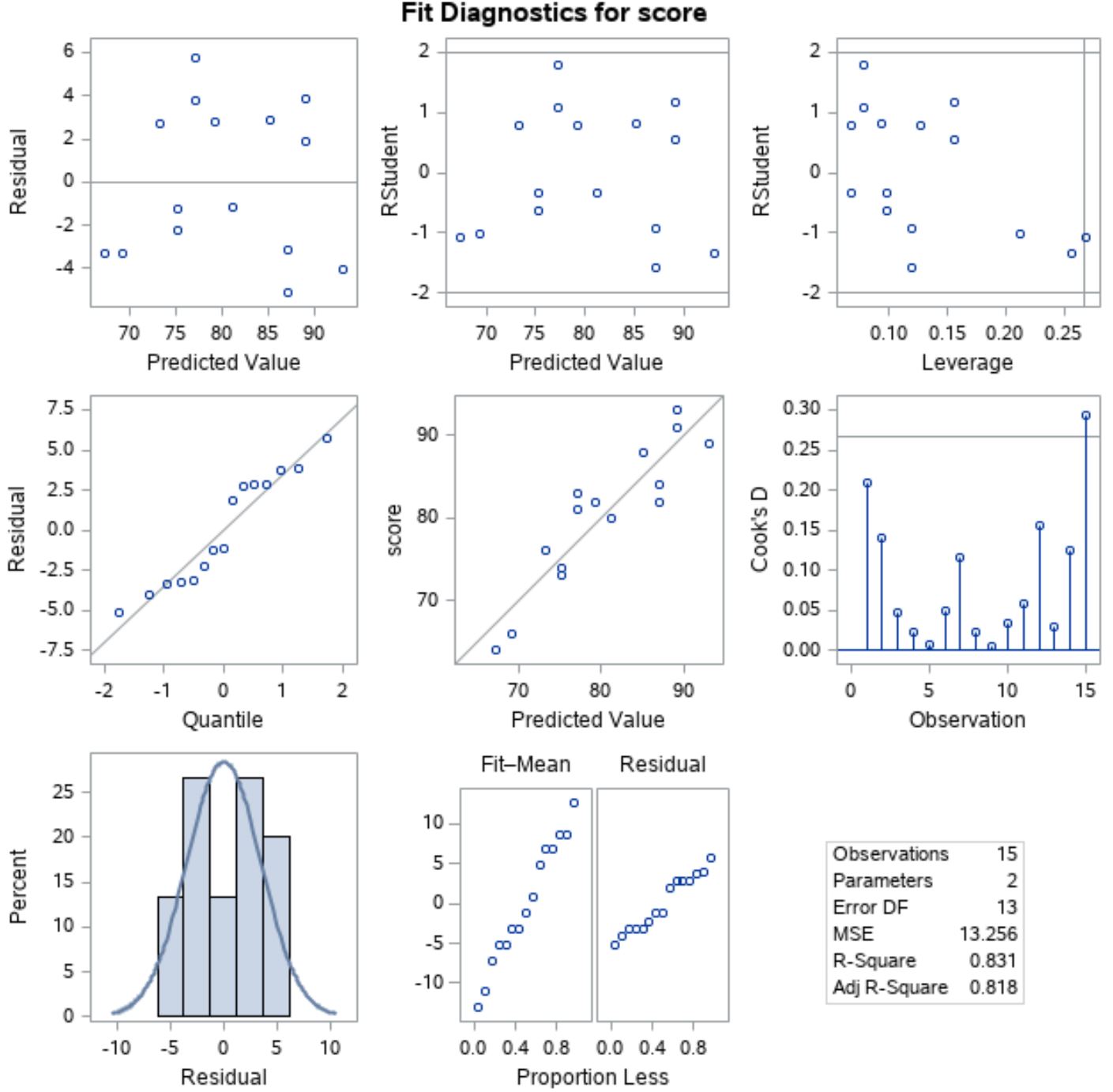
Artıkların normal şekilde dağıldığını doğrulamak için, orta çizginin sol konumundaki grafiği, x ekseni boyunca “Kantil” ve y ekseni boyunca “Artık” ile analiz edebiliriz.

Bu çizime QQ grafiği denir, “kantil-nicelik” kelimesinin kısaltmasıdır ve verilerin normal şekilde dağılıp dağılmadığını belirlemek için kullanılır. Veriler normal olarak dağılıyorsa, QQ grafiğindeki noktalar düz bir çapraz çizgi üzerinde yer alacaktır.

Grafikten noktaların kabaca düz bir çapraz çizgi boyunca uzandığını görebiliriz, dolayısıyla artıkların normal şekilde dağıldığını varsayabiliriz.

Daha sonra, artıkların homoskedastik olduğunu doğrulamak için, x ekseni boyunca “Tahmin edilen değer” ve y ekseni boyunca “Artık” ile ilk satırın sol konumundaki çizime bakabiliriz.

Eğer çizim noktaları net bir model olmadan sıfır etrafında rastgele dağılmışsa, o zaman artıkların homoskedastic olduğunu varsayabiliriz.

Grafikten, noktaların grafik boyunca her düzeyde yaklaşık olarak eşit varyansla sıfır etrafında rastgele dağıldığını görebiliriz, dolayısıyla artıkların homoskedastik olduğunu varsayabiliriz.

Her iki varsayım da karşılandığı için basit doğrusal regresyon modelinin sonuçlarının güvenilir olduğunu varsayabiliriz.

Ek kaynaklar

Aşağıdaki eğitimlerde SAS’ta diğer ortak görevlerin nasıl gerçekleştirileceği açıklanmaktadır:

SAS’ta tek yönlü ANOVA nasıl gerçekleştirilir?
SAS’ta iki yönlü ANOVA nasıl gerçekleştirilir?
SAS’ta korelasyon nasıl hesaplanır?