Sas'ta çoklu doğrusal regresyon nasıl gerçekleştirilir?

Çoklu doğrusal regresyon, iki veya daha fazla yordayıcı değişken ile bir yanıt değişkeni arasındaki ilişkiyi anlamak için kullanabileceğimiz bir yöntemdir.

Bu eğitimde SAS’ta çoklu doğrusal regresyonun nasıl gerçekleştirileceği açıklanmaktadır.

1. Adım: Verileri oluşturun

Öğrencilerin final sınavı notunu tahmin etmek için ders çalışmak için harcanan saat sayısını ve alınan uygulama sınavlarının sayısını kullanan çoklu doğrusal regresyon modelini uyarlamak istediğimizi varsayalım:

Sınav puanı = β ₀ + β ₁ (saat) + β ₂ (hazırlık sınavları)

Öncelikle 20 öğrenciye yönelik bu bilgileri içeren bir veri seti oluşturmak için aşağıdaki kodu kullanacağız:

 /*create dataset*/
data exam_data;
    input hours prep_exams score;
    datalines ;
1 1 76
2 3 78
2 3 85
4 5 88
2 2 72
1 2 69
5 1 94
4 1 94
2 0 88
4 3 92
4 4 90
3 3 75
6 2 96
5 4 90
3 4 82
4 4 85
6 5 99
2 1 83
1 0 62
2 1 76
;
run ;

Adım 2: Çoklu Doğrusal Regresyon Gerçekleştirin

Daha sonra, verilere çoklu doğrusal regresyon modeli uydurmak için proc reg’i kullanacağız:

 /*fit multiple linear regression model*/
proc reg data =exam_data;
    model score = hours prep_exams;
run ; 

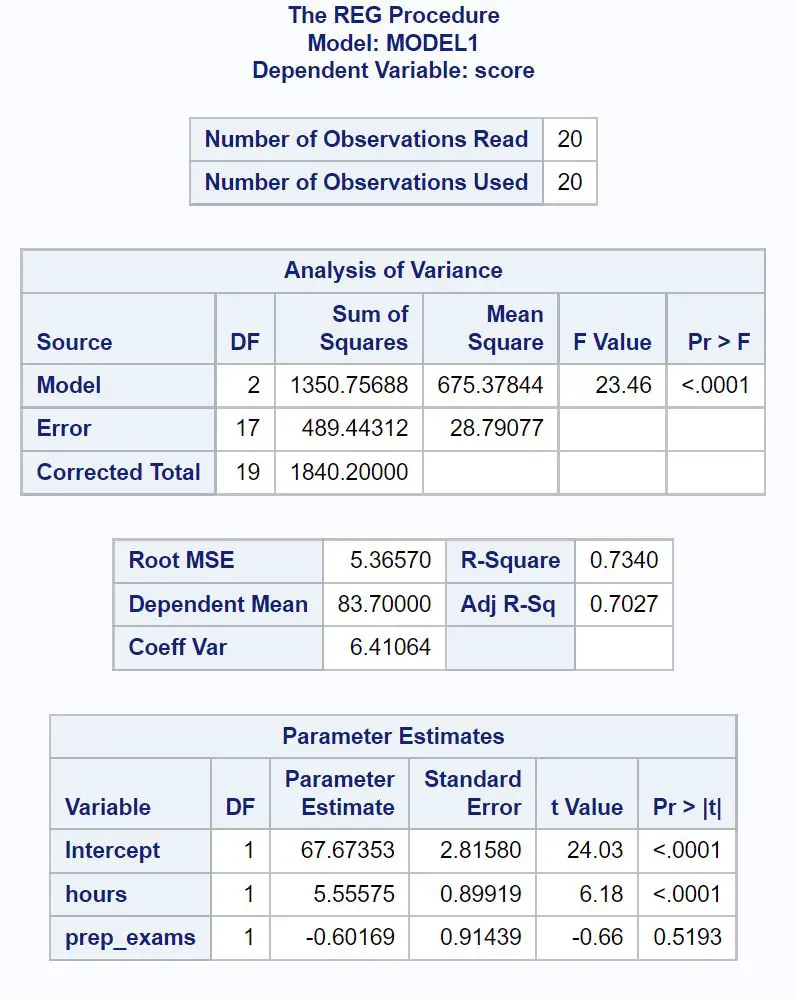
Her tablodaki en alakalı sayıları nasıl yorumlayacağınız aşağıda açıklanmıştır:

Boşluk analizi tablosu:

Regresyon modelinin genel F değeri 23,46’dır ve karşılık gelen p değeri <0,0001’dir .

Bu p değeri 0,05’ten küçük olduğundan regresyon modelinin bir bütün olarak istatistiksel olarak anlamlı olduğu sonucuna varıyoruz.

Model uyum tablosu:

R-Kare değeri bize, çalışılan saat sayısı ve girilen hazırlık sınavlarının sayısıyla açıklanabilecek sınav puanlarındaki değişimin yüzdesini verir.

Genel olarak, bir regresyon modelinin R-kare değeri ne kadar büyük olursa, yordayıcı değişkenlerin yanıt değişkeninin değerini tahmin etmede o kadar iyi olur.

Bu durumda sınav puanlarındaki farklılığın %73,4’ü çalışılan saat sayısı ve girilen hazırlık sınavı sayısı ile açıklanabilir.

Kök MSE değerinin bilinmesi de faydalıdır. Bu, gözlemlenen değerler ile regresyon çizgisi arasındaki ortalama mesafeyi temsil eder.

Bu regresyon modelinde gözlenen değerler regresyon doğrusundan ortalama 5,3657 birim sapmaktadır.

Parametre tahminleri tablosu:

Uygun regresyon denklemini yazmak için bu tablodaki parametre tahmin değerlerini kullanabiliriz:

Sınav puanı = 67.674 + 5.556*(saat) – 0.602*(hazırlık_sınavları)

Bu denklemi, bir öğrencinin çalışma saati ve girdiği deneme sınavı sayısına göre tahmini sınav puanını bulmak için kullanabiliriz.

Örneğin 3 saat ders çalışıp 2 hazırlık sınavına giren bir öğrencinin sınav puanının 83,1 olması gerekir:

Tahmini sınav puanı = 67,674 + 5,556*(3) – 0,602*(2) = 83,1

Saatlere ilişkin p değeri (<0,0001) 0,05’ten küçüktür, bu da sınav sonucuyla istatistiksel olarak anlamlı bir ilişkiye sahip olduğu anlamına gelir.

Ancak hazırlık sınavları için p değeri (0,5193) 0,05’ten az değildir, yani sınav sonucuyla istatistiksel olarak anlamlı bir ilişkisi yoktur.

İstatistiksel olarak anlamlı olmadıkları için hazırlık sınavlarını modelden çıkarmaya ve bunun yerine tek yordayıcı değişken olarak çalışılan saatleri kullanarak basit bir doğrusal regresyon gerçekleştirmeye karar verebiliriz.

Ek kaynaklar

Aşağıdaki eğitimlerde SAS’ta diğer ortak görevlerin nasıl gerçekleştirileceği açıklanmaktadır:

SAS’ta korelasyon nasıl hesaplanır?
SAS’ta basit doğrusal regresyon nasıl gerçekleştirilir?
SAS’ta tek yönlü ANOVA nasıl gerçekleştirilir?