Sas'ta temel bileşen analizi nasıl gerçekleştirilir?

Temel bileşen analizi (PCA), bir veri kümesindeki varyasyonun büyük bir bölümünü açıklayan temel bileşenleri (tahmin edici değişkenlerin doğrusal kombinasyonları) bulmayı amaçlayandenetimsiz bir makine öğrenme tekniğidir.

SAS’ta PCA gerçekleştirmenin en basit yolu, aşağıdaki temel sözdizimini kullanan PROC PRINCOMP deyimini kullanmaktır:

 proc princomp data =my_data out =out_data outstat =stats;
    var var1 var2 var3;
run ;

İşte her talimatın yaptığı şey:

• data : PCA için kullanılacak veri kümesinin adı
• out : Tüm orijinal verileri ve temel bileşen puanlarını içeren, oluşturulacak veri kümesinin adı
• outstat : Ortalamaları, standart sapmaları, korelasyon katsayılarını, özdeğerleri ve özvektörleri içeren bir veri kümesinin oluşturulması gerektiğini belirtir.
• var : giriş veri kümesinden PCA için kullanılacak değişkenler.

Aşağıdaki adım adım örnek, SAS’ta temel bileşenler analizi gerçekleştirmek için PROC PRINCOMP ifadesinin pratikte nasıl kullanılacağını gösterir.

1. Adım: Veri kümesi oluşturun

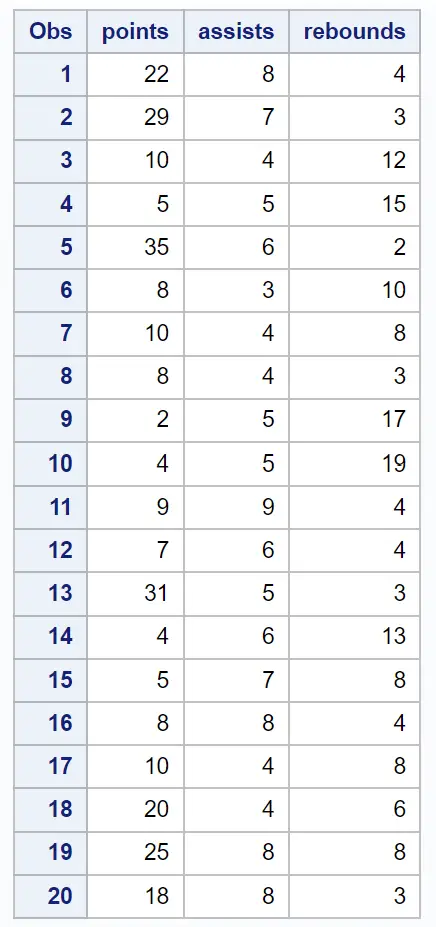
20 basketbol oyuncusu hakkında çeşitli bilgiler içeren aşağıdaki veri setine sahip olduğumuzu varsayalım:

 /*create dataset*/
data my_data;
    input points assists rebounds;
    datalines ;
22 8 4
29 7 3
10 4 12
5 5 15
35 6 2
8 3 10
10 4 8
8 4 3
2 5 17
4 5 19
9 9 4
7 6 4
31 5 3
4 6 13
5 7 8
8 8 4
10 4 8
20 4 6
25 8 8
18 8 3
;
run ;

/*view dataset*/
proc print data =my_data; 

Adım 2: Temel bileşenler analizini gerçekleştirin

Veri kümesinin noktaları , asistleri ve sıçrama değişkenlerini kullanarak temel bileşen analizini gerçekleştirmek için PROC PRINCOMP ifadesini kullanabiliriz:

 /*perform principal components analysis*/
proc princomp data =my_data out =out_data outstat =stats;
    var points assists rebounds;
run ;

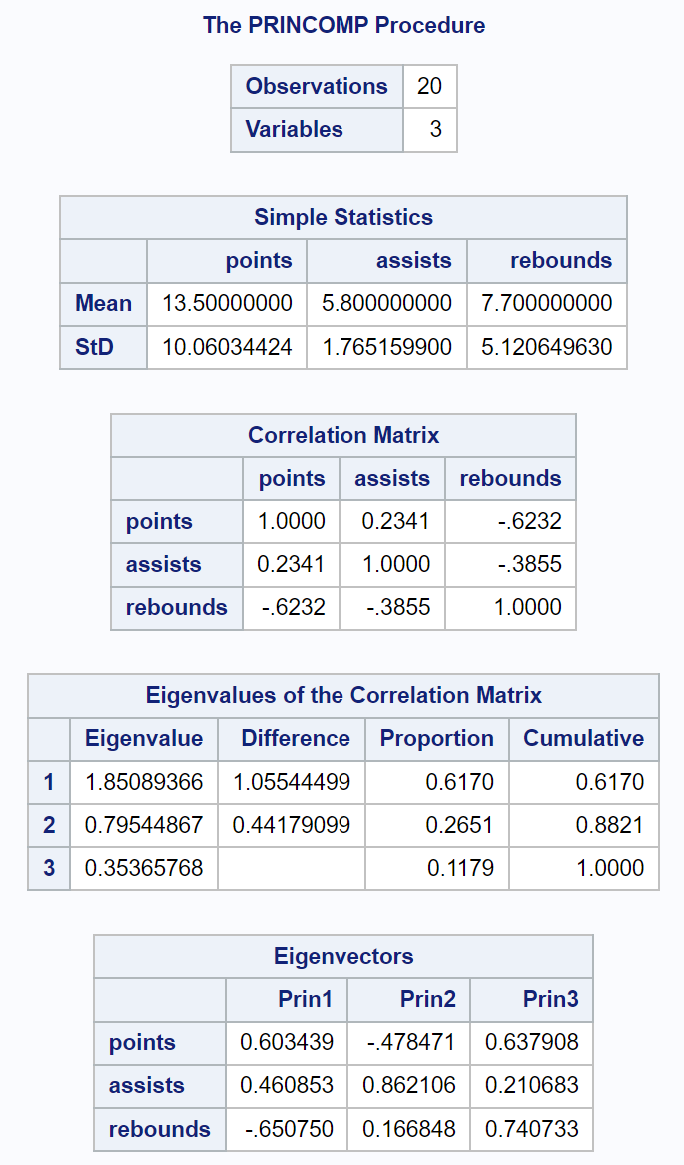
Çıktının ilk kısmı, her bir girdi değişkeninin ortalama ve standart sapmaları, bir korelasyon matrisi ve özdeğerlerin ve özvektörlerin değerleri dahil olmak üzere çeşitli tanımlayıcı istatistikleri görüntüler:

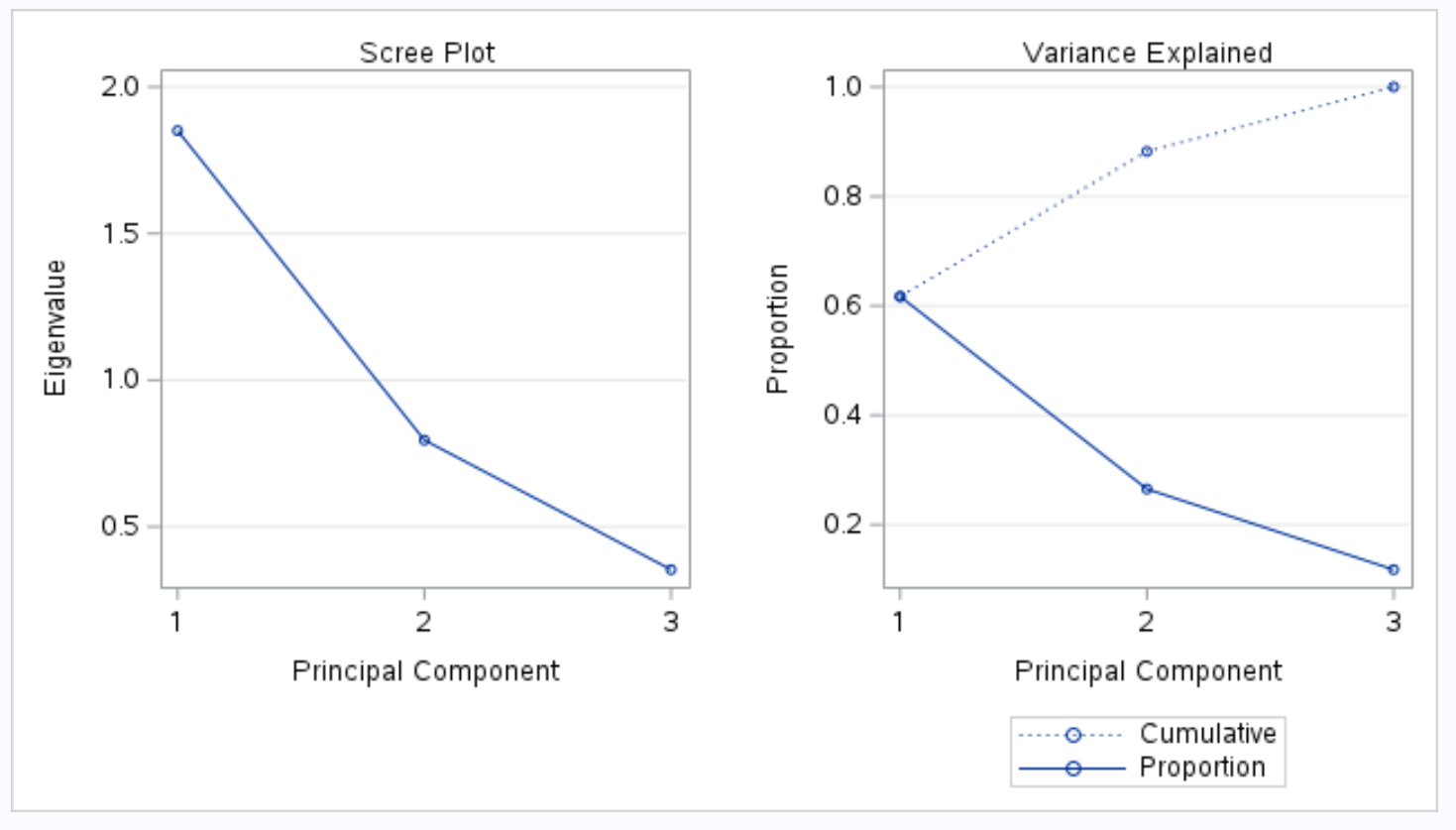
Çıktının bir sonraki bölümünde bir yamaç grafiği ve açıklanan varyans grafiği görüntülenir:

PCA uyguladığımızda genellikle veri setindeki toplam varyasyonun yüzde kaçının her bir temel bileşen tarafından açıklanabileceğini anlamak isteriz.

Ortaya çıkan Korelasyon Matrisi Özdeğerleri başlıklı tablo, her bir temel bileşen tarafından toplam varyasyonun yüzde kaçının açıklandığını tam olarak görmemizi sağlar:

• İlk temel bileşen, veri kümesindeki toplam varyasyonun %61,7’sini açıklıyor.
• İkinci temel bileşen veri setindeki toplam varyasyonun %26,51’ini açıklamaktadır.
• Üçüncü temel bileşen, veri setindeki toplam varyasyonun %11,79’unu açıklamaktadır.

Tüm yüzdelerin toplamının %100 olduğunu unutmayın.

Açıklanan Varyans başlıklı çizim bu değerleri görselleştirmemize olanak tanır.

X ekseni temel bileşeni görüntüler ve y ekseni, her bir temel bileşen tarafından açıklanan toplam varyansın yüzdesini görüntüler.

3. Adım: Sonuçları görselleştirmek için bir ikili grafik oluşturun

Belirli bir veri kümesi için PCA sonuçlarını görselleştirmek için, bir veri kümesindeki her gözlemi ilk iki ana bileşen tarafından oluşturulan bir düzlemde görüntüleyen bir çizim olan bir biplot oluşturabiliriz.

Bir biplot oluşturmak için SAS’ta aşağıdaki sözdizimini kullanabiliriz:

 /*create dataset with column called obs to represent row numbers of original data*/
data biplot_data;
   set out_data;
   obs=_n_;
run ;

/*create biplot using values from first two principal components*/
proc sgplot data =biplot_data;
    scatter x =Prin1 y =Prin2 / datalabel =obs;
run ; 

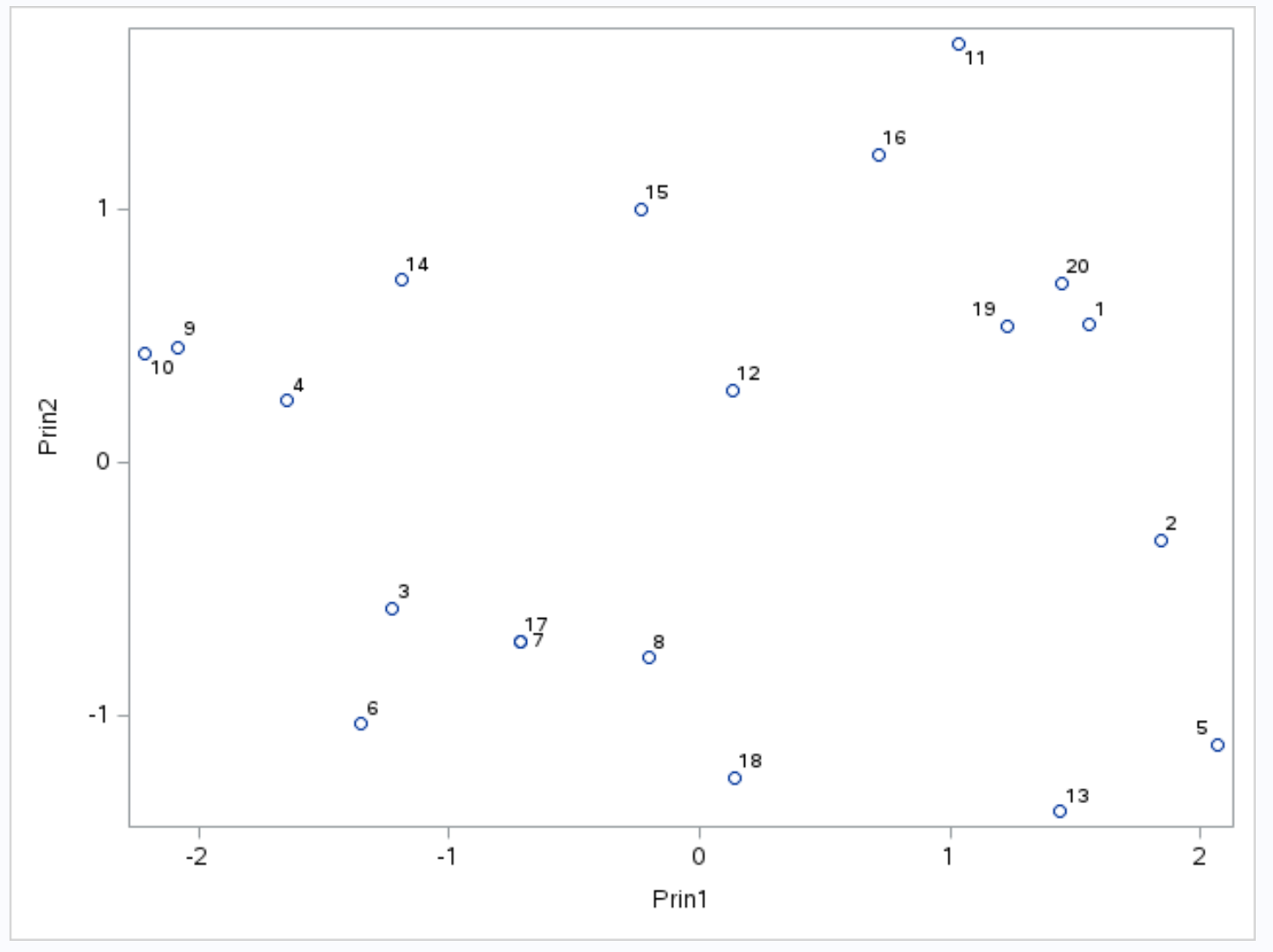
X ekseni birinci ana bileşeni, y ekseni ikinci ana bileşeni görüntüler ve veri kümesindeki bireysel gözlemler grafiğin içinde küçük daireler halinde görüntülenir.

Grafikte yan yana yer alan gözlemler sayı , asist ve ribaund olmak üzere üç değişken için de benzer değerlere sahip.

Örneğin grafiğin en solunda 9. ve 10. gözlemlerin birbirine son derece yakın olduğunu görebiliyoruz.

Orijinal veri setine başvurursak bu gözlemlere ilişkin şu değerleri görebiliriz:

• 9. Gözlem : 2 sayı, 5 asist, 17 ribaund
• Gözlem #10 : 4 sayı, 5 asist, 19 ribaund

Üç değişkenin her biri için değerler benzerdir, bu da bu gözlemlerin neden biplotta birbirine bu kadar yakın olduğunu açıklar.

Korelasyon Matrisi Özdeğerleri başlıklı sonuç tablosunda da ilk iki temel bileşenin veri setindeki toplam varyasyonun %88,21’ini oluşturduğunu gördük.

Bu yüzde çok yüksek olduğundan, iki noktadaki hangi gözlemlerin birbirine yakın olduğunu analiz etmek geçerlidir çünkü iki noktayı oluşturan iki temel bileşen, veri kümesindeki varyasyonun neredeyse tamamını açıklamaktadır.

Ek kaynaklar

Aşağıdaki eğitimlerde SAS’ta diğer ortak görevlerin nasıl gerçekleştirileceği açıklanmaktadır:

SAS’ta basit doğrusal regresyon nasıl gerçekleştirilir?
SAS’ta çoklu doğrusal regresyon nasıl gerçekleştirilir?
SAS’ta lojistik regresyon nasıl gerçekleştirilir?