R'de shapiro-wilk testi nasıl yapılır (örneklerle)

Shapiro-Wilk testi bir normallik testidir. Bir örneğin normal dağılımdan gelip gelmediğini belirlemek için kullanılır.

Bu test türü, belirli bir veri kümesinin normal dağılımdan gelip gelmediğini belirlemek için kullanışlıdır; bu, regresyon , ANOVA , t testleri ve diğerleri de dahil olmak üzere birçok istatistiksel testte yaygın olarak kullanılan bir varsayımdır. ‘diğerleri.

R’deki aşağıdaki yerleşik işlevi kullanarak belirli bir veri kümesi üzerinde Shapiro-Wilk testini kolayca gerçekleştirebiliriz:

shapiro.test(x)

Altın:

• x: veri değerlerinin sayısal bir vektörü.

Bu fonksiyon, karşılık gelen p değeriyle birlikte bir W testi istatistiği üretir. P değeri α = 0,05’ten küçükse, numunenin normal dağılıma sahip bir popülasyondan olmadığını söylemek için yeterli kanıt vardır.

Not: shapiro.test() işlevini kullanmak için örnek boyutu 3 ile 5.000 arasında olmalıdır.

Bu eğitimde bu işlevin pratik kullanımına ilişkin birkaç örnek gösterilmektedir.

Örnek 1: Normal veriler üzerinde Shapiro-Wilk testi

Aşağıdaki kod, örnek boyutu n=100 olan bir veri kümesinde Shapiro-Wilk testinin nasıl gerçekleştirileceğini gösterir:

 #make this example reproducible
set.seed(0)

#create dataset of 100 random values generated from a normal distribution
data <- rnorm(100)

#perform Shapiro-Wilk test for normality
shapiro.test(data)

	Shapiro-Wilk normality test

data:data
W = 0.98957, p-value = 0.6303

Testin p değeri 0,6303 olarak çıkıyor. Bu değer 0,05’ten küçük olmadığından örnek verilerin normal dağılıma sahip bir evrenden geldiğini varsayabiliriz.

Ortalama = 0 ve standart sapma = 1 olan bir normal dağılımdan rastgele değerler üreten rnorm() fonksiyonunu kullanarak örnek verileri oluşturduğumuz için bu sonuç şaşırtıcı olmamalıdır.

İlgili: R’de dnorm, pnorm, qnorm ve rnorm için bir kılavuz

Örnek verilerin normal şekilde dağıldığını görsel olarak doğrulamak için bir histogram da üretebiliriz:

 hist(data, col=' steelblue ') 

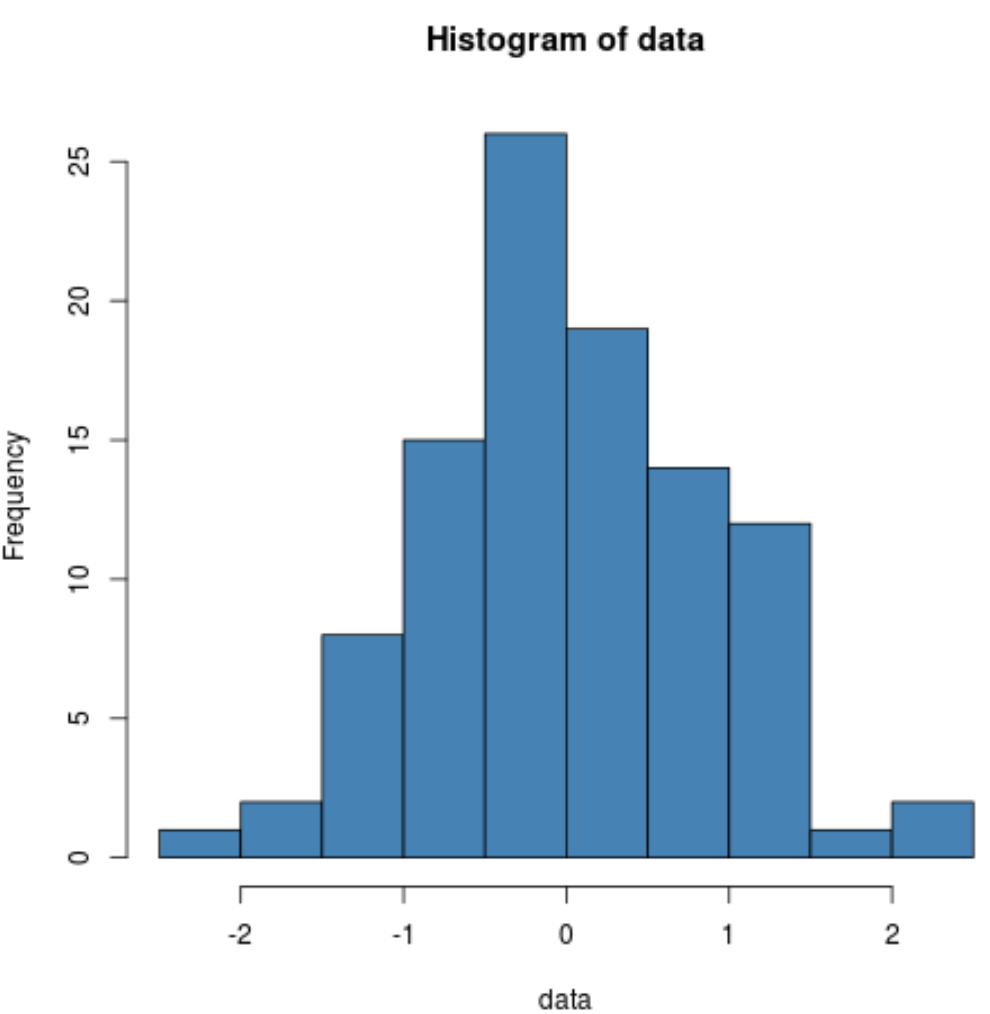
Dağılımın oldukça çan şeklinde olduğunu ve normal dağılmış verilerde tipik olan bir tepe noktasının dağılımın merkezinde olduğunu görebiliriz.

Örnek 2: Normal olmayan veriler üzerinde Shapiro-Wilk testi

Aşağıdaki kod, değerlerin bir Poisson dağılımından rastgele oluşturulduğu n=100 örneklem boyutuna sahip bir veri kümesi üzerinde Shapiro-Wilk testinin nasıl gerçekleştirileceğini gösterir:

 #make this example reproducible
set.seed(0)

#create dataset of 100 random values generated from a Poisson distribution
data <- rpois(n=100, lambda=3)

#perform Shapiro-Wilk test for normality
shapiro.test(data)

	Shapiro-Wilk normality test

data:data
W = 0.94397, p-value = 0.0003393

Testin p değeri 0,0003393 olarak çıkıyor. Bu değer 0,05’ten küçük olduğundan örneklem verilerinin normal dağılıma sahip bir evrenden gelmediğini söyleyebilecek yeterli kanıtımız vardır.

Örnek verileri bir Poisson dağılımından rastgele değerler üreten rpois() fonksiyonunu kullanarak oluşturduğumuz için bu sonuç şaşırtıcı olmamalıdır.

İlgili: R’de dpois, ppois, qpois ve rpois için bir kılavuz

Örnek verilerin normal şekilde dağılmadığını görsel olarak görmek için bir histogram da üretebiliriz:

 hist(data, col=' coral2 ') 

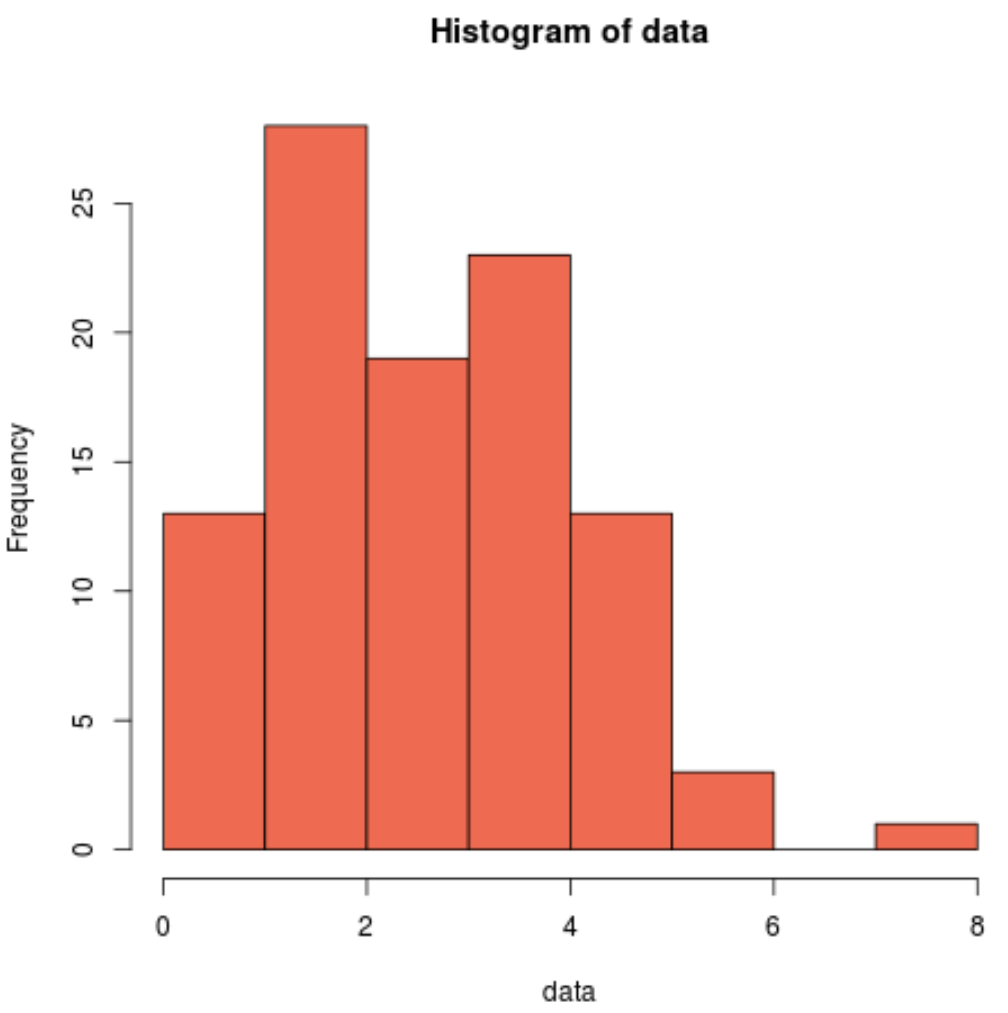
Dağılımın sağa çarpık olduğunu ve normal dağılımla ilişkilendirilen tipik “çan şekline” sahip olmadığını görebiliriz. Böylece histogramımız Shapiro-Wilk testinin sonuçlarıyla eşleşiyor ve örnek verilerimizin normal bir dağılımdan gelmediğini doğruluyor.

Normal olmayan verilerle ne yapılmalı

Belirli bir veri kümesi normal şekilde dağılmıyorsa , onu daha normal hale getirmek için sıklıkla aşağıdaki dönüşümlerden birini gerçekleştirebiliriz:

1. Günlük dönüşümü: yanıt değişkenini y’den log(y)’ ye dönüştürün.

2. Karekök dönüşümü: Yanıt değişkenini y’den √y’ye dönüştürün.

3. Küp kök dönüşümü: yanıt değişkenini y’den y ^1/3’e dönüştürün.

Bu dönüşümleri gerçekleştirerek, yanıt değişkeni genellikle normal dağılıma yaklaşır.

Bu dönüşümlerin pratikte nasıl gerçekleştirileceğini görmek için bu eğitime göz atın.

Ek kaynaklar

R’de Anderson-Darling testi nasıl yapılır?
R’de Kolmogorov-Smirnov testi nasıl yapılır?
Python’da Shapiro-Wilk Testi Nasıl Yapılır?