Ridge regresyonuna giriş

Sıradan çoklu doğrusal regresyonda , formun bir modeline uyacak şekilde bir dizi p tahmin değişkeni ve bir yanıt değişkeni kullanırız:

Y = β ₀ + β ₁ X _{1 +} β ₂ X ₂ + … + β _p

Altın:

• Y : Yanıt değişkeni
• X _j : ^j’inci tahmin değişkeni
• _βj : Diğer tüm belirleyicileri sabit tutarak, _Xj’deki bir birimlik artışın Y üzerindeki ortalama etkisi
• ε : Hata terimi

β ₀ , β ₁ , B ₂ , …, β _p değerleri, artıkların karelerinin toplamını (RSS) en aza indiren en küçük kareler yöntemi kullanılarak seçilir:

RSS = Σ(y _ben – ŷ _ben ) ²

Altın:

• Σ : Toplam anlamına gelen bir Yunan sembolü
• y _i : ^i’inci gözlem için gerçek yanıt değeri
• ŷ _i : Çoklu doğrusal regresyon modeline dayalı olarak tahmin edilen yanıt değeri

Ancak yordayıcı değişkenler yüksek düzeyde korelasyona sahip olduğunda çoklu doğrusallık bir sorun haline gelebilir. Bu, model katsayı tahminlerini güvenilmez hale getirebilir ve yüksek varyans sergileyebilir.

Belirli öngörücü değişkenleri modelden tamamen çıkarmadan bu sorunu çözmenin bir yolu, ridge regresyonu olarak bilinen ve bunun yerine aşağıdakileri en aza indirmeyi amaçlayan bir yöntem kullanmaktır:

RSS + λΣβ _j ²

burada j 1’den p’ye gider ve λ ≥ 0’dır.

Denklemdeki bu ikinci terim çekilme cezası olarak bilinir.

λ = 0 olduğunda, bu ceza teriminin hiçbir etkisi yoktur ve sırt regresyonu, en küçük kareler ile aynı katsayı tahminlerini üretir. Ancak λ sonsuza yaklaştıkça büzülme cezası daha etkili hale gelir ve tepe regresyon katsayısı tahminleri sıfıra yaklaşır.

Genel olarak, modeldeki en az etkili yordayıcı değişkenler en hızlı şekilde sıfıra doğru azalacaktır.

Neden Ridge Regresyonunu kullanmalısınız?

Ridge regresyonunun en küçük kareler regresyonuna göre avantajı önyargı-varyans değiş tokuşudur .

Ortalama Karesel Hatanın (MSE) belirli bir modelin doğruluğunu ölçmek için kullanabileceğimiz bir ölçüm olduğunu ve şu şekilde hesaplandığını hatırlayın:

MSE = Var( f̂( x ₀ )) + [Önyargı( f̂( x ₀ ))] ² + Var(ε)

MSE = Varyans + Önyargı ² + İndirgenemez hata

Ridge regresyonunun temel fikri, varyansın önemli ölçüde azaltılabilmesi ve böylece daha düşük bir genel MSE’ye yol açabilmesi için küçük bir önyargı eklemektir.

Bunu açıklamak için aşağıdaki grafiği inceleyin:

λ arttıkça sapmadaki çok küçük bir artışla varyansın önemli ölçüde azaldığını unutmayın. Ancak belirli bir noktadan sonra varyans daha yavaş azalır ve katsayılardaki azalma onların önemli ölçüde eksik tahmin edilmesine yol açar, bu da yanlılığın keskin bir şekilde artmasına neden olur.

Grafikten, λ için önyargı ve varyans arasında optimal bir denge sağlayan bir değer seçtiğimizde testin MSE’sinin en düşük olduğunu görebiliriz.

λ = 0 olduğunda, sırt regresyonundaki ceza teriminin hiçbir etkisi yoktur ve bu nedenle en küçük kareler ile aynı katsayı tahminlerini üretir. Ancak λ’yı belirli bir noktaya artırarak testin genel MSE’sini azaltabiliriz.

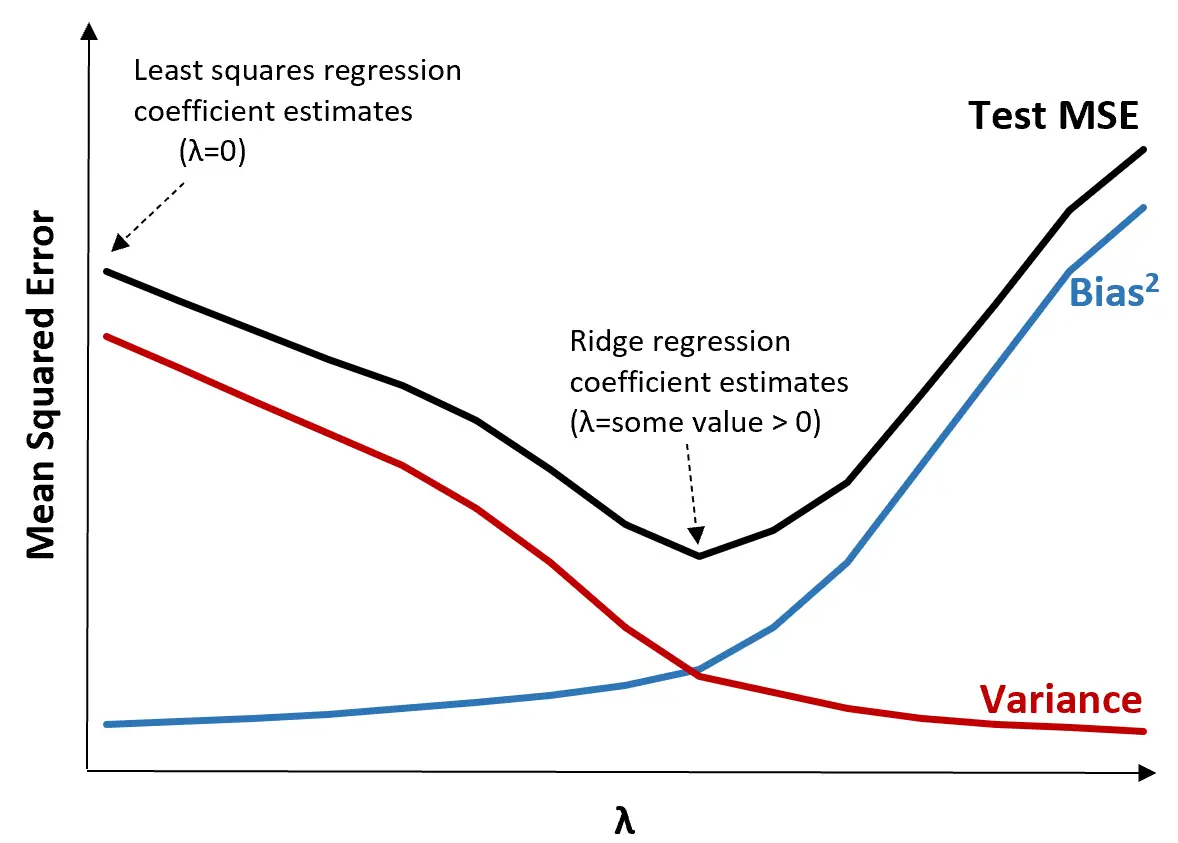
Bu, sırt regresyonuyla model uydurmanın, en küçük kareler regresyonuyla model uydurmaya göre daha küçük test hataları üreteceği anlamına gelir.

Uygulamada Ridge Regresyonunu Gerçekleştirme Adımları

Sırt regresyonunu gerçekleştirmek için aşağıdaki adımlar kullanılabilir:

Adım 1: Yordayıcı değişkenler için korelasyon matrisini ve VIF değerlerini hesaplayın.

Öncelikle bir korelasyon matrisi üretip her bir yordayıcı değişken için VIF (varyans enflasyon faktörü) değerlerini hesaplamamız gerekiyor.

Tahmin edici değişkenler ile yüksek VIF değerleri arasında güçlü bir korelasyon tespit edersek (bazı metinler “yüksek” VIF değerini 5 olarak tanımlarken diğerleri 10’u kullanır), o zaman ridge regresyonu muhtemelen uygundur.

Ancak verilerde çoklu bağlantı yoksa ilk etapta ridge regresyonu yapılması gerekmeyebilir. Bunun yerine sıradan en küçük kareler regresyonunu gerçekleştirebiliriz.

Adım 2: Her yordayıcı değişkeni standartlaştırın.

Ridge regresyonunu gerçekleştirmeden önce verileri, her öngörücü değişkenin ortalaması 0 ve standart sapması 1 olacak şekilde ölçeklendirmemiz gerekir. Bu, bir ridge regresyonu çalıştırırken hiçbir tek yordayıcı değişkenin aşırı bir etkiye sahip olmamasını sağlar.

Adım 3: Sırt regresyon modelini yerleştirin ve λ için bir değer seçin.

λ için hangi değerin kullanılacağını belirlemek için kullanabileceğimiz kesin bir formül yoktur. Pratikte λ’yı seçmenin iki yaygın yolu vardır:

(1) Bir Ridge izleme grafiği oluşturun. Bu, λ sonsuza doğru arttıkça katsayı tahminlerinin değerlerini görselleştiren bir grafiktir. Tipik olarak çoğu katsayı tahmininin istikrar kazanmaya başladığı değer olarak λ’yı seçeriz.

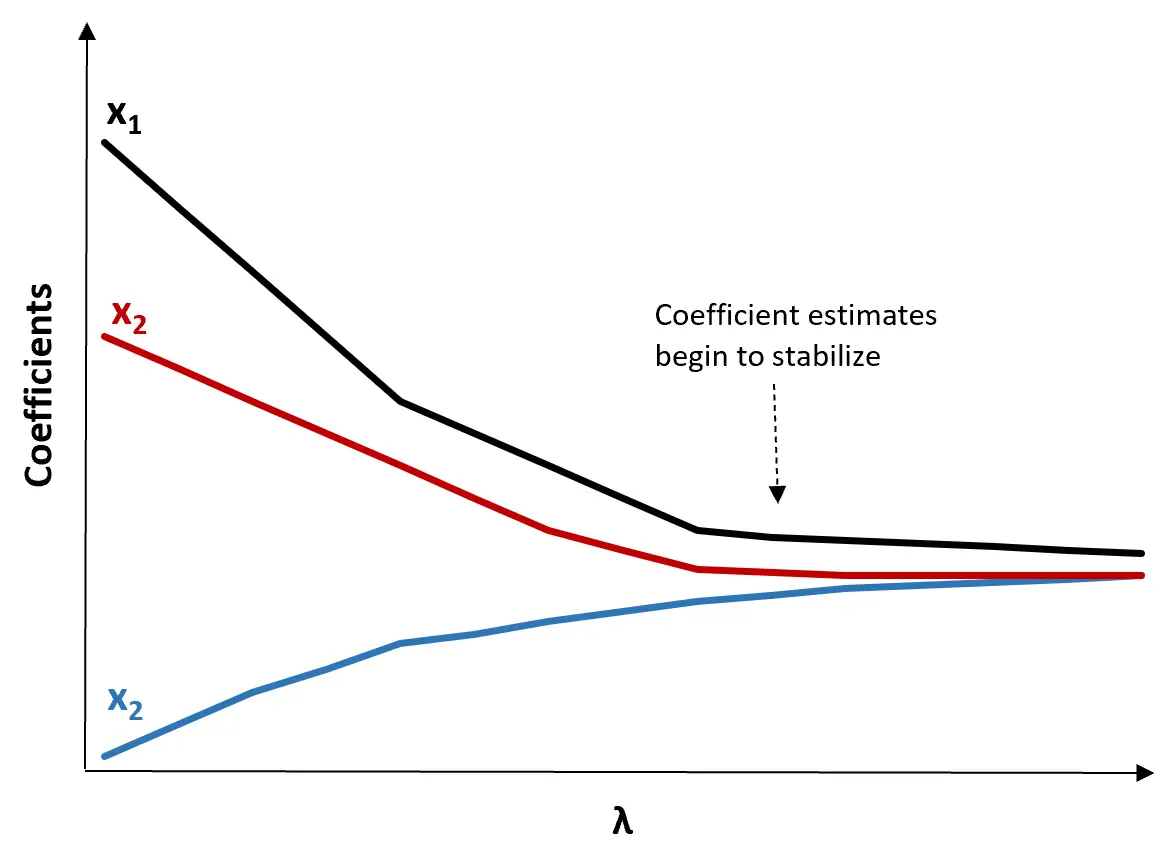
(2) Her λ değeri için MSE testini hesaplayın.

λ’yı seçmenin başka bir yolu, her modelin test MSE’sini farklı λ değerleri ile hesaplamak ve λ’yı en düşük test MSE’sini üreten değer olarak seçmektir.

Ridge Regresyonunun Avantajları ve Dezavantajları

Ridge regresyonunun en büyük avantajı , çoklu bağlantı mevcut olduğunda en küçük karelerden daha düşük bir test ortalama kare hatası (MSE) üretme yeteneğidir.

Ancak Ridge regresyonunun en büyük dezavantajı , tüm yordayıcı değişkenleri nihai modele dahil etmesi nedeniyle değişken seçimi yapamamasıdır. Bazı tahmin ediciler sıfıra çok yakın bir değere indirileceği için bu durum model sonuçlarının yorumlanmasını zorlaştırabilir.

Uygulamada Ridge regresyonu, en küçük kareler modeline kıyasla daha iyi tahminler yapabilen bir model üretme potansiyeline sahiptir, ancak modelin sonuçlarını yorumlamak genellikle daha zordur.

Model yorumlamanın mı yoksa tahmin doğruluğunun mu sizin için daha önemli olduğuna bağlı olarak, farklı senaryolarda sıradan en küçük kareler veya sırt regresyonunu kullanmayı seçebilirsiniz.

Ar-Ge ve Python’da Ridge Regresyon

Aşağıdaki eğitimler, ridge regresyon modellerini uydurmak için en yaygın kullanılan iki dil olan R ve Python’da ridge regresyonunun nasıl gerçekleştirileceğini açıklamaktadır:

R’de Ridge Regresyon (adım adım)
Python’da Ridge Regresyon (Adım Adım)