Snedecor f dağıtımı

İle Ağustos 4, 2023 Olasılık 0 Yorum

Bu makalede Snedecor F dağıtımının ne olduğu ve ne için kullanıldığı anlatılmaktadır. Ayrıca Snedecor F dağılım grafiğini ve istatistiksel özelliklerinin neler olduğunu görebileceksiniz.

Snedecor F dağılımı nedir?

Fisher-Snedecor F dağılımı veya basitçe F dağılımı olarak da adlandırılan Snedecor F dağılımı, istatistiksel çıkarımda, özellikle varyans analizinde kullanılan sürekli bir olasılık dağılımıdır.

Snedecor F dağılımının özelliklerinden biri, serbestlik derecelerini gösteren m ve n olmak üzere iki gerçek parametrenin değeriyle tanımlanmasıdır. Dolayısıyla Snedecor dağılımı F’nin sembolü Fm ,n’dir ; burada m ve n , dağılımı tanımlayan parametrelerdir.

F_{m,n}\qquad m,n>0″ title=”Rendered by QuickLaTeX.com” height=”18″ width=”139″ style=”vertical-align: -6px;”></p> </p> <p> Matematiksel olarak Snedecor F dağılımı, bir ki-kare dağılımı ile serbestlik dereceleri arasındaki bölümün, başka bir ki-kare dağılımı ile onun serbestlik dereceleri arasındaki bölüme bölünmesine eşittir. Böylece Snedecor F dağılımını tanımlayan formül aşağıdaki gibidir: </p> </p> <p class=\left.\begin{array}{c} X\sim \chi_m^2\\[2ex] Y\sim \chi_n^2\end{array}\right\}\color{orange}\bm{\longrightarrow}\color{black}\ F_{m,n}= \cfrac{X/m}{Y/n}

Fisher-Snedecor F dağılımı, adını İngiliz istatistikçi Ronald Fisher ve Amerikalı istatistikçi George Snedecor’dan almaktadır.

İstatistikte Fisher-Snedecor F dağılımının farklı uygulamaları vardır. Örneğin, Fisher-Snedecor F dağılımı farklı doğrusal regresyon modellerini karşılaştırmak için kullanılır ve bu olasılık dağılımı, varyans analizinde (ANOVA) kullanılır.

Snedecor F dağıtım şeması

Snedecor F dağılımının tanımını gördükten sonra yoğunluk fonksiyonunun grafiği ve kümülatif olasılık grafiği aşağıda gösterilmiştir.

Aşağıdaki grafikte farklı serbestlik derecelerine sahip Snedecor F dağılımlarının birkaç örneğini görebilirsiniz.

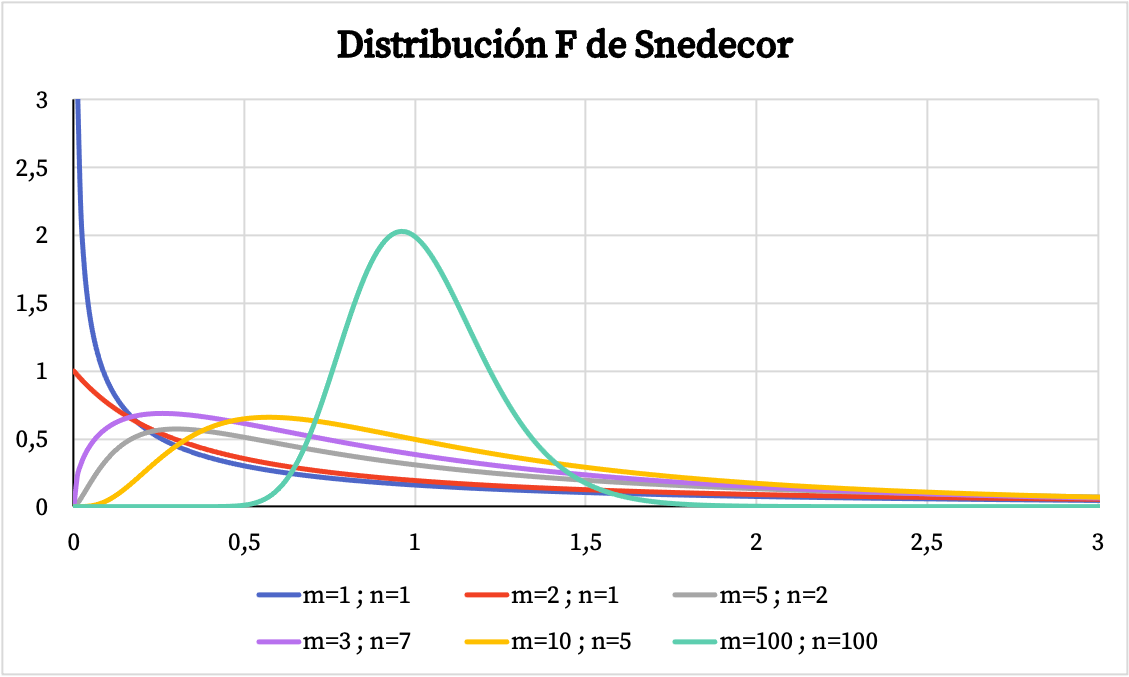
Snedecor F dağılım grafiği

Öte yandan aşağıdaki grafikte Snedecor F dağılımının kümülatif olasılık fonksiyonunun grafiğinin karakteristik değerlerine bağlı olarak nasıl değiştiğini görebilirsiniz.

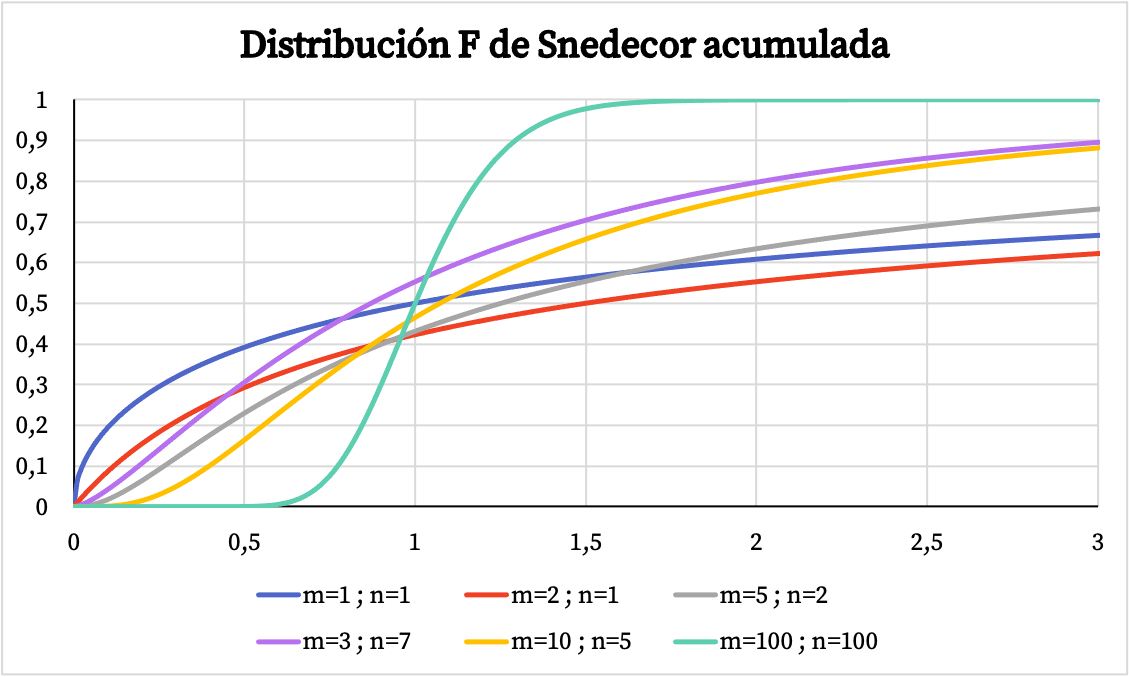
Snedecor F dağılımının kümülatif olasılığı

Snedecor F dağılımının özellikleri

Son olarak bu bölümde Snedecor F dağılımının en önemli özellikleri sunulmaktadır.

  • Snedecor F dağılımının serbestlik dereceleri, m ve n , dağılımın şeklini tanımlayan iki parametredir. Snedecor F dağılımının bu karakteristik değerleri pozitif tamsayılardır.

\begin{array}{c}m,n \in \mathbb{Z}\\[2ex] m,n>0\end{array}” title=”Rendered by QuickLaTeX.com” height=”54″ width=”68″ style=”vertical-align: 0px;”></p> </p> <ul> <li> Snedecor F dağılımının alanı sıfırdan büyük veya sıfıra eşit tüm gerçek sayılardan oluşur.</li> </ul> <p class=x\in [0,+\infty)

  • n’nin 2’den büyük değerleri için Snedecor F dağılımının ortalaması, n eksi 2’nin çıkarılmasıyla n’ye eşittir.

\begin{array}{c}X\sim F_{m,n}\\[2ex] E[X]=\cfrac{n}{n-2} \qquad \text{para }n>2\end{array} ” title=”Rendered by QuickLaTeX.com” height=”75″ width=”225″ style=”vertical-align: 0px;”></p> </p> <ul> <li> <em>n</em> parametresi 2’den büyük olduğunda Snedecor dağılımı F’nin varyansı aşağıdaki formül uygulanarak hesaplanabilir:</li> </ul> <p class=\begin{array}{c}X\sim F_{m,n}\\[2ex] Var(X)=\cfrac{2n^2\cdot (m+n-2)}{m\cdot (n-2)^2\cdot (n-4)} \qquad \text{para }n>4\end{array} ” title=”Rendered by QuickLaTeX.com” height=”80″ width=”366″ style=”vertical-align: 0px;”></p> </p> <ul> <li> Eğer <em>m</em> parametresi 2’den büyükse, Snedecor dağılımı F’nin modu aşağıdaki ifadeyle hesaplanabilir:</li> </ul> <p class=Mo=\cfrac{m-2}{m}\cdot \cfrac{n}{n+2}\qquad \text{para }m>2″ title=”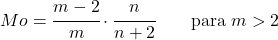Rendered by QuickLaTeX.com” height=”40″ width=”278″ style=”vertical-align: -14px;”></p> </p> <ul> <li> Snedecor dağılımı F’nin yoğunluk fonksiyonu formülü aşağıdaki gibidir:</li> </ul> <p class=\displaystyle P[X=x]=\frac{\Gamma\left(\frac{m+n}{2}\right)}{\Gamma\left(\frac{m}{2}\right)\Gamma\left(\frac{n}{2}\right)}\left(\frac{m}{n}\right)^{\frac{m}{2}}\cdot\frac{x^{\frac{m-2}{2}}}{\left(1+\frac{mx}{n}\right)^{\frac{m+n}{2}}}

  • Bir değişken, m ve n serbestlik derecelerine sahip bir Snedecor F dağılımını takip ediyorsa, söz konusu değişkenin tersi, aynı serbestlik derecesine sahip ancak değerlerinin sırası değişen bir Snedecor F dağılımını takip eder.

X\sim F_{m,n} \ \color{orange}\bm{\longrightarrow}\color{\black} \ X^{-1}\sim F_{n,m}

  • Öğrenci dağılımı Snedecor F dağılımı ile aşağıdaki ilişkiye sahiptir:

X\sim t_n \ \color{orange}\bm{\longrightarrow}\color{\black} \ X^2\sim F_{1,n}

yazar hakkında

Dr.Benjamin Anderson
Dr.benjamin anderson

Merhaba, ben Benjamin, emekli bir istatistik profesörü ve Statorials öğretmenine dönüştüm. İstatistik alanındaki kapsamlı deneyimim ve uzmanlığımla, öğrencilerimi Statorials aracılığıyla güçlendirmek için bilgilerimi paylaşmaya can atıyorum. Daha fazlasını bil

Yorum ekle

E-posta hesabınız yayımlanmayacak. Gerekli alanlar * ile işaretlenmişlerdir