Spearman sıralama korelasyonu ne zaman kullanılmalı (2 senaryo)

İki değişken arasındaki doğrusal ilişkiyi ölçmenin en yaygın yolu, her zaman -1 ile 1 arasında bir değer alan Pearson korelasyon katsayısını kullanmaktır ; burada:

• -1 tamamen negatif bir doğrusal korelasyonu gösterir
• 0 doğrusal korelasyonun olmadığını gösterir
• 1 mükemmel pozitif doğrusal korelasyonu gösterir

Bununla birlikte, bu tür bir korelasyon katsayısı, iki değişken arasındaki gerçek temel ilişkinin doğrusal olduğu durumlarda en iyi sonucu verir.

İki spesifik senaryoda en iyi şekilde kullanılan , Spearman sıralama korelasyonu adı verilen başka bir tür korelasyon katsayısı daha vardır:

Senaryo 1 : Gizli verilerle çalışırken.

• Bir öğrencinin matematik sınavı puanı sıralamasının yanı sıra bir sınıftaki fen sınavı puanı sıralamasını da içeren bir veri kümesi buna örnek olarak verilebilir.

Senaryo 2 : Bir veya daha fazla aşırı aykırı değer mevcut olduğunda.

• Bir veri setinde aşırı aykırı değerler mevcut olduğunda Pearson korelasyon katsayısı büyük ölçüde etkilenir.

Aşağıdaki örnekler, bu senaryoların her birinde Spearman sıra korelasyonunun nasıl hesaplanacağını göstermektedir.

Senaryo 1: Spearman Sıralamasını Dereceli Verilerle İlişkilendirmek

İki değişken arasındaki ilişkiyi gösteren aşağıdaki veri setini (ve karşılık gelen dağılım grafiğini) göz önünde bulundurun:

İstatistik yazılımı kullanarak bu iki değişken için aşağıdaki korelasyon katsayılarını hesaplayabiliriz:

• Pearson korelasyonu: 0,79
• Spearman sıralama korelasyonu: 1

Bu senaryoda, veri değerlerinin sadece sıralamasını önemsiyorsak (x’in sırası arttıkça y’nin sırası da artar mı?), Spearman’ın sıra korelasyonu bize daha iyi bir fikir verecektir. iki değişken arasındaki korelasyon. .

Bu özel veri setinde x’in rütbesi arttıkça y’nin rütbesi de her zaman artar.

Spearman’ın sıra korelasyonu, x’in sıraları ile y’nin sıraları arasında mükemmel bir pozitif ilişki ( ρ = 1 ) olduğunu söyleyerek bu davranışı mükemmel bir şekilde yakalar.

Öte yandan Pearson korelasyonu bize iki değişken arasında güçlü bir doğrusal ilişki ( r = 0,79 ) olduğunu söyler.

Bu doğrudur, ancak yalnızca x’in mertebeleri ile y’nin mertebeleri arasındaki ilişkiyi önemsiyorsak yararlı değildir.

Senaryo 2: Spearman sıralamasının aşırı aykırı değerlerle korelasyonu

İki değişken arasındaki ilişkiyi gösteren aşağıdaki veri setini (ve karşılık gelen dağılım grafiğini) göz önünde bulundurun:

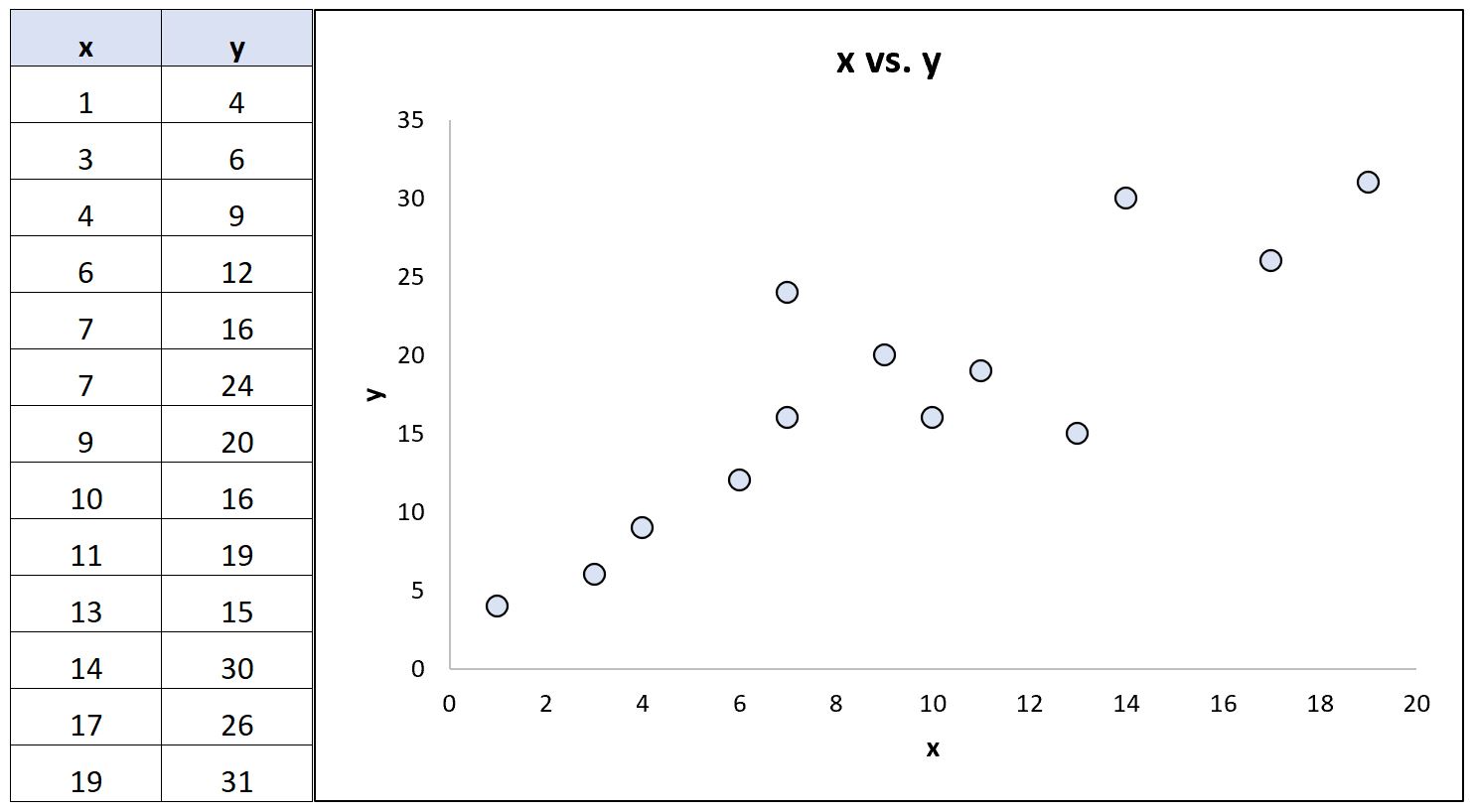
İstatistik yazılımı kullanarak bu iki değişken için aşağıdaki korelasyon katsayılarını hesaplayabiliriz:

• Pearson korelasyonu: 0,86
• Spearman sıralama korelasyonu: 0,85

Korelasyon katsayıları neredeyse aynıdır çünkü değişkenler arasındaki temel ilişki yaklaşık olarak doğrusaldır ve aşırı aykırı değerler yoktur.

Şimdi veri kümesindeki son y değerini aşırı uç değer olacak şekilde değiştirdiğimizi varsayalım:

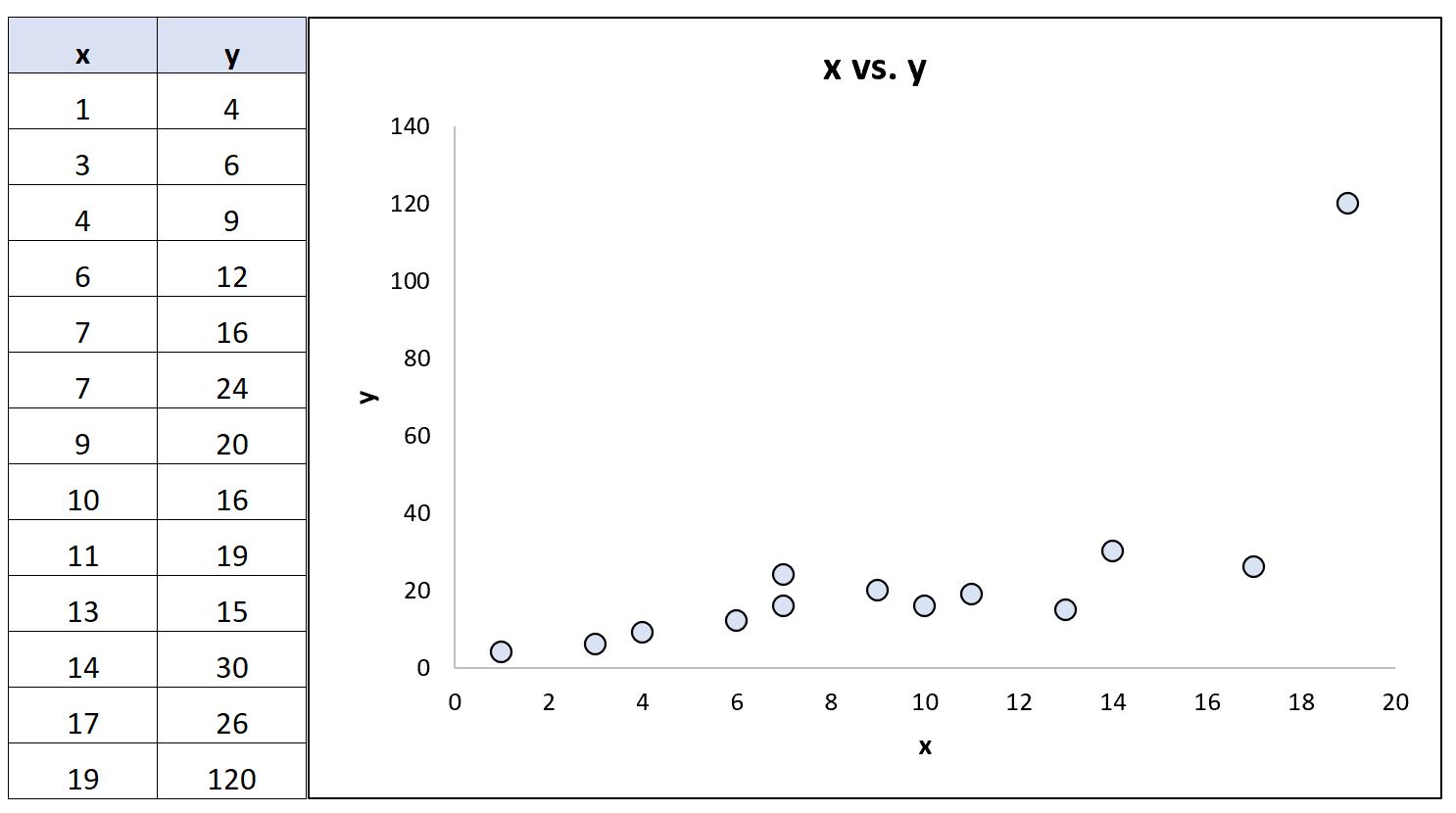
İstatistik yazılımı kullanarak korelasyon katsayılarını yeniden hesaplayabiliriz:

• Pearson korelasyonu: 0,69
• Spearman sıralama korelasyonu: 0,85

Pearson korelasyon katsayısı önemli ölçüde değişirken Spearman sıra korelasyon katsayısı aynı kaldı.

İstatistik jargonunu kullanırsak, x ve y arasındaki ilişkinin monoton olduğunu (x arttıkça y genellikle artar) ancak aykırı değerin verileri büyük ölçüde etkilediği için doğrusal olmadığını söyleyebiliriz.

Bu senaryoda, Spearman’ın sıra korelasyonu bu monotonik ilişkiyi iyi bir şekilde ölçerken, Pearson korelasyonu iki değişken arasındaki doğrusal ilişkiyi hesaplamaya çalıştığı için kötü bir iş çıkarıyor.

İlgili: Spearman Sıralaması Korelasyonunu APA Formatında Raporlama

Ek kaynaklar

Aşağıdaki eğitimlerde farklı yazılımlar kullanılarak Spearman sıra korelasyonunun nasıl hesaplanacağı açıklanmaktadır:

Excel’de Spearman Sıra Korelasyonu Nasıl Hesaplanır?
Google E-Tablolarda Spearman Sıra Korelasyonu Nasıl Hesaplanır?
R’de Spearman sıralama korelasyonu nasıl hesaplanır
Python’da Spearman Sıra Korelasyonu Nasıl Hesaplanır?