Google e-tablolarda spearman sıralaması korelasyonu nasıl hesaplanır?

İstatistikte korelasyon , iki değişken arasındaki ilişkinin gücünü ve yönünü ifade eder. Bir korelasyon katsayısının değeri, aşağıdaki yorumlara göre -1 ile 1 arasında değişebilir:

• -1: iki değişken arasında mükemmel bir negatif ilişki
• 0: iki değişken arasında ilişki yok
• 1: iki değişken arasında mükemmel bir pozitif ilişki

Özel bir korelasyon türü, iki sıralı değişken arasındaki korelasyonu ölçmek için kullanılan Spearman’ın sıra korelasyonu olarak adlandırılır. (örneğin, bir öğrencinin matematik sınavı puanının, sınıftaki fen bilimleri sınavı puanına göre sıralaması).

Bu eğitimde, Google E-Tablolar’da iki değişken arasındaki Spearman sıralama korelasyonunun nasıl hesaplanacağı açıklanmaktadır.

Örnek: Google E-Tablolar’daki Spearman Sıralaması Korelasyonu

Belirli bir sınıftaki 10 öğrencinin matematik sınavı puanı ile fen sınavı puanı arasındaki Spearman sıra korelasyonunu hesaplamak için aşağıdaki adımları uygulayın.

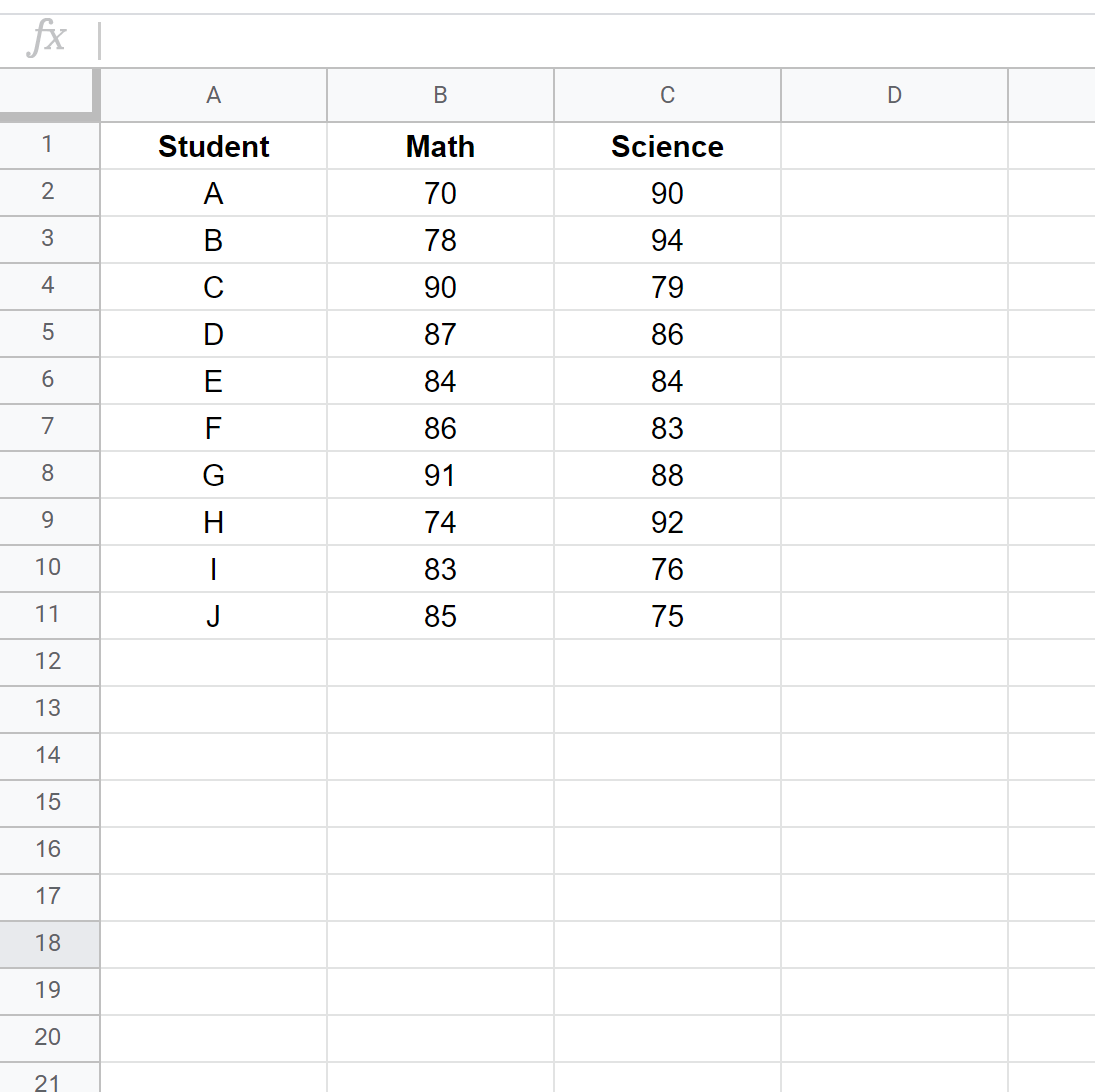
Adım 1: Verileri girin.

Her öğrencinin sınav sonuçlarını iki ayrı sütuna girin:

Adım 2: Her sınav puanı için sıralamayı hesaplayın.

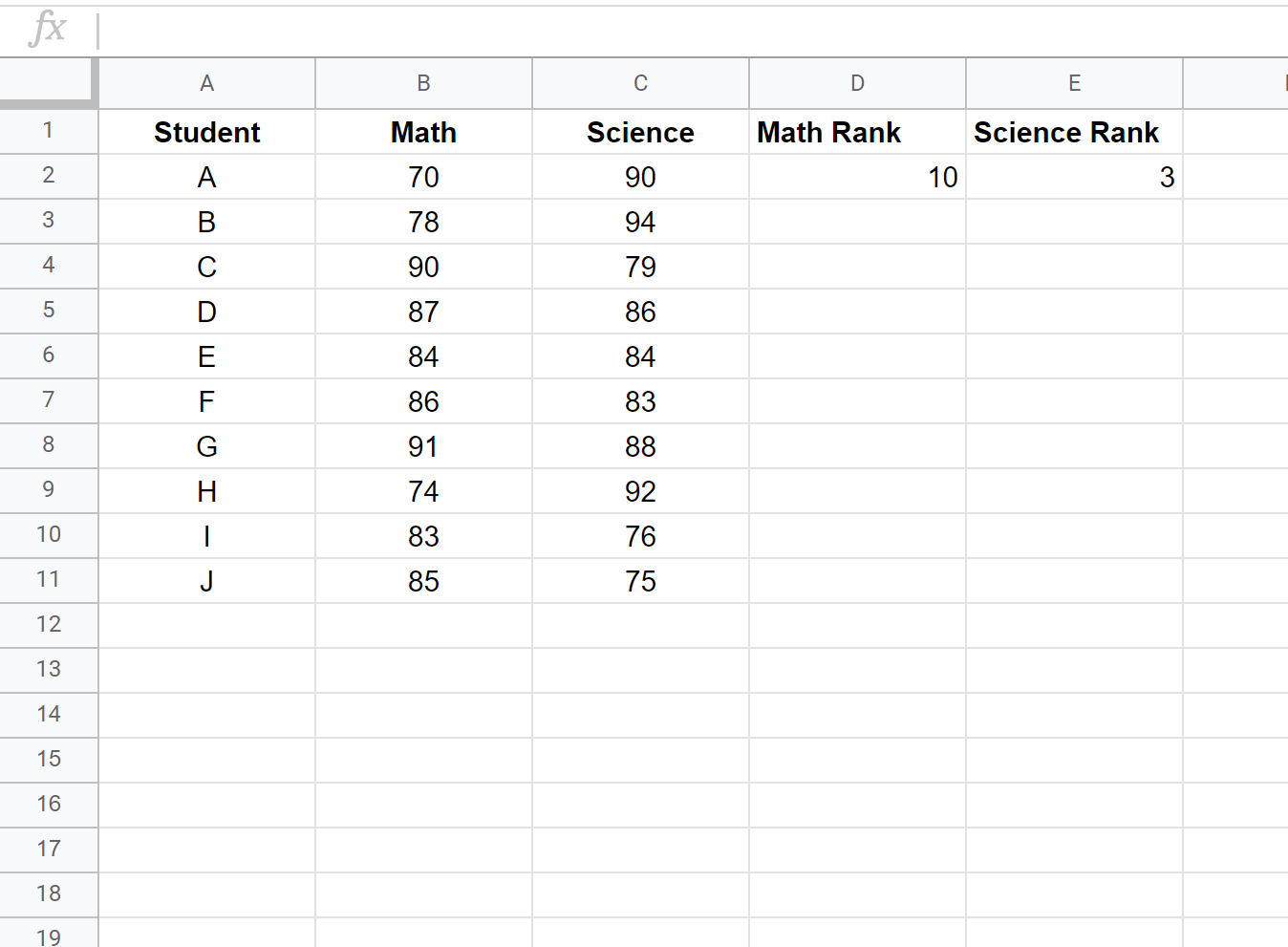
Daha sonra her sınav puanı için sıralamayı hesaplayacağız. Birinci öğrencinin matematik ve fen bilimleri sıralamasını hesaplamak için D2 ve E2 hücrelerinde aşağıdaki formülleri kullanın:

Hücre D2: =RANK.ORT(B2, $B$2:$B$11, 0)

Hücre E2: =RANK.ORT(C2, $C$2:$C$11, 0)

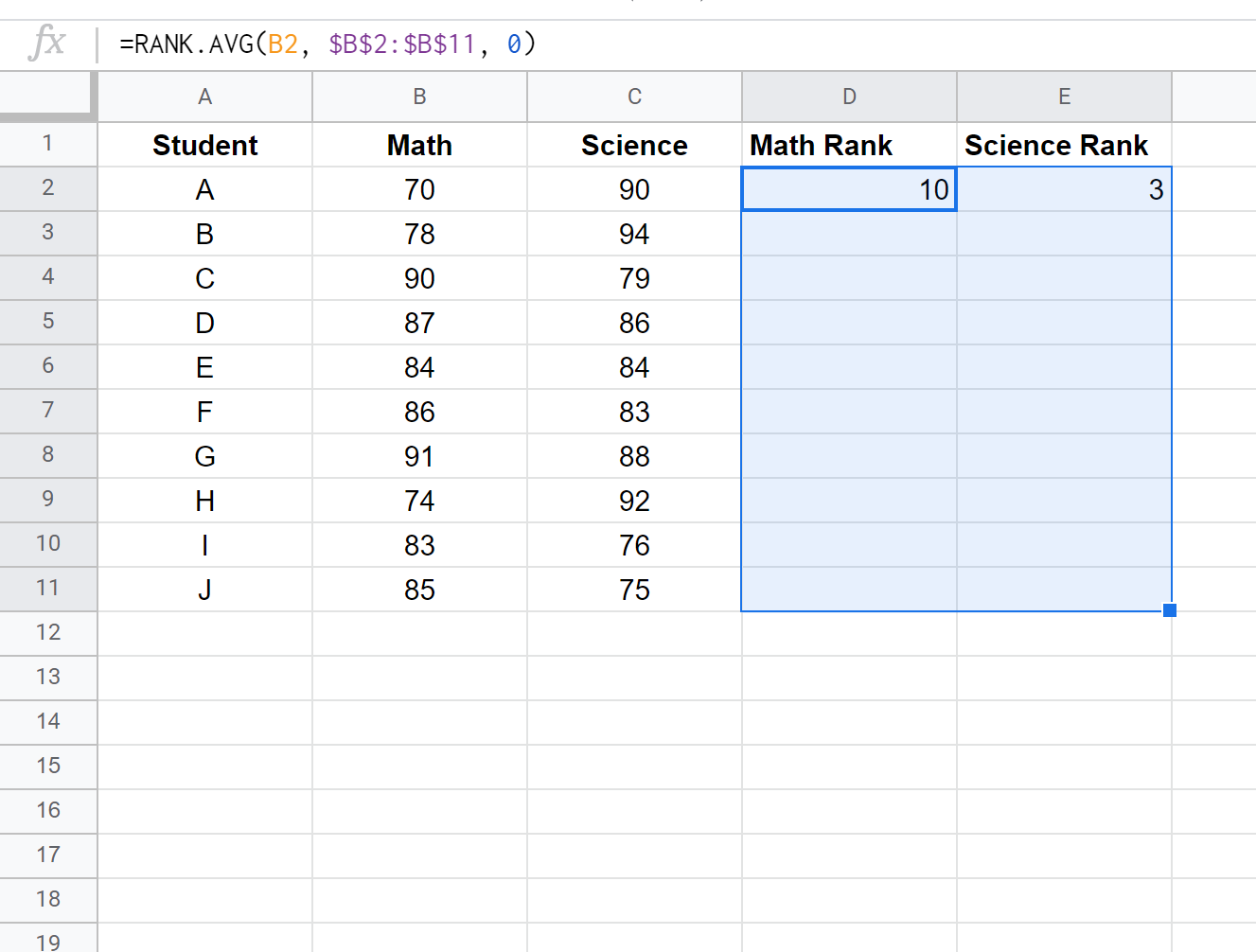
Ardından doldurulacak kalan hücreleri vurgulayın:

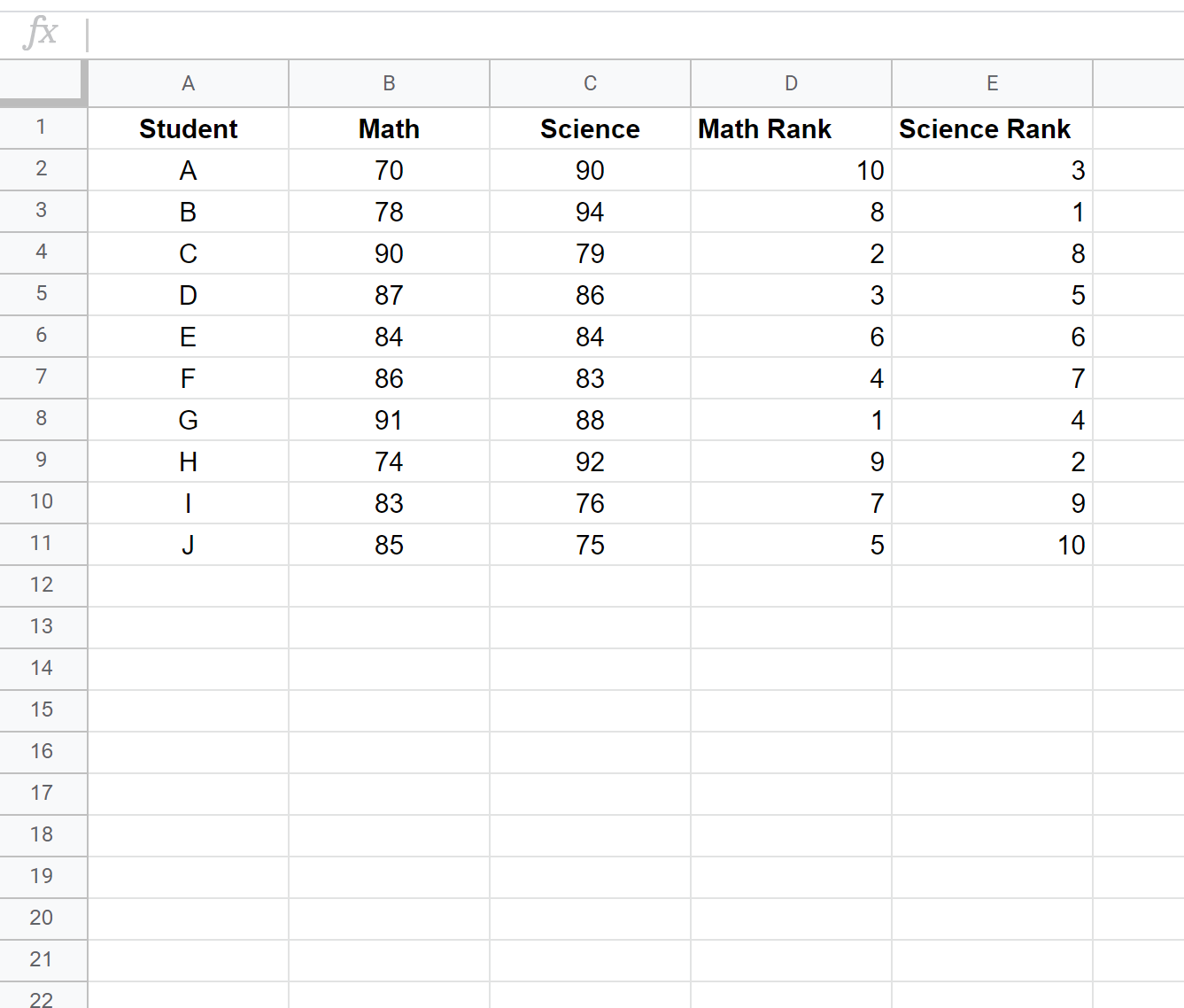
Daha sonra her öğrencinin sıralamasını girmek için Ctrl+D tuşlarına tıklayın:

Adım 3: Spearman sıra korelasyon katsayısını hesaplayın.

Son olarak matematik puanları ile fen bilimleri puanları arasındaki Spearman sıra korelasyon katsayısını CORREL() fonksiyonunu kullanarak hesaplayacağız:

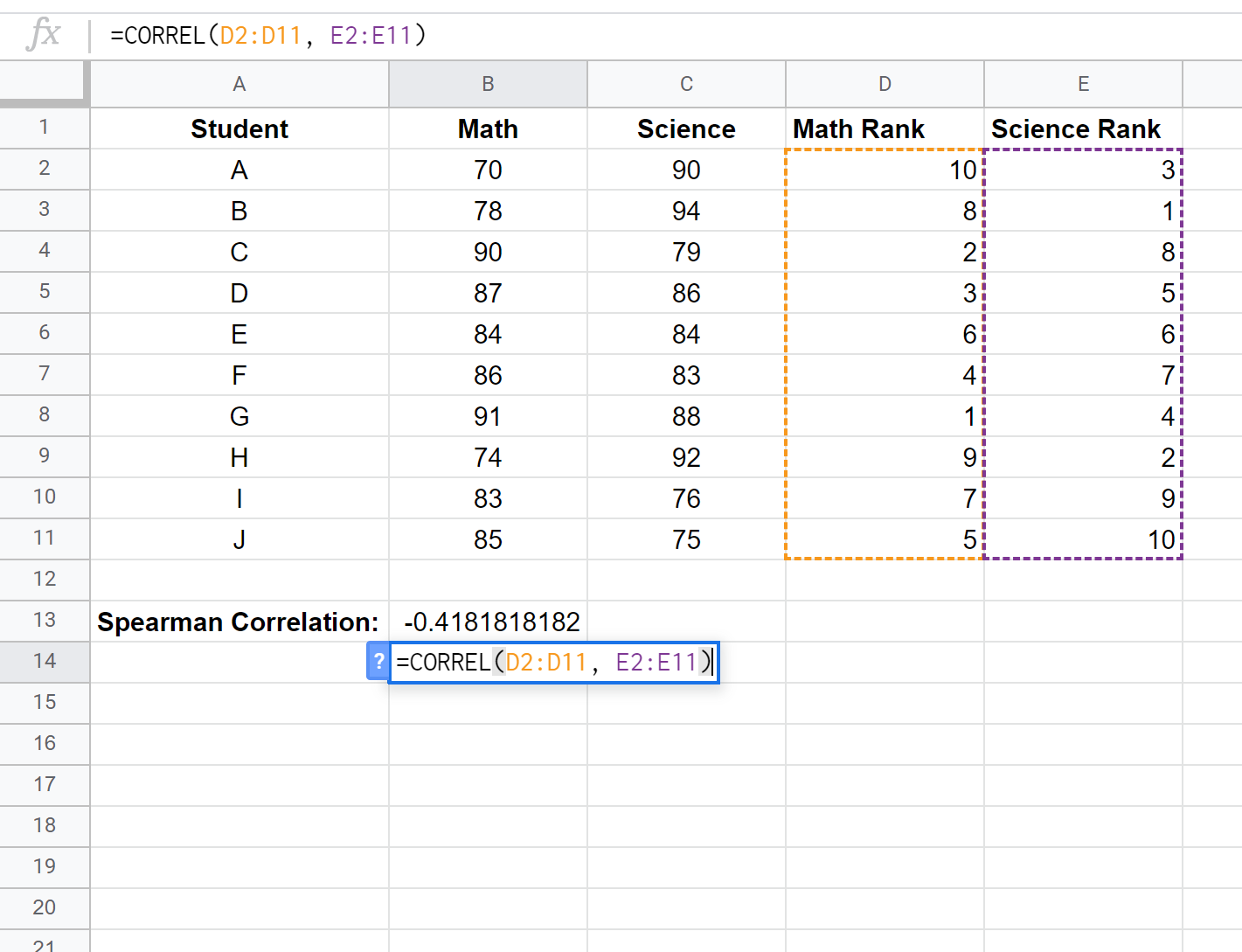
Spearman sıra korelasyonu -0,41818 olarak ortaya çıkıyor.

Adım 4 (İsteğe Bağlı): Spearman sıra korelasyonunun istatistiksel olarak anlamlı olup olmadığını belirleyin.

Önceki adımda, matematik ve fen bilimleri sınav puanları arasındaki Spearman sıra korelasyonunun -0,41818 olduğunu bulduk; bu, iki değişken arasında negatif bir korelasyon olduğunu gösteriyor.

Bununla birlikte, bu korelasyonun istatistiksel olarak anlamlı olup olmadığını belirlemek için, farklı örneklem boyutları (n) ve anlamlılık düzeyleri (α) ile ilişkili kritik değerleri gösteren kritik değerlerin Spearman sıra korelasyon tablosuna başvurmamız gerekir.

Korelasyon katsayımızın mutlak değeri tablodaki kritik değerden büyükse iki değişken arasındaki korelasyon istatistiksel olarak anlamlıdır.

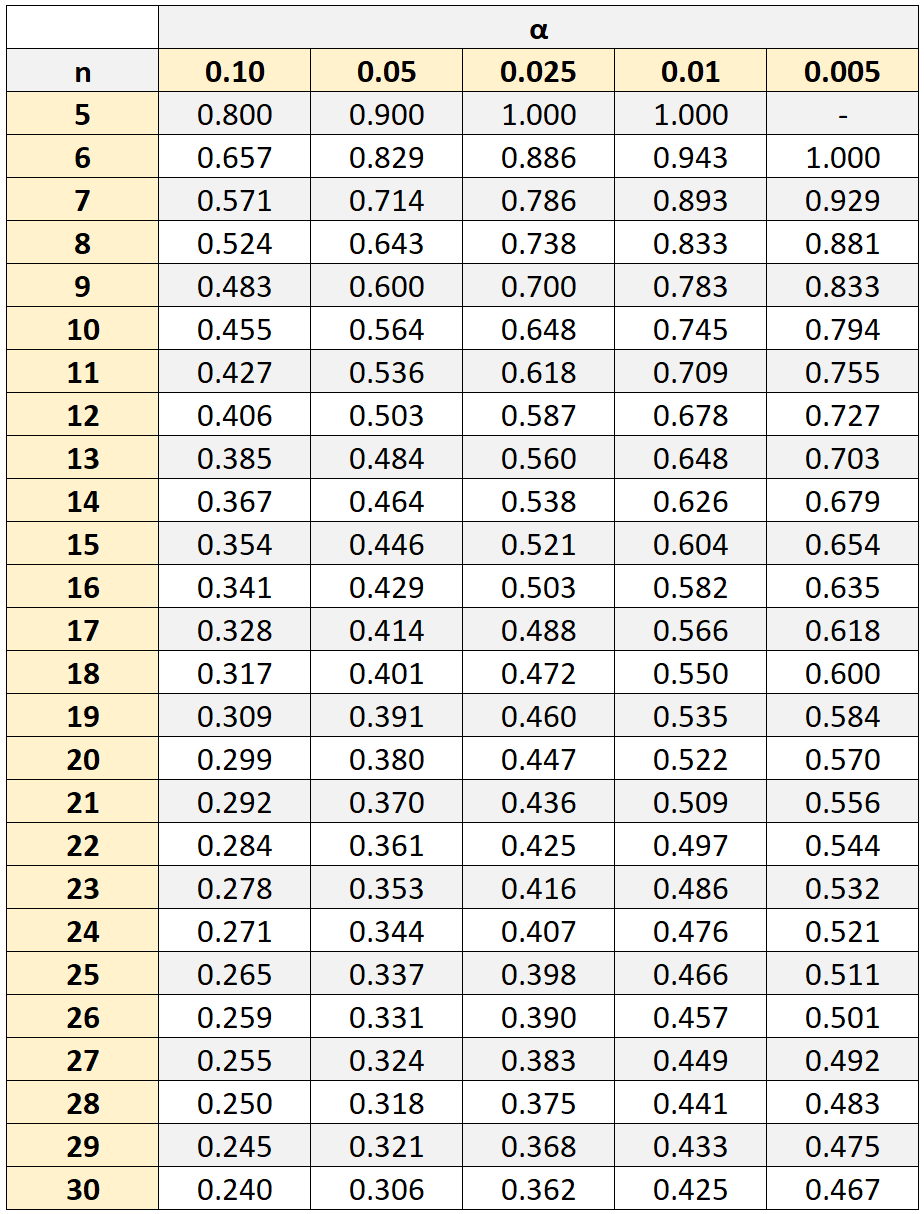
Örneğimizde örneklem büyüklüğümüz n = 10 öğrenciydi. 0,05 anlamlılık düzeyini kullanarak kritik değerin 0,564 olduğunu buluyoruz.

Hesapladığımız Spearman sıra korelasyon katsayısının mutlak değeri ( 0,41818 ) bu kritik değerden büyük olmadığı için matematik ve fen bilimleri puanları arasındaki korelasyonun istatistiksel olarak anlamlı olmadığı anlamına gelmektedir.

İlgili: Excel’de Spearman Sıra Korelasyonu Nasıl Hesaplanır?