Spss'de ikinci dereceden regresyon nasıl gerçekleştirilir?

İki değişkenin doğrusal bir ilişkisi olduğunda, ilişkilerini ölçmek için sıklıkla basit doğrusal regresyonu kullanabilirsiniz .

Ancak basit doğrusal regresyon, iki değişkenin doğrusal olmayan bir ilişkisi olduğunda iyi çalışmaz. Bu durumlarda ikinci dereceden regresyonu kullanmayı deneyebilirsiniz.

Bu eğitimde SPSS’de ikinci dereceden regresyonun nasıl gerçekleştirileceği açıklanmaktadır.

Örnek: SPSS’de İkinci Dereceden Regresyon

Çalışılan saat sayısı ile mutluluk arasındaki ilişkiyi anlamak istediğimizi varsayalım. 16 farklı kişi için haftalık çalışılan saat sayısı ve rapor edilen mutluluk düzeyi (0’dan 100’e kadar bir ölçekte) hakkında aşağıdaki verilere sahibiz:

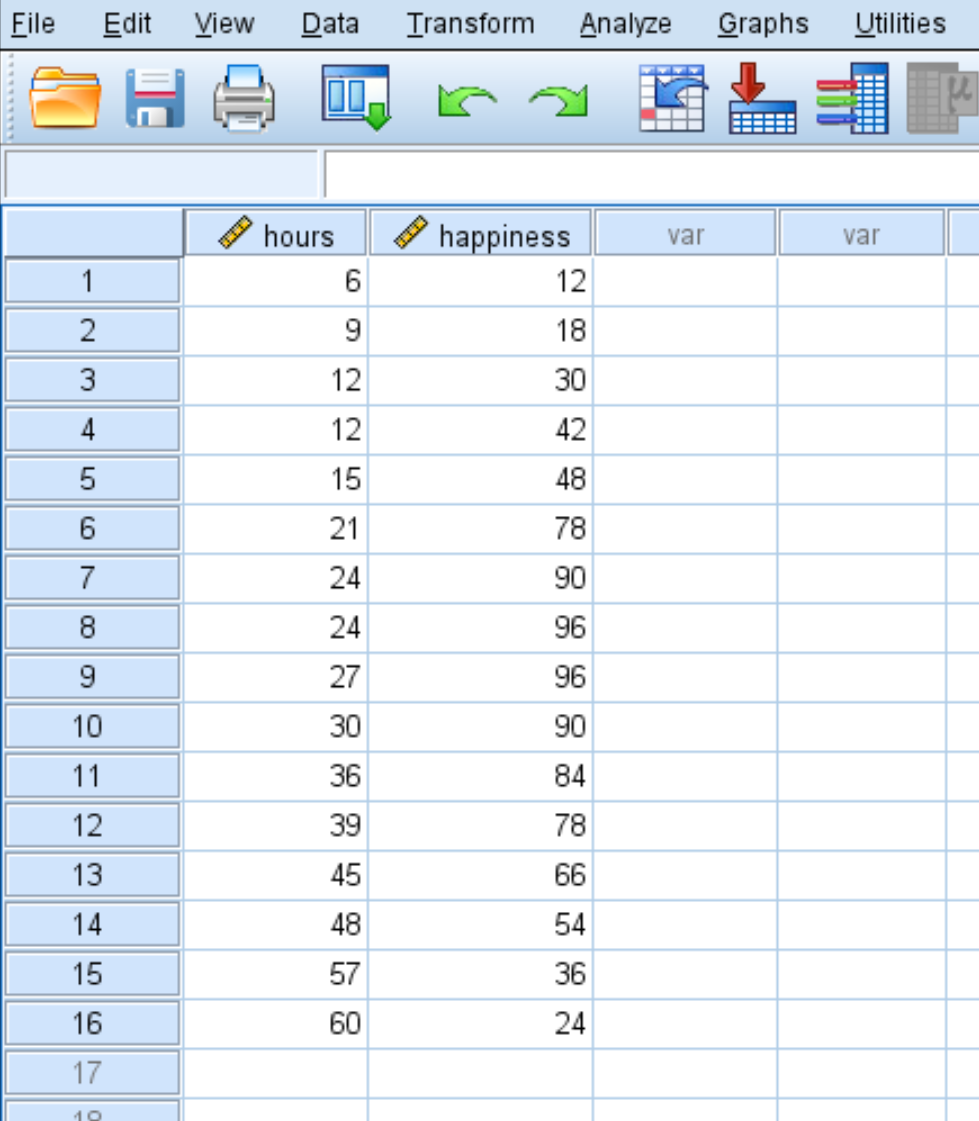
SPSS’de ikinci dereceden regresyon gerçekleştirmek için aşağıdaki adımları kullanın.

Adım 1: Verileri görselleştirin.

İkinci dereceden bir regresyon gerçekleştirmeden önce, iki değişkenin gerçekte ikinci dereceden bir ilişkiye sahip olduğunu doğrulamak amacıyla çalışılan saat ile mutluluk arasındaki ilişkiyi görselleştirmek için bir dağılım grafiği oluşturalım.

Grafikler sekmesini ve ardından Grafik Oluşturucu’yu tıklayın :

Açılan yeni pencerede, Seçim listesinden Dağılım/Nokta’yı seçin. Daha sonra Basit Dağılım etiketli grafiği ana düzenleme penceresine sürükleyin. Değişken saatleri x eksenine ve mutluluğu y eksenine sürükleyin. Daha sonra Tamam’ı tıklayın.

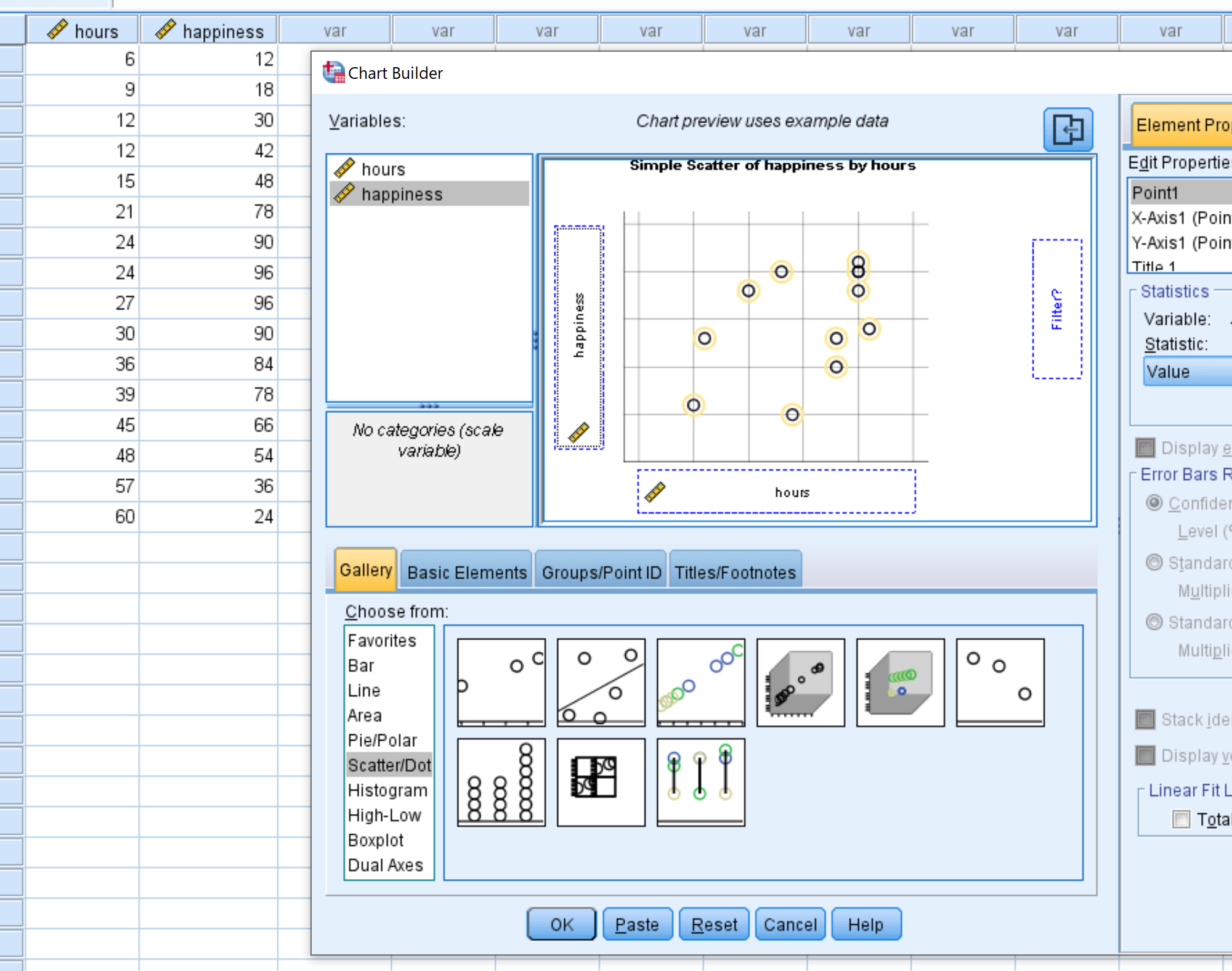
Aşağıdaki dağılım grafiği görünecektir:

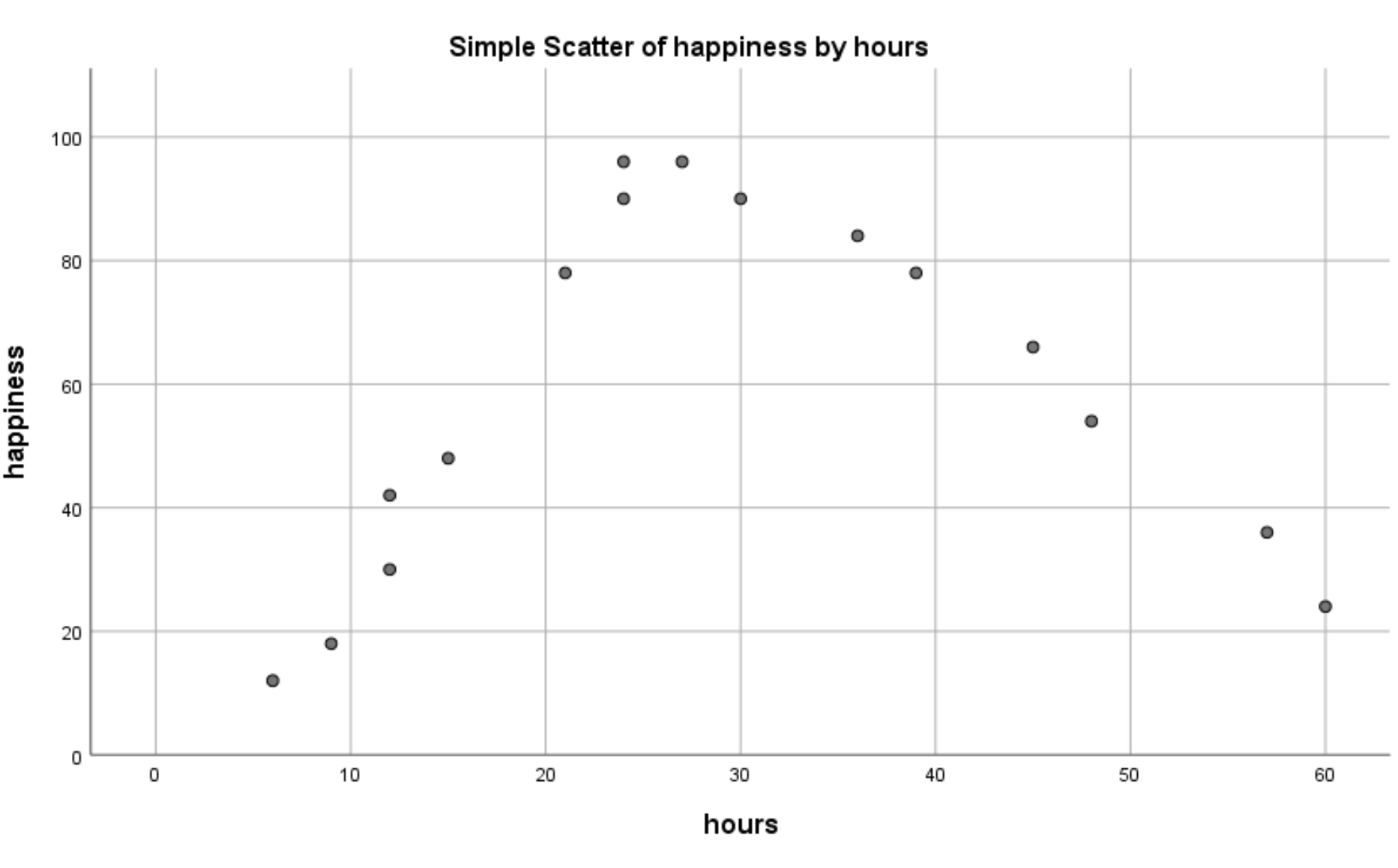
Çalışılan saat ile mutluluk arasında doğrusal olmayan bir ilişki olduğunu açıkça görebiliyoruz. Bu bize ikinci dereceden regresyonun bu durumda kullanmak için uygun bir teknik olduğunu söyler.

Adım 2: Yeni bir değişken oluşturun.

İkinci dereceden bir regresyon gerçekleştirmeden önce, saat ² için bir tahmin değişkeni oluşturmamız gerekir.

Dönüşüm sekmesini ve ardından Değişkeni Hesapla’yı tıklayın :

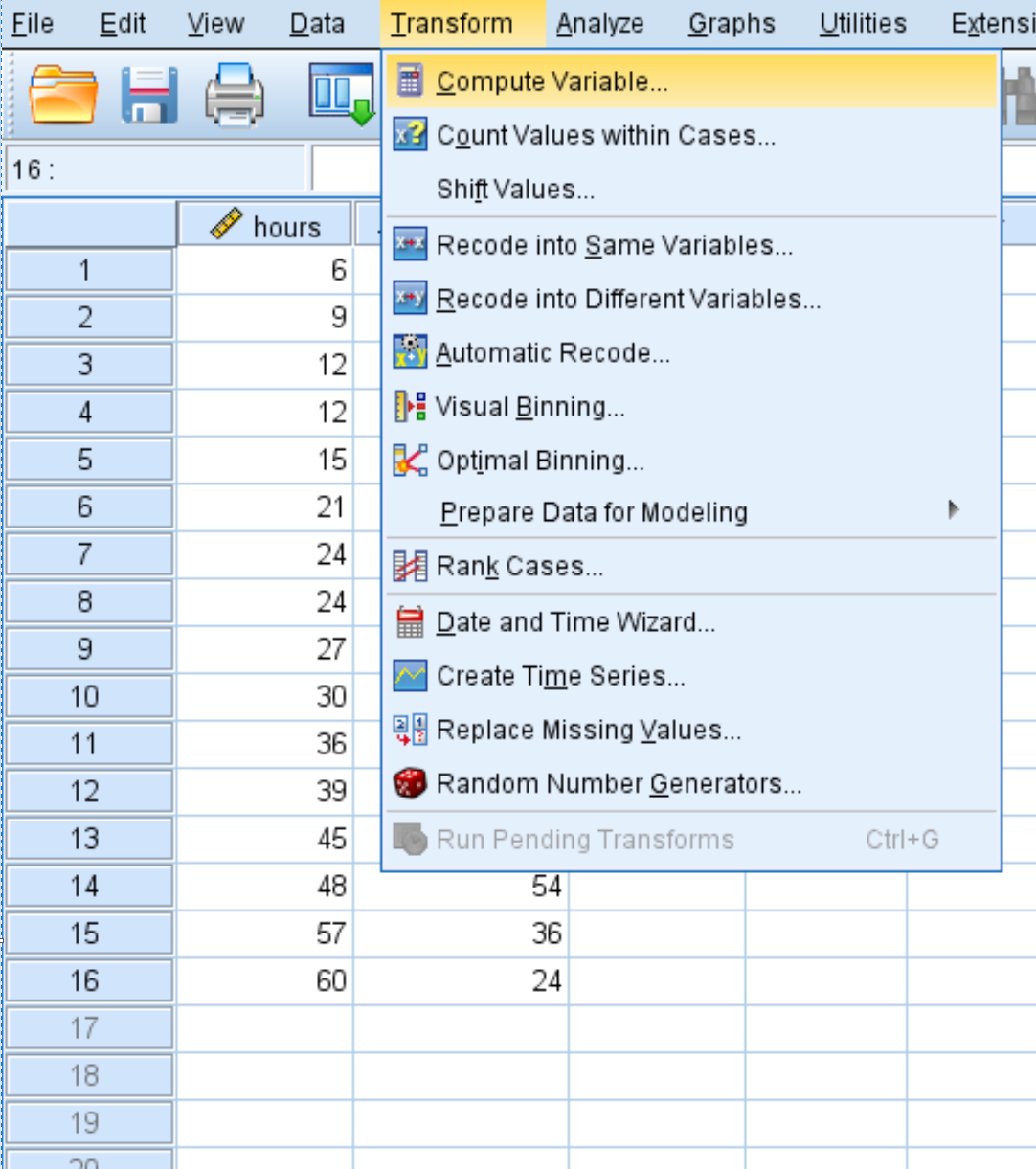
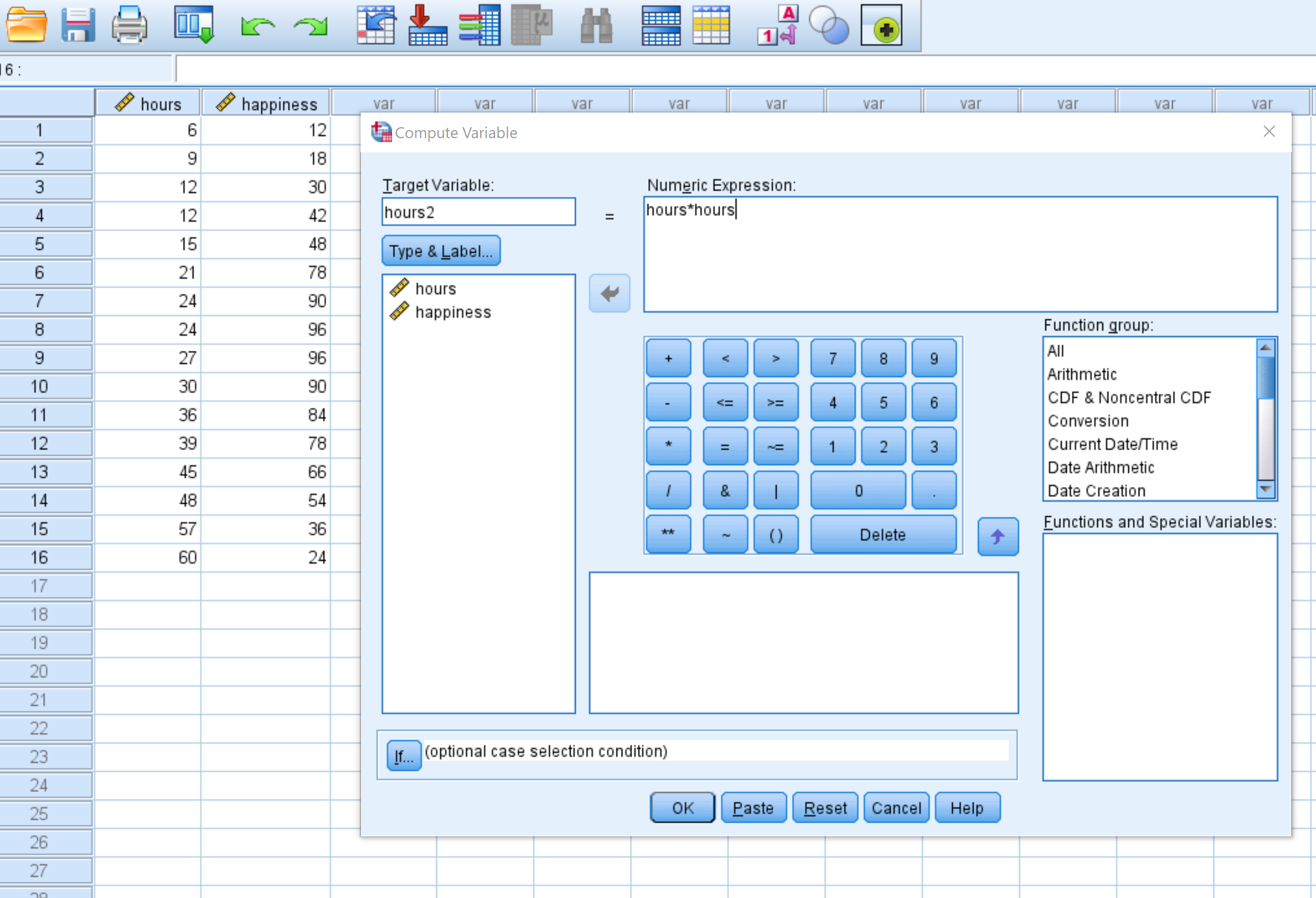
Görüntülenen yeni pencerede hedef değişkene saat2 adını verin ve onu saat*saat olarak ayarlayın:

Tamam’a tıkladığınızda, saat2 değişkeni yeni bir sütunda görünecektir:

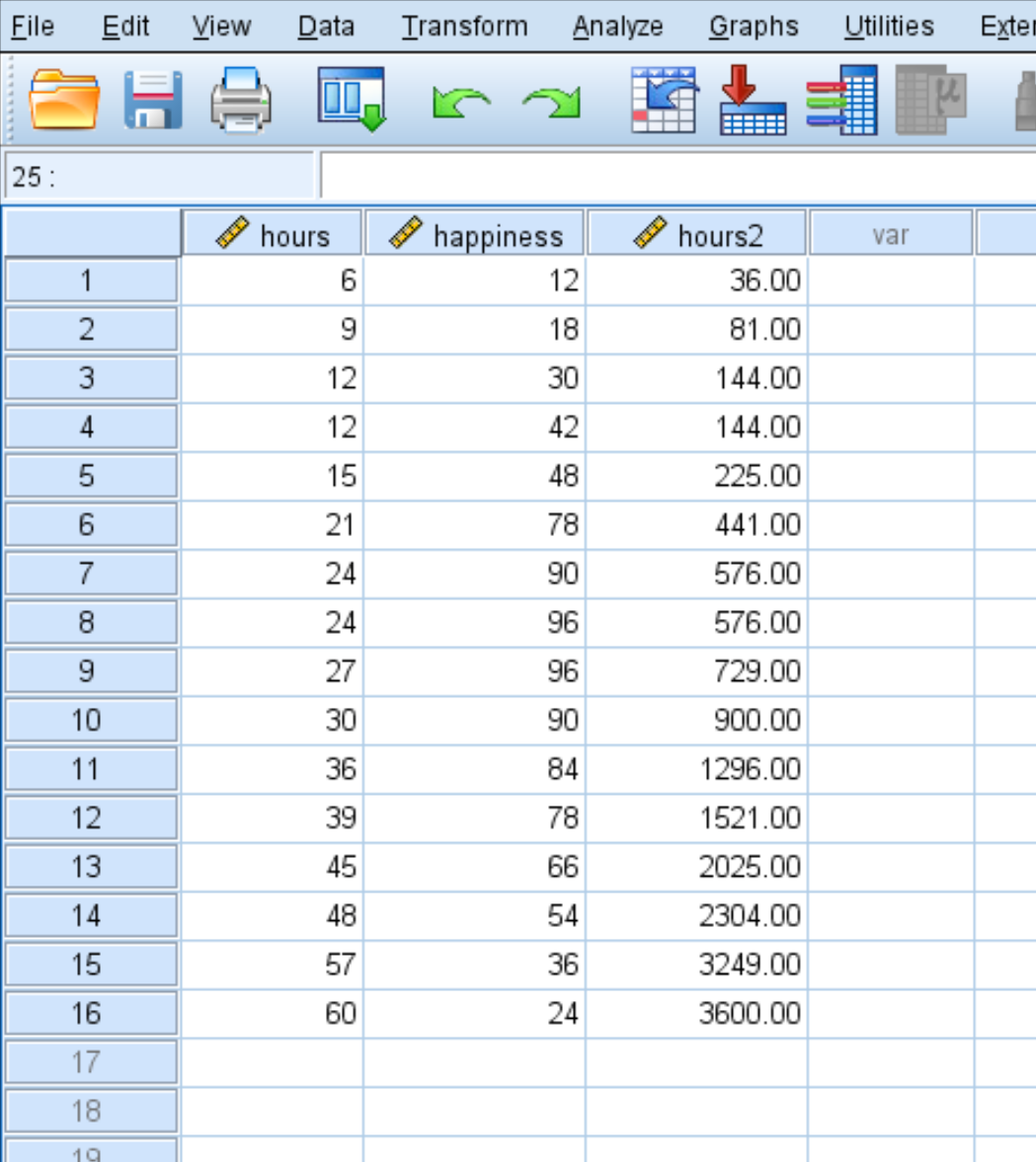
Adım 3: İkinci dereceden regresyon gerçekleştirin.

Daha sonra ikinci dereceden regresyon gerçekleştireceğiz. Analiz sekmesine, ardından Regresyon’a ve ardından Doğrusal’a tıklayın:

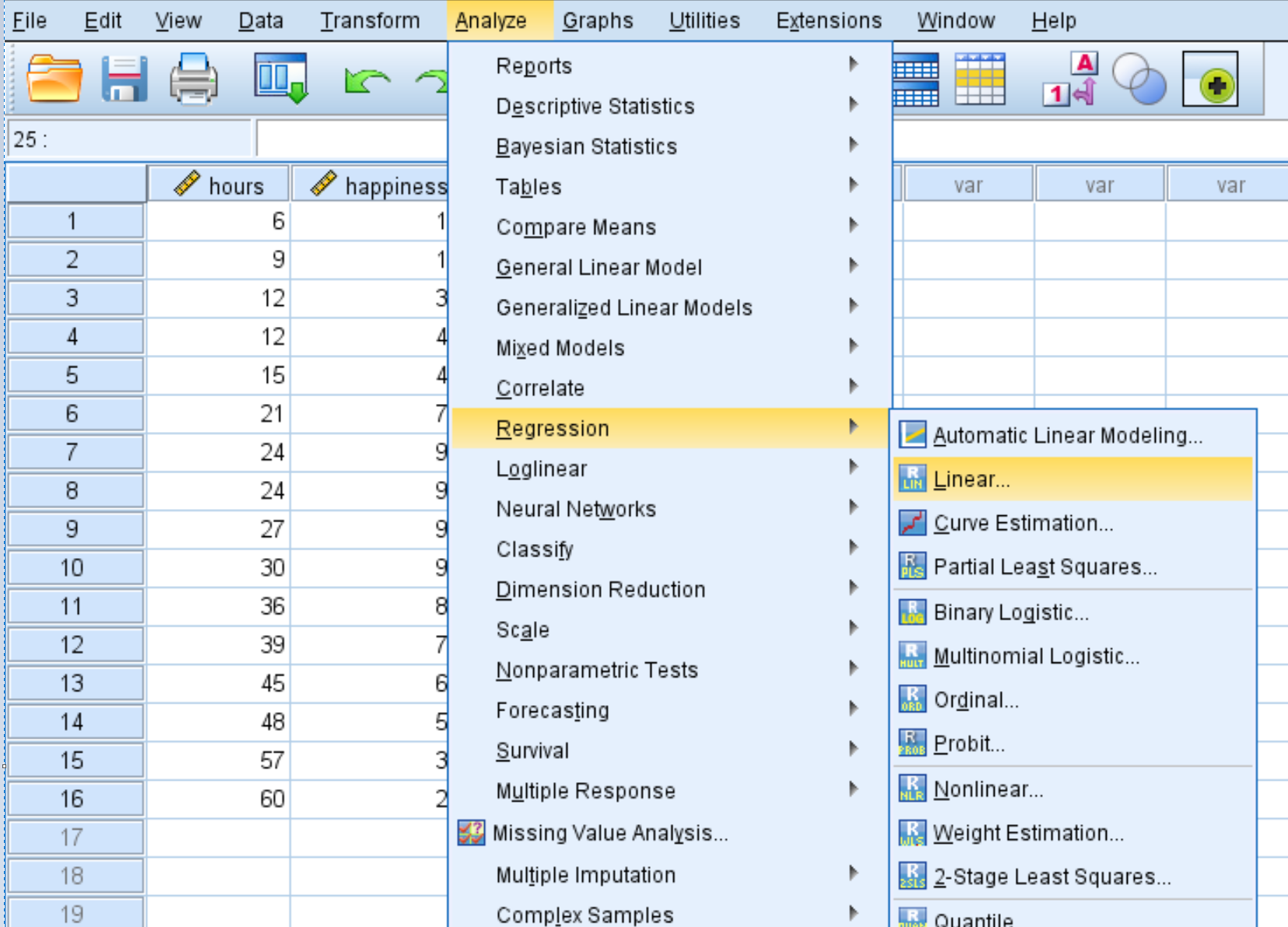
Açılan yeni pencerede mutluluğu Bağımlı etiketli kutuya sürükleyin. Hours ve Hours2’yi Bağımsız(lar) etiketli kutuya sürükleyin. Daha sonra Tamam’ı tıklayın.

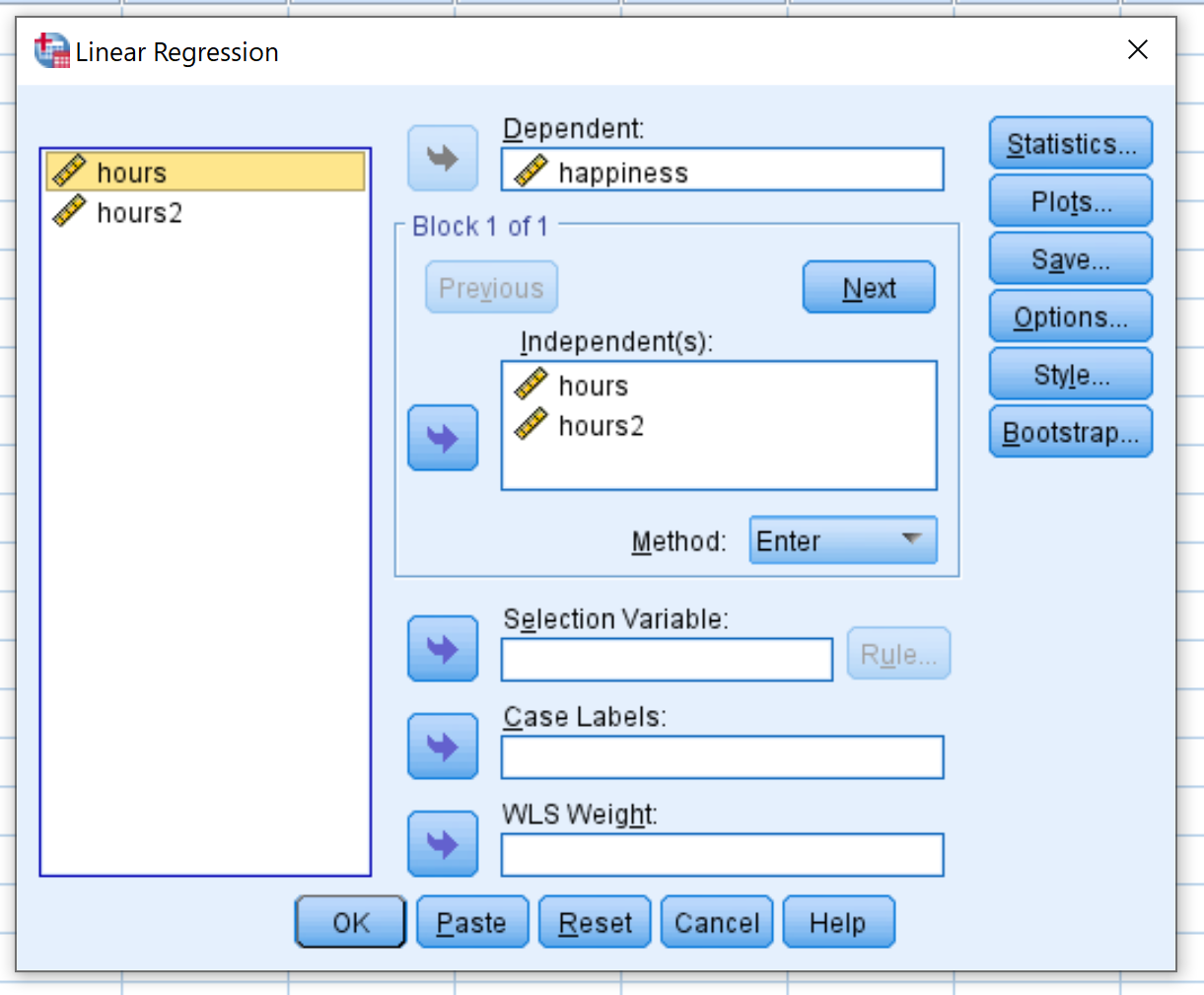
Adım 4: Sonuçları yorumlayın.

Tamam’a tıkladığınızda ikinci dereceden regresyon sonuçları yeni bir pencerede görünecektir.

Bizi ilgilendiren ilk tabloya Model Özeti adı verilir:

Bu tablodaki en alakalı sayıları nasıl yorumlayacağınız aşağıda açıklanmıştır:

• R Kare: Yanıt değişkenindeki açıklayıcı değişkenler tarafından açıklanabilen varyansın oranıdır. Bu örnekte mutluluktaki değişimin %90,9’u saat ve saat ² değişkeniyle açıklanabilmektedir.
• Standart. Tahmin hatası: Standart hata , gözlemlenen değerler ile regresyon çizgisi arasındaki ortalama mesafedir. Bu örnekte gözlemlenen değerler regresyon doğrusundan ortalama 9.519 birim sapmaktadır.

Bizi ilgilendiren bir sonraki tabloya ANOVA adı veriliyor:

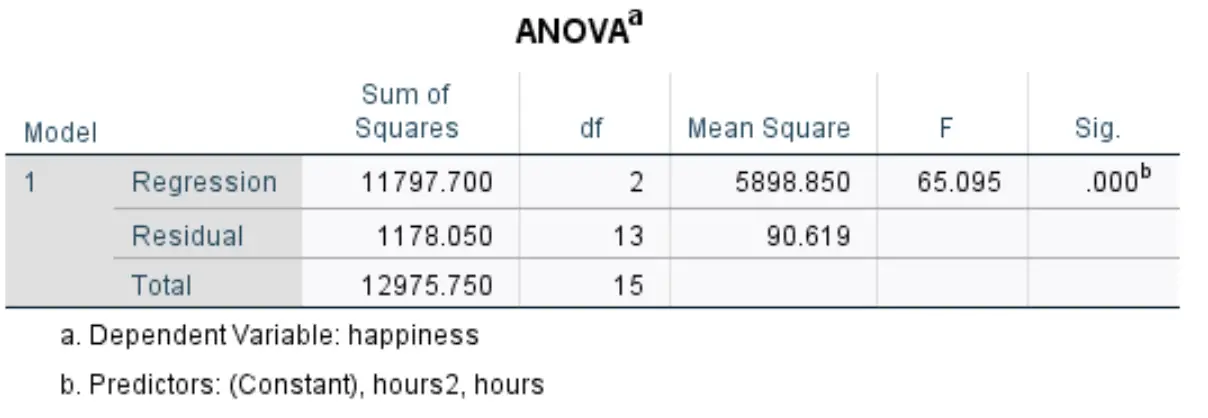
Bu tablodaki en alakalı sayıları nasıl yorumlayacağınız aşağıda açıklanmıştır:

• F: Bu, Regresyon modeli için Ortalama Kare Regresyon / Ortalama Kareler Artık olarak hesaplanan genel F istatistiğidir.
• Sig: Bu, genel F istatistiğiyle ilişkili p değeridir. Bu bize regresyon modelinin bir bütün olarak istatistiksel olarak anlamlı olup olmadığını söyler. Bu durumda p değeri 0,000’e eşittir; bu, açıklayıcı değişkenler saat ve saat ^2’nin birleşiminin sınav sonucuyla istatistiksel olarak anlamlı bir ilişkiye sahip olduğunu gösterir.

Bizi ilgilendiren aşağıdaki tablo Katsayılar başlığını taşımaktadır:

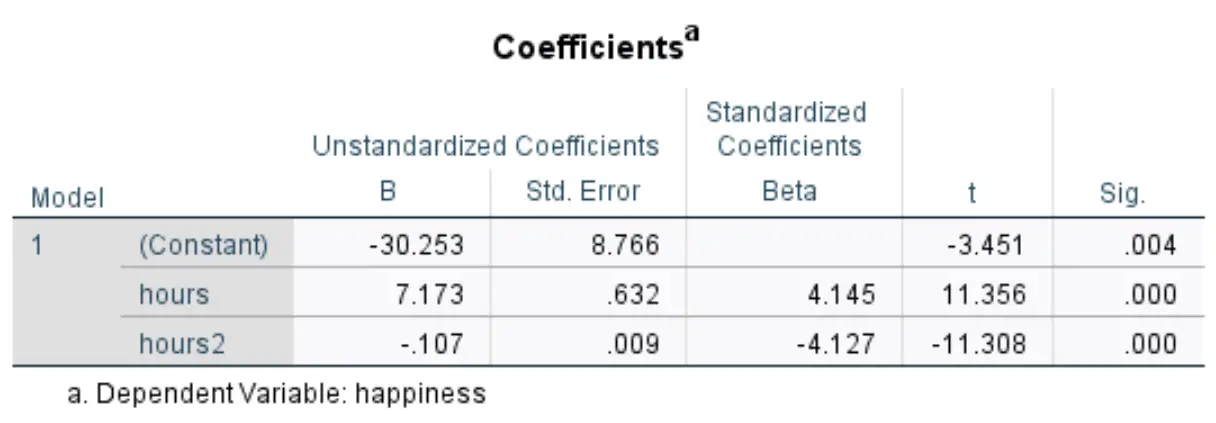
Bu veri seti için tahmini regresyon denklemini oluşturmak amacıyla Standartlaştırılmamış B sütunundaki değerleri kullanabiliriz:

Tahmini mutluluk düzeyi = -30,253 + 7,173*(saat) – 0,107*(saat ² )

Haftada çalışılan saat sayısına göre bireyin tahmini mutluluk düzeyini bulmak için bu denklemi kullanabiliriz. Örneğin haftada 60 saat çalışan bir kişinin mutluluk düzeyi 14,97 olmalıdır:

Tahmini mutluluk düzeyi = -30,253 + 7,173*(60) – 0,107*(60 ² ) = 14,97 .

Haftada 30 saat çalışan bir kişinin ise mutluluk düzeyinin 88,65 olması gerekiyor:

Tahmini mutluluk düzeyi = -30,253 + 7,173*(30) – 0,107*(30 ² ) = 88,65 .

Adım 5: Sonuçları rapor edin.

Son olarak ikinci dereceden regresyonumuzun sonuçlarını bildirmek istiyoruz. İşte bunun nasıl yapılacağına dair bir örnek:

Bir bireyin çalıştığı saat sayısı ile buna karşılık gelen mutluluk düzeyi (0’dan 100’e kadar ölçülür) arasındaki ilişkiyi ölçmek için ikinci dereceden bir regresyon uygulandı. Analizde 16 kişilik bir örneklem kullanıldı.

Sonuçlar açıklayıcı değişkenler saat ve saat ² ile yanıt değişkeni mutluluk arasında istatistiksel olarak anlamlı bir ilişki olduğunu gösterdi (F(2, 13) = 65.095, p < 0.000).

Bu iki açıklayıcı değişken birlikte mutluluktaki değişkenliğin %90,9’unu oluşturuyordu.

Regresyon denklemi şu şekilde ortaya çıktı:

Tahmini mutluluk düzeyi = -30,253 + 7,173 (saat) – 0,107 ( ² saat)