Spss'de roc eğrisi nasıl oluşturulur ve yorumlanır

Lojistik regresyon, yanıt değişkeni ikili olduğunda bir regresyon modeline uymak için kullandığımız istatistiksel bir yöntemdir. Lojistik regresyon modelinin bir veri kümesine ne kadar iyi uyduğunu değerlendirmek için aşağıdaki iki ölçüme bakabiliriz:

• Duyarlılık: Sonuç gerçekten olumluyken modelin bir gözlem için olumlu bir sonuç tahmin etme olasılığı.
• Özgüllük: Sonuç gerçekten negatif olduğunda modelin bir gözlem için negatif bir sonuç öngörme olasılığı.

Bu iki ölçümü görselleştirmenin basit bir yolu, lojistik regresyon modelinin duyarlılığını ve özgüllüğünü gösteren bir grafik olan ROC eğrisi oluşturmaktır.

Bu eğitimde SPSS’de bir ROC eğrisinin nasıl oluşturulacağı ve yorumlanacağı açıklanmaktadır.

Örnek: SPSS’deki ROC eğrisi

Diyelim ki bir basketbolcunun NBA’e seçilip seçilmediğini (0 = hayır, 1 = evet) ve üniversitede maç başına aldığı puanı gösteren aşağıdaki veri setine sahibiz:

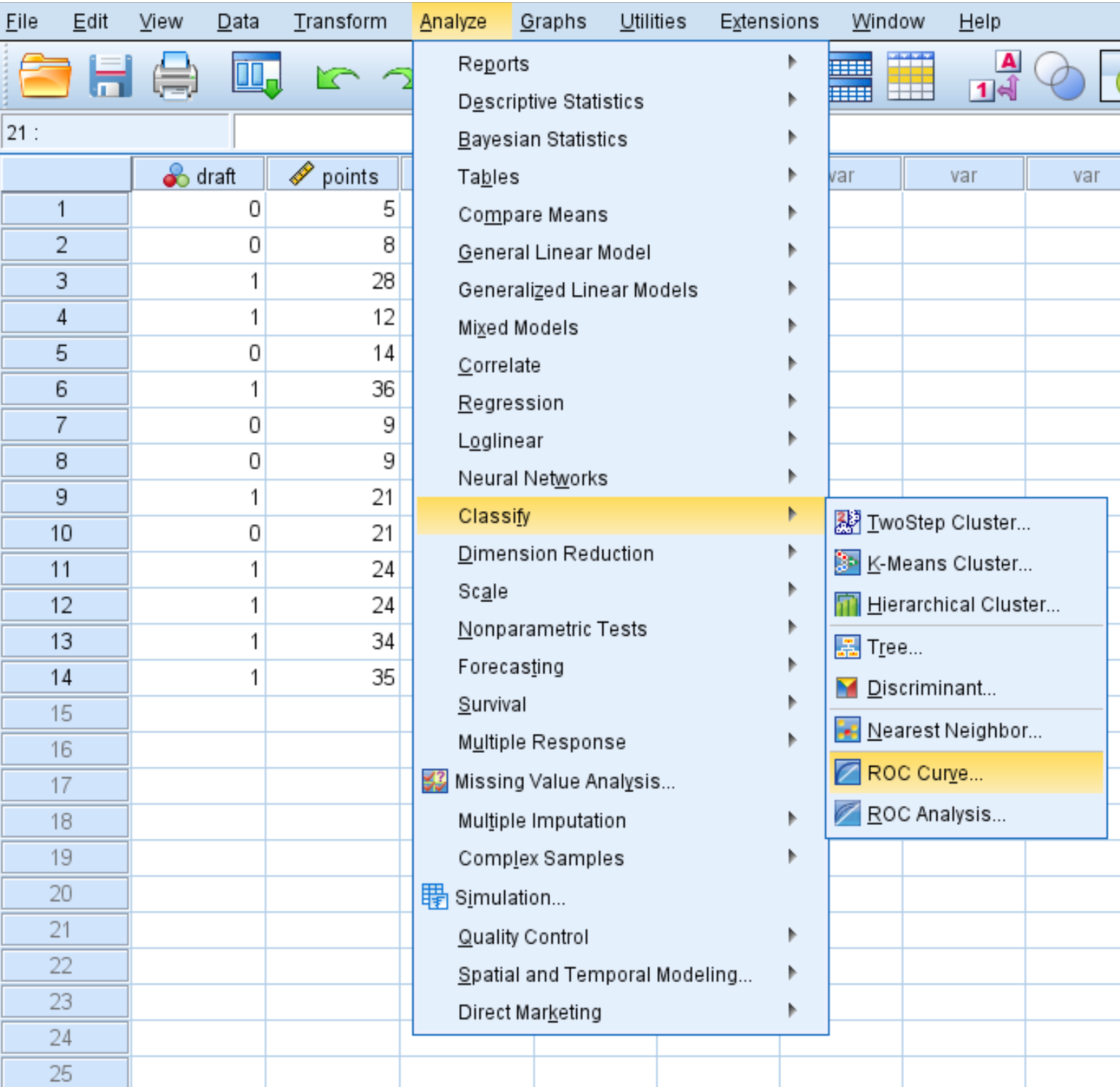
Bu veri kümesi için bir ROC eğrisi oluşturmak üzere Analiz Et sekmesine, ardından Sınıflandır’a ve ardından ROC Eğrisi’ne tıklayın:

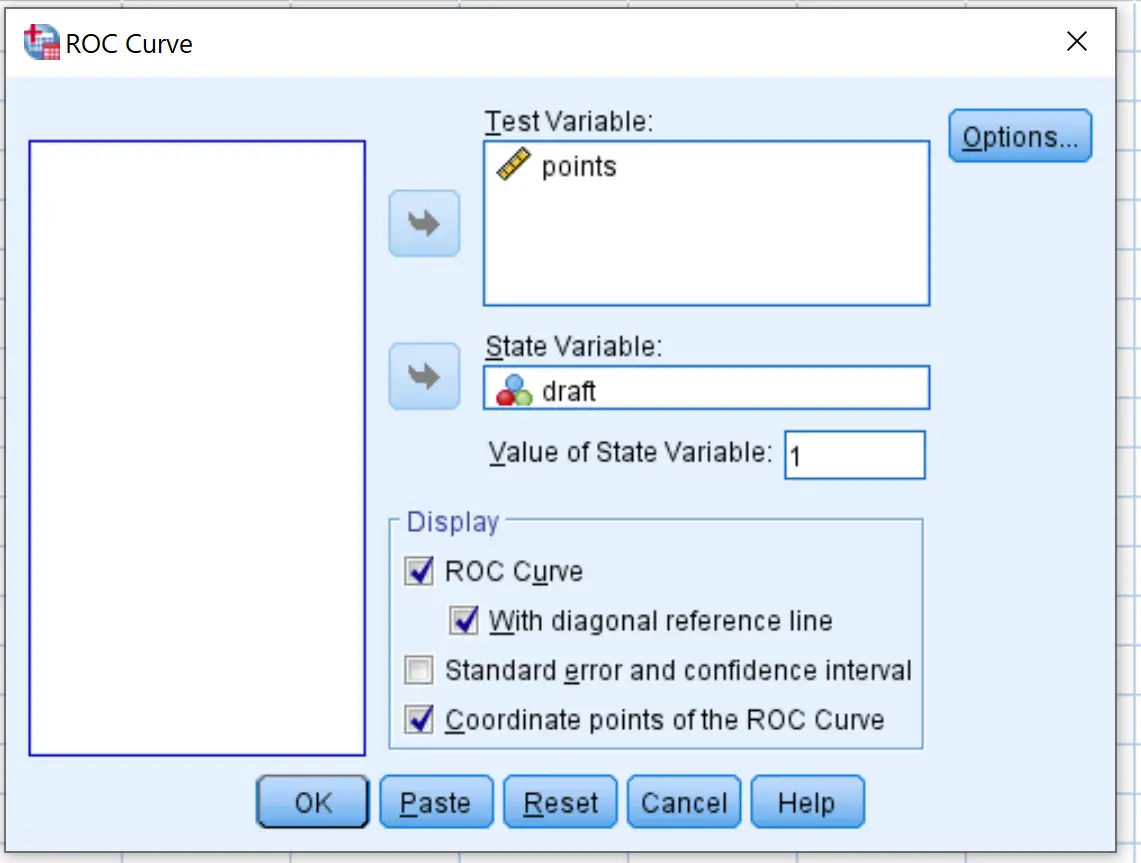
Açılan yeni pencerede taslak değişkenini Durum Değişkeni etiketli alana sürükleyin. Durum değişkeninin değerini 1 olarak ayarlayın. (Bu, bir oyuncunun draft edildiğini gösteren değerdir). Değişken noktalarını Test Değişkeni etiketli alana sürükleyin.

Çapraz referans çizgisi ve ROC eğrisi noktası koordinatları ile seçeneğinin yanındaki kutuları işaretleyin. Daha sonra Tamam’ı tıklayın.

Sonucun nasıl yorumlanacağı aşağıda açıklanmıştır:

Dosya işlemenin özeti:

Bu tablo veri kümesindeki pozitif ve negatif vakaların toplam sayısını gösterir. Bu örnekte, 8 oyuncu draft edildi (olumlu sonuç) ve 6 oyuncu draft edilmedi (negatif sonuç):

ROC eğrisi:

Alıcı Çalışma Karakteristiği (ROC) eğrisi, eşik değeri 0’dan 1’e değiştikçe duyarlılık değerlerinin özgüllük 1’e karşı grafiğidir:

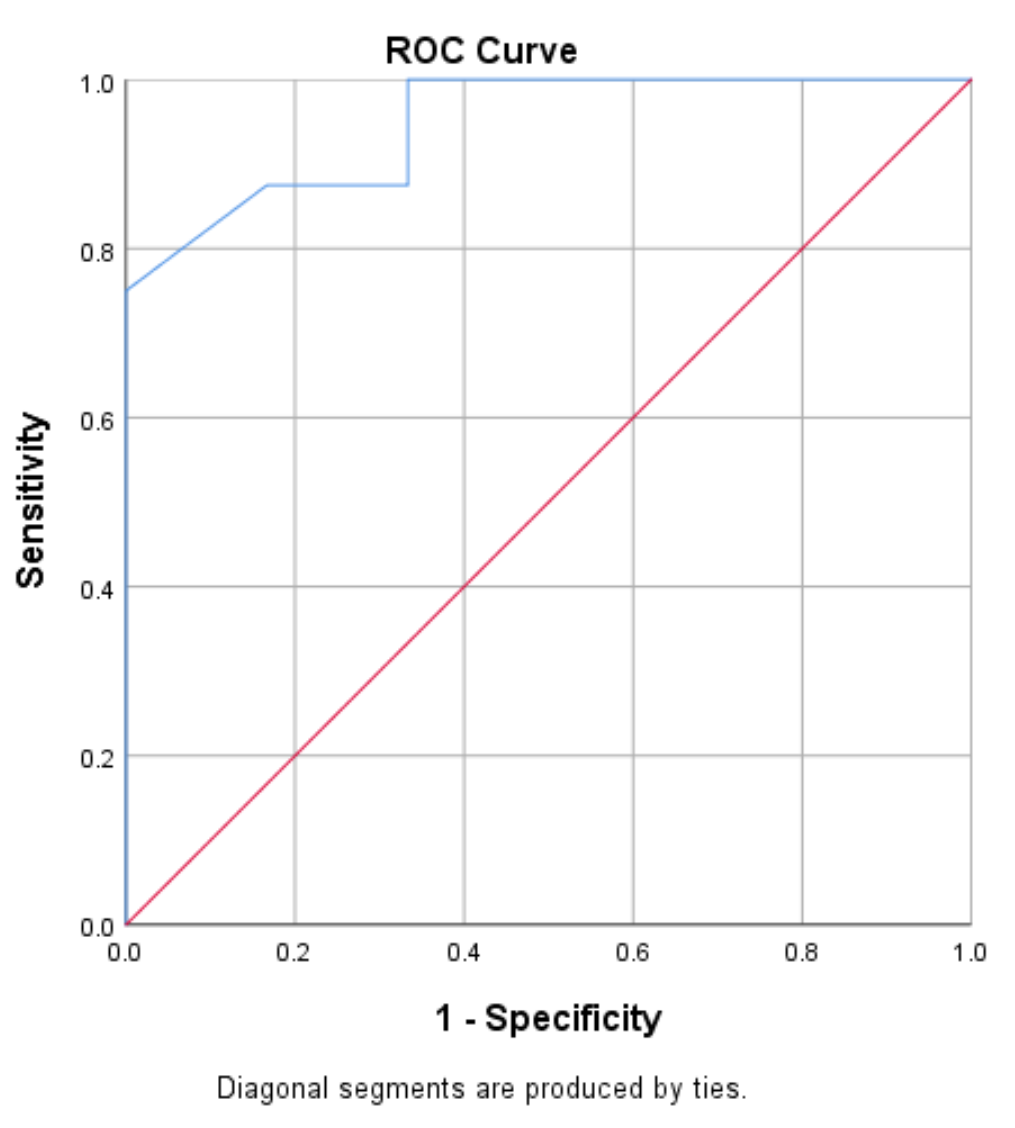
Duyarlılığı ve özgüllüğü yüksek olan bir model, grafiğin sol üst köşesine uyan bir ROC eğrisine sahip olacaktır. Duyarlılığı ve özgüllüğü düşük olan bir model, 45 derecelik diyagonale yakın bir eğriye sahip olacaktır.

Bu örnekteki ROC eğrisinin (mavi çizgi) grafiğin sol üst köşesini sardığını görebiliriz; bu da modelin, oyuncuların maç başına ortalama puanlarına dayalı olarak oyuncuların draft edilip edilmeyeceğini tahmin etme konusunda iyi bir iş çıkardığını gösterir. . .

Eğrinin altındaki alan:

Eğrinin altındaki alan bize modelin olumlu ve olumsuz sonuçları ayırt etme yeteneği hakkında fikir verir. AUC, 0 ile 1 arasında değişebilir. AUC ne kadar yüksek olursa, model sonuçları doğru şekilde sınıflandırmada o kadar iyi olur.

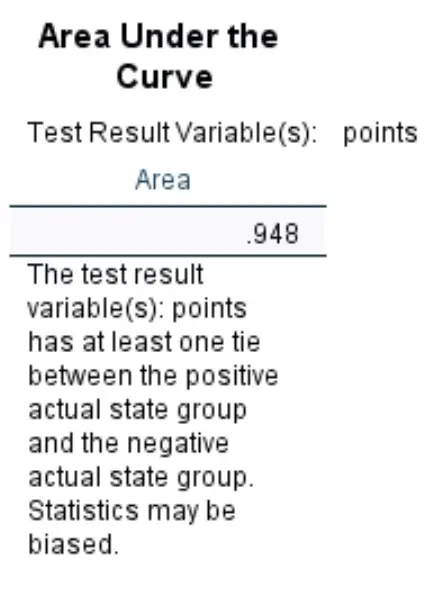
Bu özel lojistik regresyon modeli için AUC’nin son derece yüksek olan 0,948 olduğunu görebiliriz. Bu, modelin bir oyuncunun draft edilip edilmeyeceğini tahmin etme konusunda iyi bir iş çıkardığını gösteriyor.

Eğrinin koordinatları:

Bu son tablo, farklı eşikler için ROC eğrisinin duyarlılığını ve özgüllüğünü 1 gösterir.

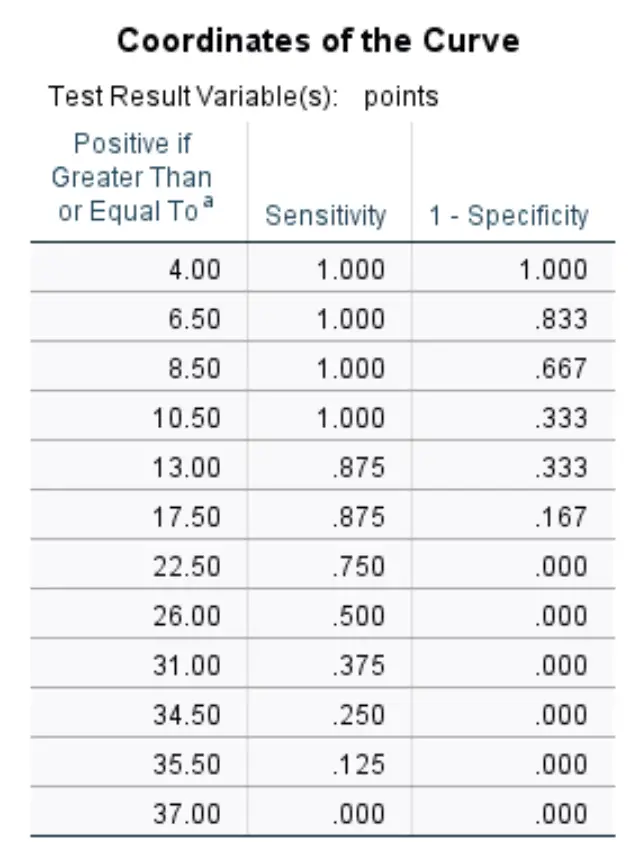
Örneğin:

Eşiğin 8,50 olmasına izin verirsek, bu, maç başına 8,50 puanın altında puan alan herhangi bir oyuncunun draft edilmeyeceğini ve maç başına 8,50 puanın üzerinde puan alan herhangi bir oyuncunun draft edileceği anlamına gelir.

Bunu bir eşik olarak kullanırsak, hassasiyetimiz %100 olacaktır (maç başına 8,50 sayıdan daha az puan alan her oyuncu gerçekten draft edilmediğinden) ve özgüllüğümüz 1 %66,7 olacaktır (12 oyuncudan 8,50 puandan daha fazla puan alan 8 oyuncu olduğundan) oyun başına draft edildi).

Yukarıdaki tablo, her potansiyel eşik için duyarlılık ve özgüllüğü 1 görmemizi sağlar.