Spss'de kovaryans matrisi nasıl oluşturulur

Kovaryans , bir değişkendeki değişikliklerin ikinci bir değişkendeki değişikliklerle nasıl ilişkilendirildiğinin bir ölçüsüdür. Daha spesifik olarak, iki değişkenin doğrusal olarak ilişkili olma derecesinin bir ölçüsüdür.

İki değişken ( X ve Y) arasındaki kovaryansı hesaplamak için kullanılan formül:

COV( X , Y ) = Σ(x- x )(y- y ) / n

Kovaryans matrisi, bir veri kümesindeki farklı değişkenler arasındaki kovaryansı gösteren bir kare matristir.

Bu eğitimde SPSS’de belirli bir veri seti için kovaryans matrisinin nasıl oluşturulacağı açıklanmaktadır.

Örnek: SPSS’deki Kovaryans matrisi

10 farklı öğrencinin üç dersteki (matematik, fen bilimleri ve tarih) test puanlarını gösteren aşağıdaki veri setine sahip olduğumuzu varsayalım:

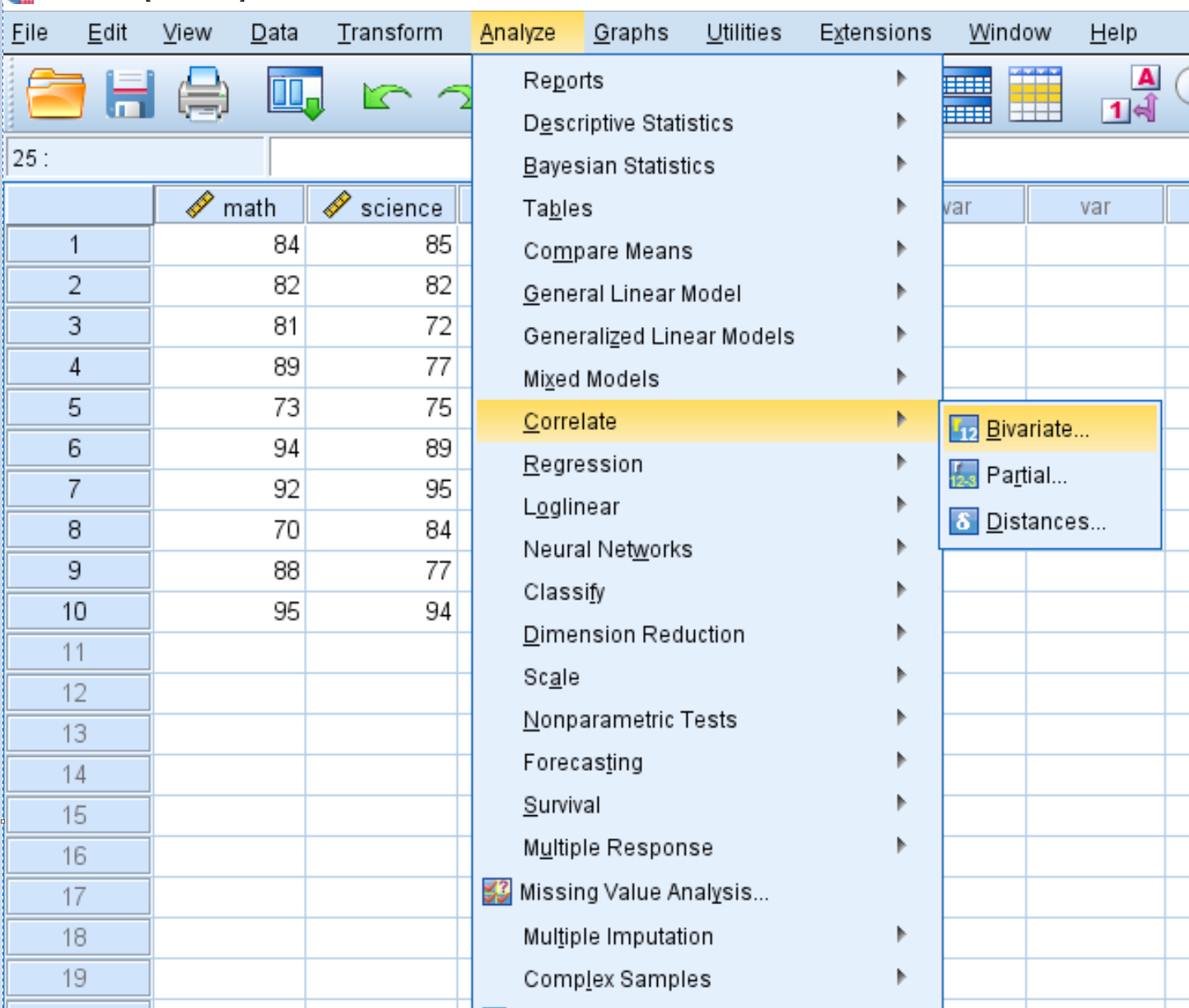
Bu veri kümesi için bir kovaryans matrisi oluşturmak için Analiz Et sekmesine, ardından Korele Et’e ve ardından İki Değişkenli’ye tıklayın:

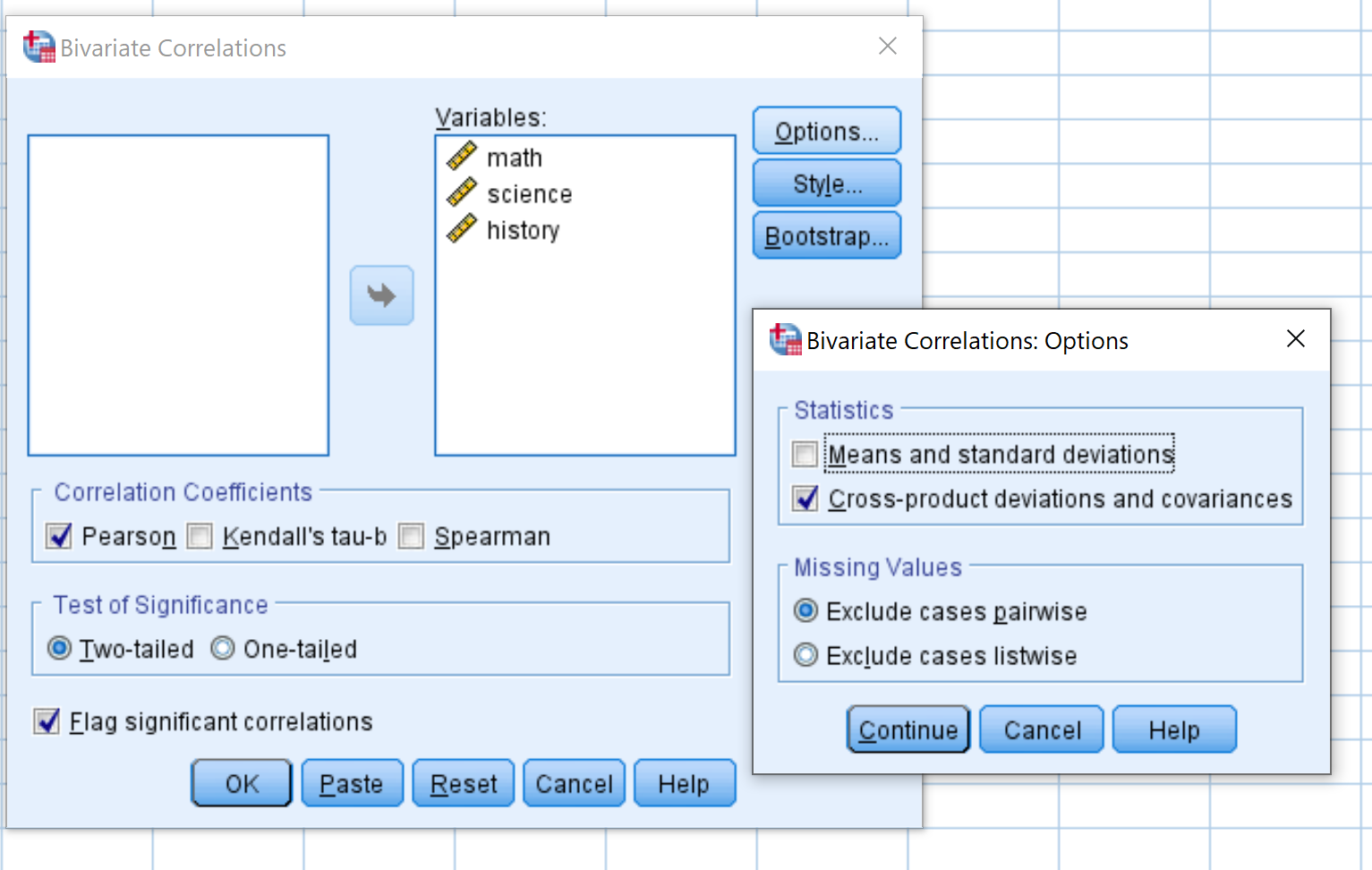
Açılan yeni pencerede, üç değişkenin her birini Değişkenler etiketli kutuya sürükleyin:

Ardından Seçenekler’i tıklayın. Ürünler arasındaki farklar ve kovaryanslar’ın yanındaki kutuyu işaretleyin. Daha sonra Devam’ı tıklayın.

Daha sonra Tamam’ı tıklayın. Sonuç yeni bir pencerede görünecektir:

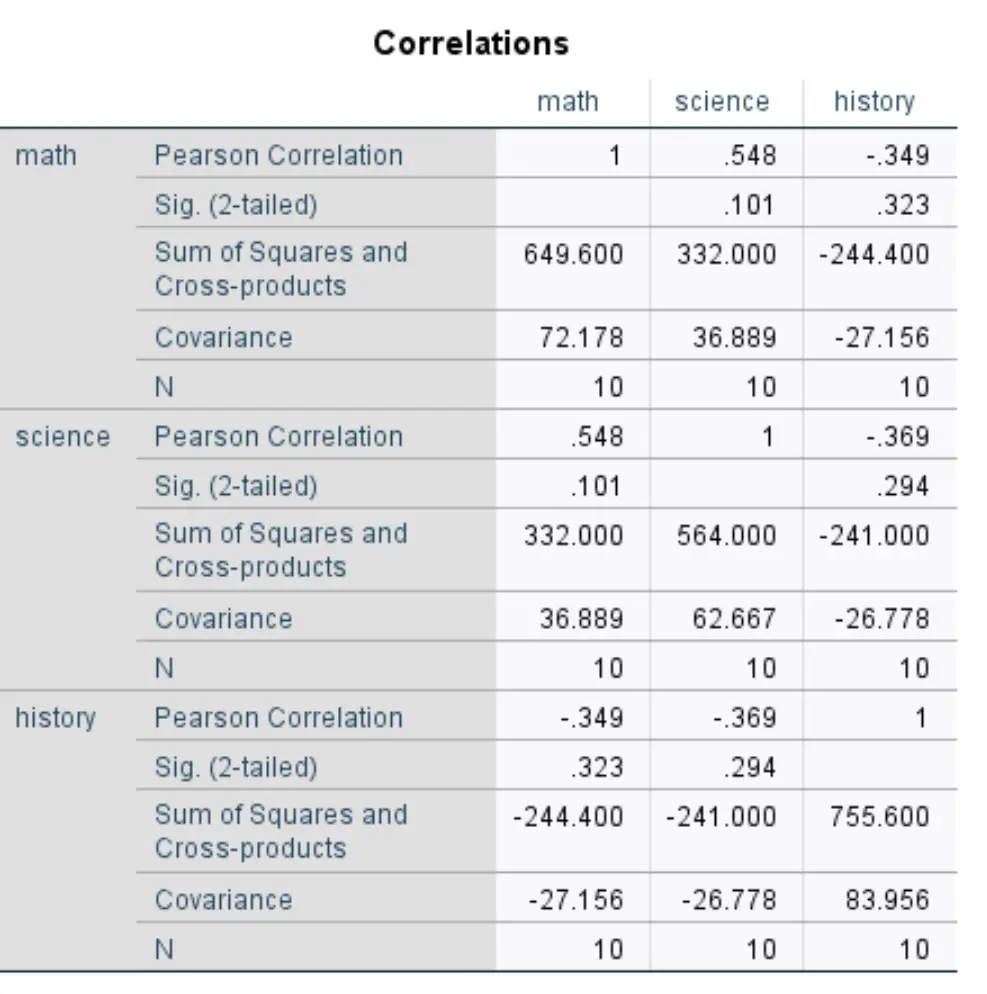
Değişkenlerin her ikili kombinasyonunun kovaryansını elde etmek için, kareler ve vektör çarpımlarının toplamını N’ye bölmeniz gerekir.

Örneğin matematik ve fen bilimleri arasındaki kovaryans şu şekilde hesaplanabilir:

COV (matematik, fen bilimleri) = 332.000 / 10 = 33,2 .

Benzer şekilde matematik ile tarih arasındaki kovaryans da şu şekilde hesaplanabilir:

COV (matematik, tarih) = -244,400 / 10 = -24,44 .

Ayrıca her değişkenin varyansını , karelerin ve vektör çarpımlarının toplamını N’ye bölerek de elde edebilirsiniz.

Örneğin matematikteki varyans şu şekilde hesaplanabilir:

VAR(matematik) = 649,600 / 10 = 64,96 .

Benzer hesaplamaları yaparak bu veri seti için tam kovaryans matrisini elde edebilirsiniz:

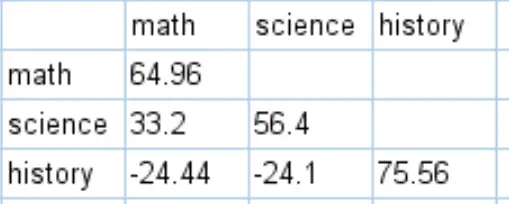
Kovaryans matrisi nasıl yorumlanır?

Kovaryans matrisinin köşegenleri boyunca yer alan değerler, her bir konunun varyanslarıdır. Örneğin:

• Matematik sonuçlarının varyansı 64,96’dır .
• Fen bilimleri puanlarının varyansı 56,4’tür .
• Tarihsel puanların varyansı 75,56’dır .

Matrisin diğer değerleri farklı konular arasındaki kovaryansları temsil eder. Örneğin:

• Matematik ve fen bilimleri puanları arasındaki kovaryans 33,2’dir .
• Matematik ve tarih puanları arasındaki kovaryans -24,44’tür .
• Fen ve tarih puanları arasındaki kovaryans -24,1’dir .

Kovaryans için pozitif bir sayı, iki değişkenin art arda artma veya azalma eğiliminde olduğunu gösterir. Örneğin matematik ve fen bilimleri arasında pozitif bir kovaryans (33.2) vardır; bu da matematikte yüksek puan alan öğrencilerin fen bilimlerinde de yüksek puan alma eğiliminde olduğunu gösterir. Benzer şekilde matematikte zayıf performans gösteren öğrenciler fen alanında da düşük performans gösterme eğilimindedir.

Kovaryans için negatif bir sayı, bir değişken artarken ikinci bir değişkenin azalma eğiliminde olduğunu gösterir. Örneğin, bilim ve tarihin negatif bir kovaryansı (-24,1) vardır, bu da fen bilimlerinde yüksek puan alan öğrencilerin tarihte düşük puan alma eğiliminde olduğunu gösterir. Benzer şekilde fen bilimlerinde düşük puan alan öğrenciler tarihte de yüksek puan alma eğilimindedir.

Ek kaynaklar

SPSS’de Korelasyon Matrisi Nasıl Oluşturulur
SPSS’de kısmi korelasyon nasıl hesaplanır