Spss'de lojistik regresyon nasıl yapılır

Lojistik regresyon, yanıt değişkeni ikili olduğunda bir regresyon modeline uymak için kullandığımız bir yöntemdir.

Bu eğitimde SPSS’de lojistik regresyonun nasıl gerçekleştirileceği açıklanmaktadır.

Örnek: SPSS’de lojistik regresyon

Kolej basketbol oyuncularının genel not ortalamalarına göre NBA’e alınıp alınmadığını (taslak: 0 = hayır, 1 = evet) gösteren bir veri seti için SPSS’de lojistik regresyon gerçekleştirmek üzere aşağıdaki adımları kullanın. oyun başına puanlar ve lig seviyeleri.

Adım 1: Verileri girin.

Öncelikle aşağıdaki verileri girin:

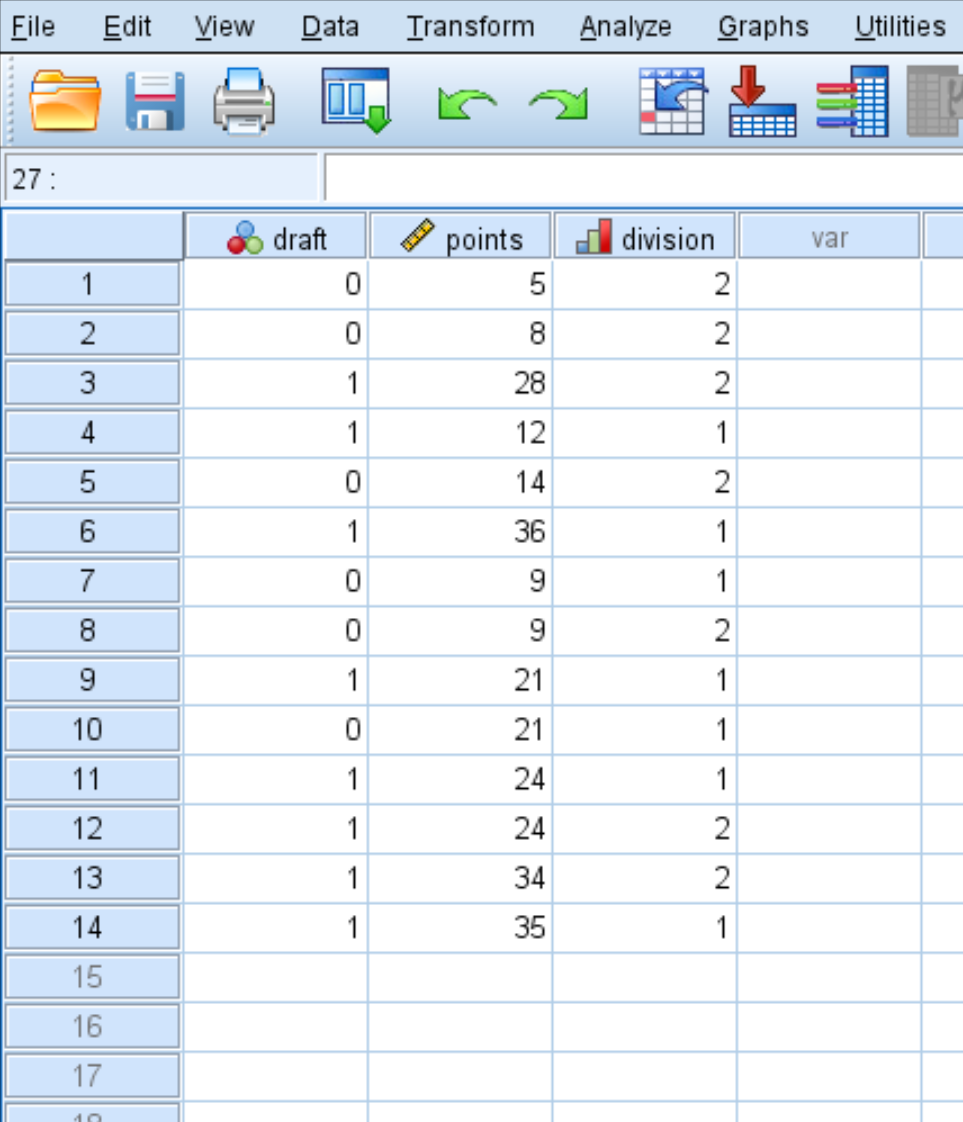
Adım 2: Lojistik regresyon gerçekleştirin.

Analiz sekmesine, ardından Regresyon’a ve ardından İkili Lojistik Regresyon’a tıklayın:

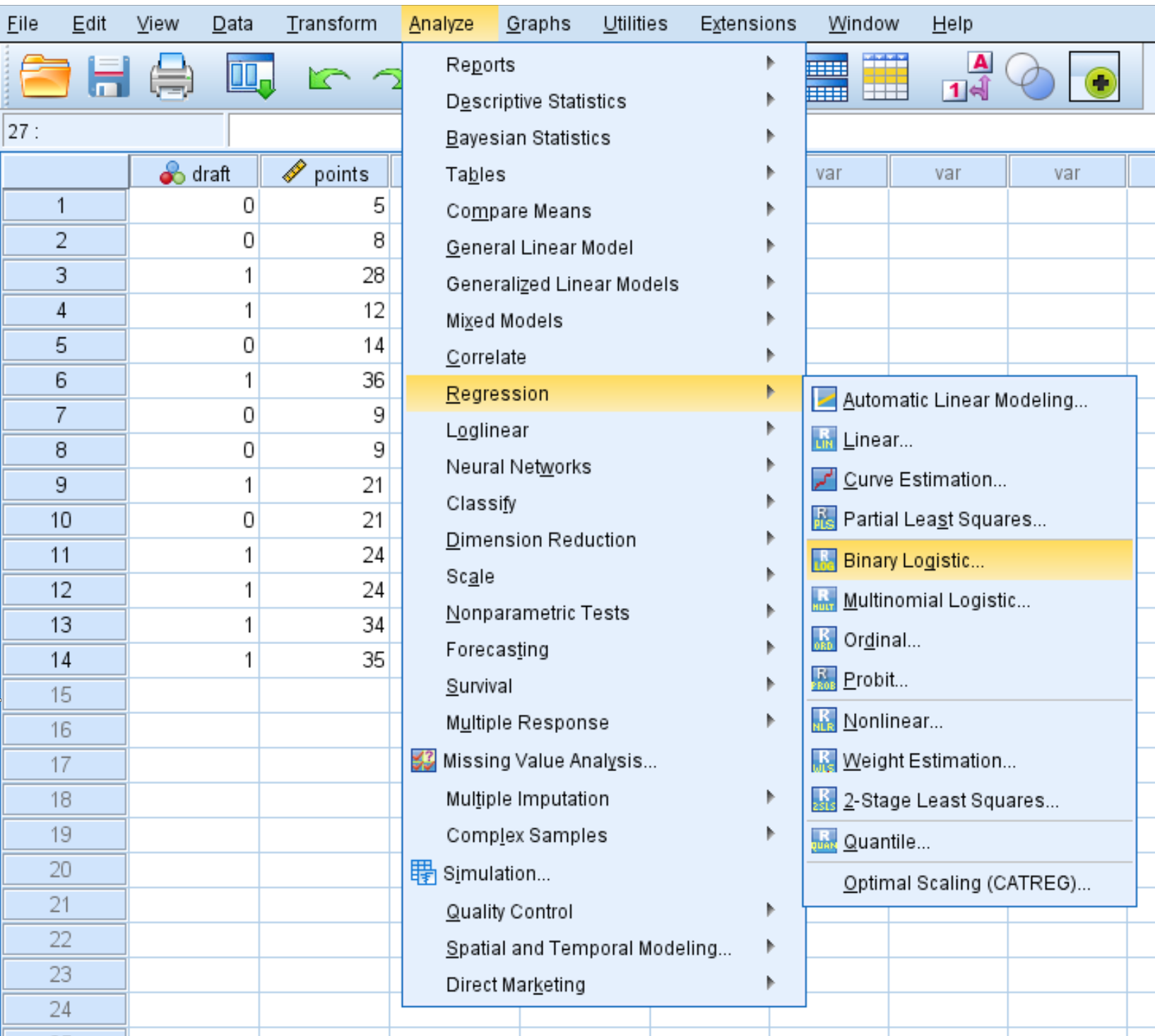
Açılan yeni pencerede ikili yanıt değişkeni projesini Bağımlı etiketli alana sürükleyin. Daha sonra tahmin değişkenlerinin iki nokta üst üste işaretini ve bölümünü Blok 1 / 1 etiketli kutuya sürükleyin. Yöntemi Enter’a ayarlanmış halde bırakın. Daha sonra Tamam’ı tıklayın.

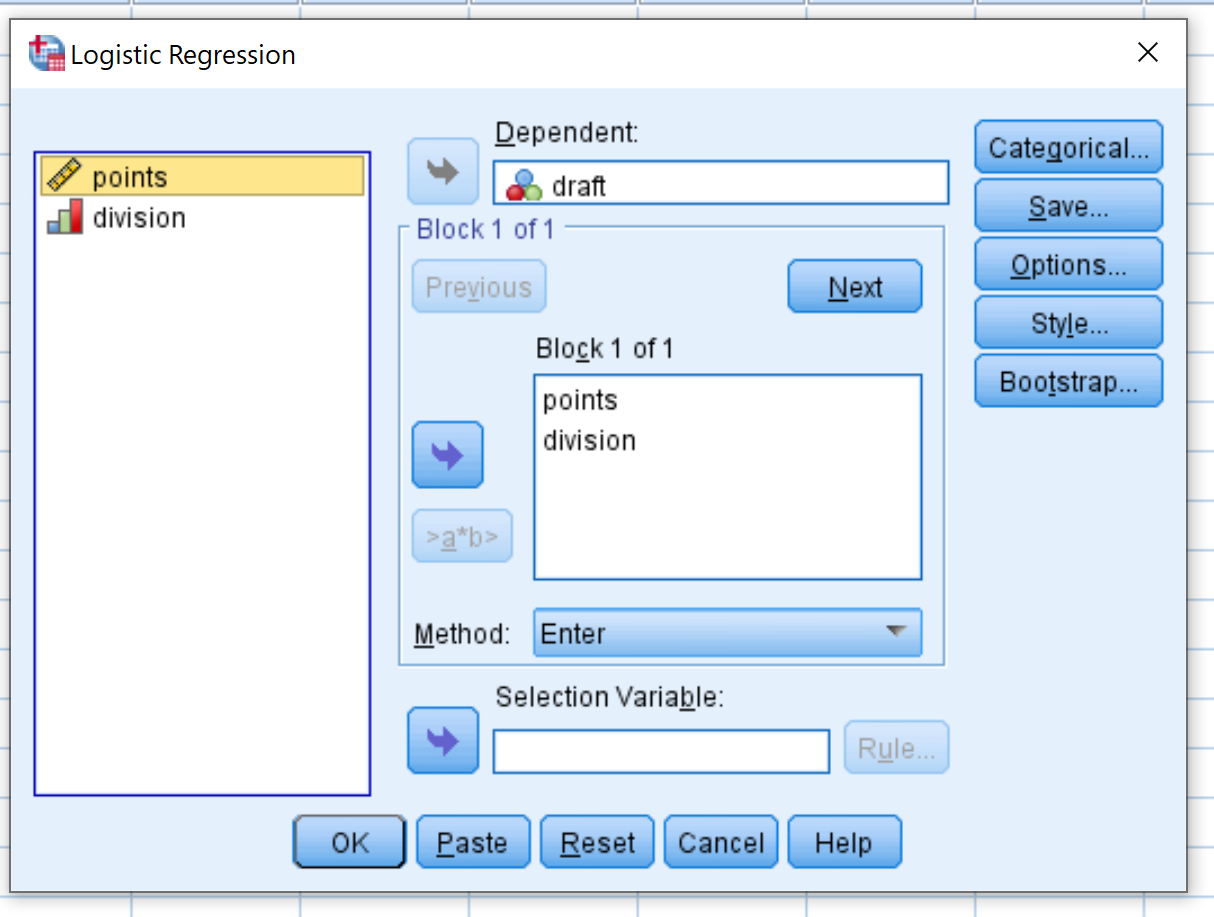
Adım 3. Sonucu yorumlayın.

Tamam’a tıkladığınızda lojistik regresyon sonucu görünecektir:

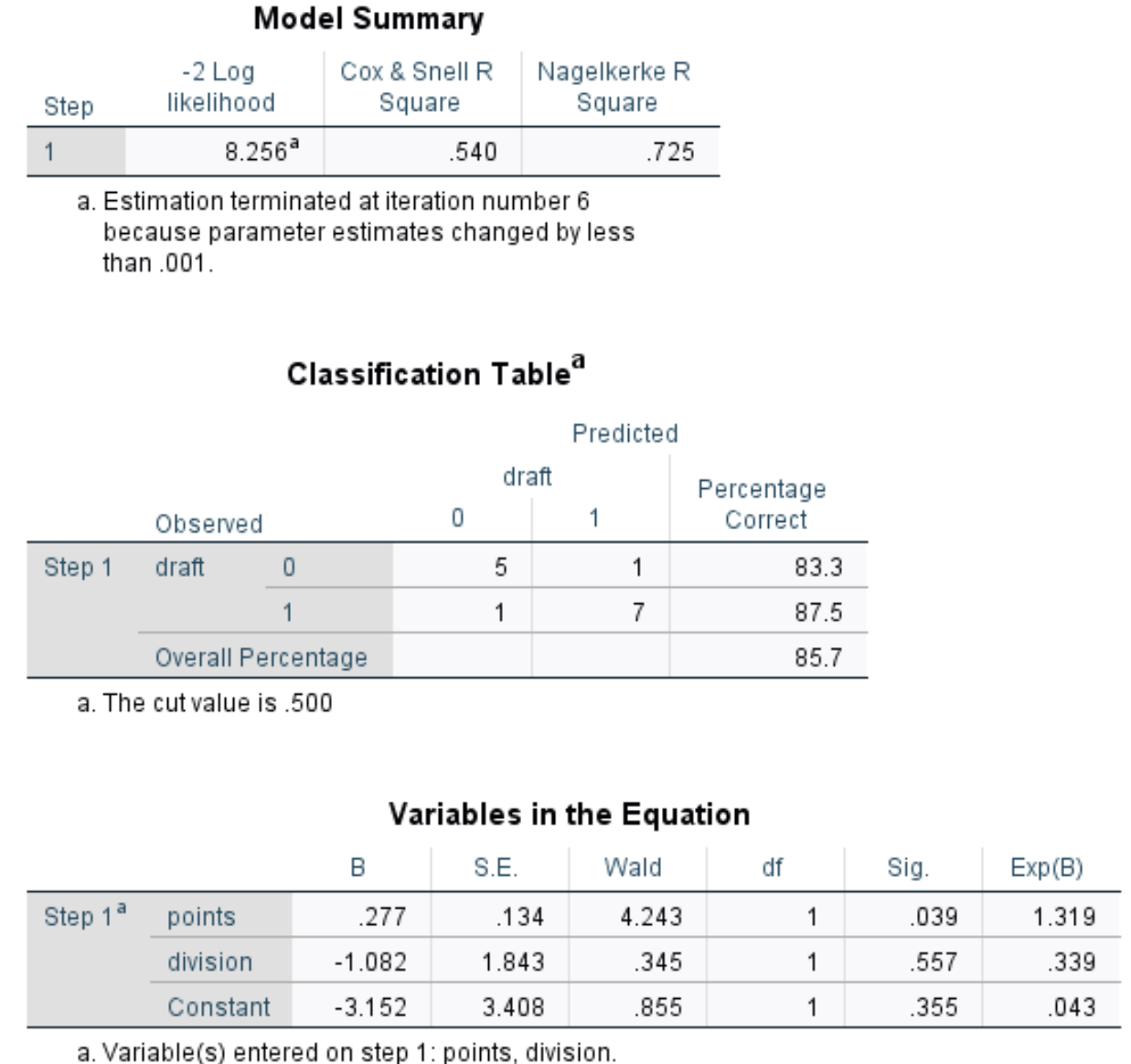
Sonucun nasıl yorumlanacağı aşağıda açıklanmıştır:

Model Özeti: Bu tablodaki en kullanışlı metrik, bize yanıt değişkenindeki yordayıcı değişkenler tarafından açıklanabilecek varyasyonun yüzdesini söyleyen Nagelkerke R Karesidir. Bu durumda puanlar ve bölünme draft değişkenliğinin %72,5’ini açıklayabilir.

Sınıflandırma tablosu: Bu tablodaki en kullanışlı ölçüm, modelin doğru şekilde sınıflandırabildiği gözlemlerin yüzdesini bize söyleyen genel yüzdedir. Bu durumda lojistik regresyon modeli, oyuncuların %85,7’sinin draft sonucunu doğru bir şekilde tahmin edebildi.

Denklemdeki değişkenler: Bu son tablo bize aşağıdakiler de dahil olmak üzere çeşitli yararlı ölçümler sağlar:

• Wald: Her yordayıcı değişkenin istatistiksel olarak anlamlı olup olmadığını belirlemek için kullanılan, her yordayıcı değişken için Wald testi istatistiği.
• Sig: Her yordayıcı değişken için Wald testi istatistiğine karşılık gelen p değeri. Puanlar için p değerinin 0,039, bölmenin p değerinin ise 0,557 olduğunu görüyoruz.
• Exp(B): Her öngörücü değişken için olasılık oranı. Bu bize, belirli bir tahmin değişkenindeki bir birimlik artışla bağlantılı olarak bir oyuncunun draft edilme ihtimalindeki değişimi anlatır. Örneğin, 2. Lig oyuncusunun draft edilme ihtimali, 1. Lig oyuncusunun draft edilme ihtimalinin yalnızca 0,339’udur. Benzer şekilde, maç başına puandaki her ek birim artış, bir oyuncunun draft edilme ihtimalinde 1.319’luk bir artışla ilişkilidir.

Daha sonra aşağıdaki formülü kullanarak belirli bir oyuncunun draft edilme olasılığını tahmin etmek için katsayıları (B etiketli sütundaki değerler) kullanabiliriz:

Olasılık = e ^{-3,152 + 0,277 (puan) – 1,082 (bölme)} / (1+e ^{-3,152 + 0,277 (puan) – 1,082 (bölme)} )

Örneğin maç başına ortalama 20 sayı atan ve 1.Lig’de oynayan bir oyuncunun draft edilme olasılığı şu şekilde hesaplanabilir:

Olasılık = e ^{-3,152 + 0,277(20) – 1,082(1)} / (1+e ^{-3,152 + 0,277(20) – 1,082(1)} ) ) = 0,787 .

Bu olasılık 0,5’ten büyük olduğundan bu oyuncunun draft edileceğini tahmin ediyoruz.

Adım 4. Sonuçları rapor edin.

Son olarak lojistik regresyonumuzun sonuçlarını bildirmek istiyoruz. İşte bunun nasıl yapılacağına dair bir örnek:

Oyun başına puanların ve bölüm seviyesinin bir basketbolcunun draft edilme olasılığını nasıl etkilediğini belirlemek için lojistik regresyon uygulandı. Analizde toplam 14 oyuncu kullanıldı.

Model, proje sonucundaki değişkenliğin %72,5’ini açıkladı ve vakaların %85,7’sini doğru şekilde sınıflandırdı.

Bir Division 2 oyuncusunun draft edilme ihtimali, Division 1 oyuncusunun draft edilme ihtimalinin yalnızca 0,339’uydu.

Maç başına puandaki her ek birim artış, bir oyuncunun draft edilme ihtimalinde 1.319 artışla ilişkilendirildi.