Google e-tablolar'daki standart sapma (örnek ve popülasyon)
Standart sapma, bir veri kümesindeki değerlerin dağılımını ölçmenin en yaygın yollarından biridir.
Üzerinde çalıştığınız veri türüne bağlı olarak hesaplayabileceğiniz iki farklı standart sapma türü vardır.
1. Nüfus standart sapması
Çalıştığınız veri seti tüm popülasyonu yani ilgilendiğiniz her değeri temsil ediyorsa popülasyon standart sapmasını hesaplamanız gerekir.
σ ile gösterilen popülasyon standart sapmasını hesaplama formülü şöyledir:
σ = √ Σ(x ben – μ) 2 / N
Altın:
- Σ : “Toplam” anlamına gelen bir sembol
- x i : Bir veri kümesindeki i’inci değer
- μ : Nüfus ortalaması
- N : Nüfus büyüklüğü
2. Standart sapma örneği
Üzerinde çalıştığınız veri seti daha büyük bir popülasyondan alınan bir örneği temsil ediyorsa, örnek standart sapmasını hesaplamanız gerekir.
Örnek standart sapmanın hesaplanmasına yönelik formül (s ile gösterilir):
s = √ Σ(x ben – x̄) 2 / (n – 1)
Altın:
- Σ : “Toplam” anlamına gelen bir sembol
- x i : Bir veri kümesindeki i’inci değer
- x̄ : Örnek şu anlama gelir:
- n : Örneklem büyüklüğü
Aşağıdaki örnekler Google E-Tablolar’da örnek ve popülasyon standart sapmasının nasıl hesaplanacağını göstermektedir.
Örnek 1: Google E-Tablolar’da örnek standart sapmanın hesaplanması
Bir biyoloğun belirli bir kaplumbağa türünün ağırlığının standart sapmasını özetlemek istediğini ve bu nedenle popülasyondan 20 kaplumbağadan oluşan basit rastgele bir örnek aldığını varsayalım.
Popülasyon standart sapmasını tahmin etmek için bir örnek kullandığından, örnek standart sapmasını hesaplayabilir.
Aşağıdaki ekran görüntüsü, örnek standart sapmayı hesaplamak için STDEV.S() işlevinin nasıl kullanılacağını gösterir:
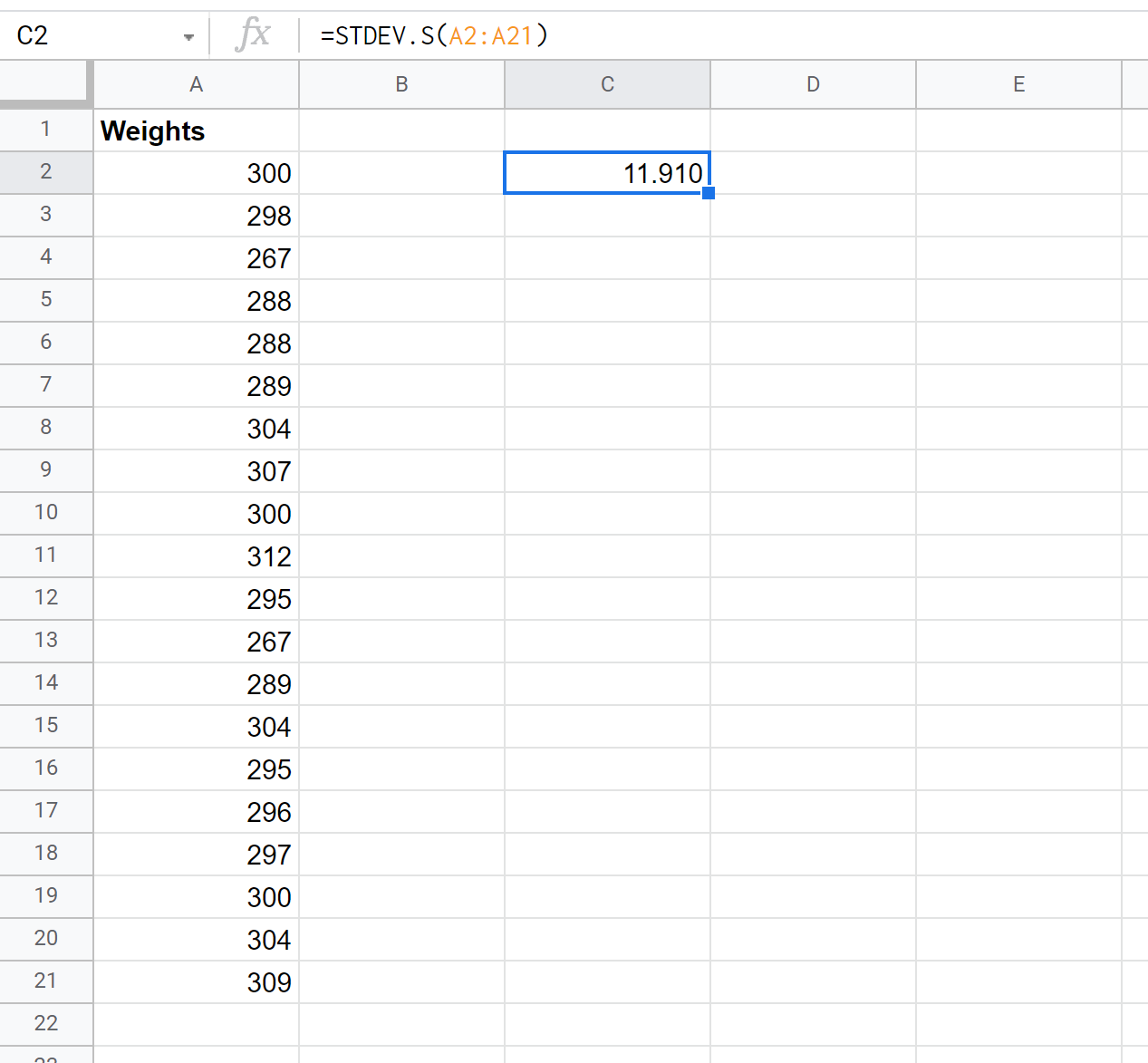
Örneklem standart sapması 11,91 olarak çıkıyor.
STDSAPMA() işlevinin aynı zamanda örnek standart sapmasını da döndüreceğini unutmayın.
Örnek 2: Google E-Tablolar’da Nüfus Standart Sapmasını Hesaplama
Bir basketbol antrenörünün, takımındaki 12 oyuncunun attığı sayıların standart sapmasını özetlemek istediğini varsayalım.
Başka bir takımdaki diğer oyuncuların değil, yalnızca kendi oyuncularının attığı puanlarla ilgilendiği için popülasyon standart sapmasını hesaplayabilir.
Aşağıdaki ekran görüntüsü popülasyon standart sapmasını hesaplamak için STDEV.P() işlevinin nasıl kullanılacağını gösterir:
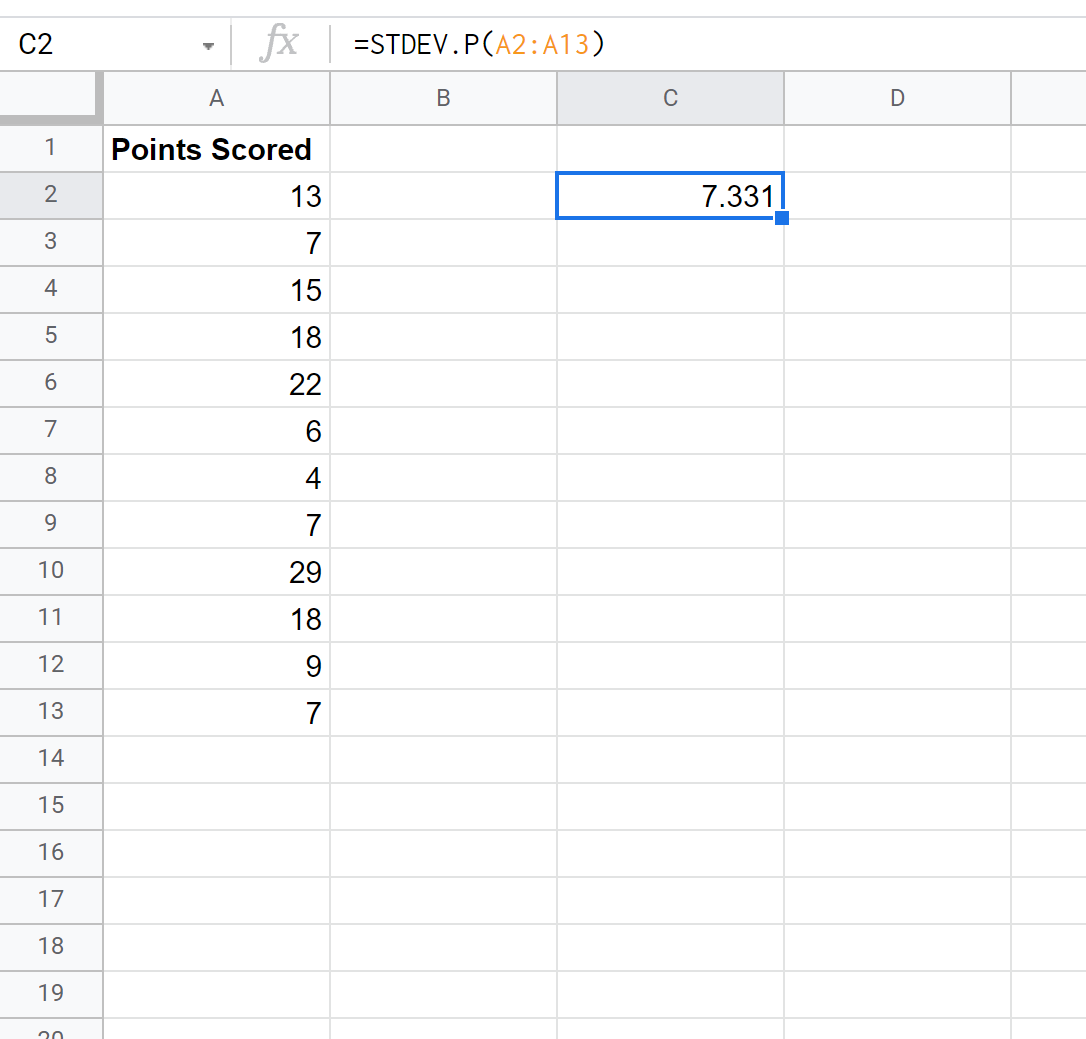
Popülasyonun standart sapması 7,331 olarak çıkıyor.
Ek kaynaklar
Aşağıdaki eğitimler standart sapma hakkında ek bilgi sağlar:
- Nüfus vs. Örnek Standart Sapma: Her Biri Ne Zaman Kullanılmalı
- Standart sapmaya karşı varyasyon katsayısı: fark
- Standart sapma neden önemlidir?
Aşağıdaki eğitimlerde Google E-Tablolar’daki diğer spread metriklerinin nasıl hesaplanacağı açıklanmaktadır:
yazar hakkında
Dr.benjamin anderson
Merhaba, ben Benjamin, emekli bir istatistik profesörü ve Statorials öğretmenine dönüştüm. İstatistik alanındaki kapsamlı deneyimim ve uzmanlığımla, öğrencilerimi Statorials aracılığıyla güçlendirmek için bilgilerimi paylaşmaya can atıyorum. Daha fazlasını bil