Standart sapma neden önemlidir? (açıklama + örnekler)

Standart sapma, bir numunedeki değerlerin dağılımını ölçmek için kullanılır.

Belirli bir örneğin standart sapmasını hesaplamak için aşağıdaki formülü kullanabiliriz:

√ Σ(x _i – x _çubuk ) ² / (n-1)

Altın:

• Σ: “toplam” anlamına gelen bir sembol
• x _i : örneğin ^i’inci değeri
• x _çubuğu : Örnek şu anlama gelir:
• n: Örneklem büyüklüğü

Standart sapma değeri ne kadar yüksek olursa, değerler bir numunede o kadar dağılmış demektir. Tersine, standart sapma değeri ne kadar düşükse değerler o kadar yakın kümelenir.

Öğrencilerin sıklıkla sorduğu soru şudur: Standart sapma neden önemlidir?

Cevap: Standart sapma önemlidir çünkü bize verilen bir veri setindeki değerlerin dağılımını anlatır.

bir veri kümesini analiz ettiğimizde, aşağıdaki ölçümleri bulmak isteriz:

• Veri kümesinin merkezi . “Merkezi” ölçmenin en yaygın yolu ortalama ve medyanı kullanmaktır.
• Veri kümesindeki değerlerin dağılımı . Yayılımı ölçmenin en yaygın yolu standart sapmayı kullanmaktır.

Merkezin nerede olduğunu ve değerlerin dağılımının ne olduğunu bilerek herhangi bir veri setindeki değerlerin dağılımını iyi anlayabiliriz.

Aşağıdaki örnekler standart sapmanın pratikteki önemini göstermektedir.

Örnek 1: Maaş dağıtımı

A şirketindeki ortalama maaşın 80.000 ABD Doları ve standart sapmanın 20.000 ABD Doları olduğunu varsayalım. Standart sapma çok büyük olduğundan, bu şirkette çalışırsanız yılda 80.000 dolara yakın maaş alacağınızın garantisi yok çünkü maaşlarda çok değişkenlik var.

Tersine, B Şirketindeki ortalama maaşın da 80.000 ABD Doları olduğunu, ancak standart sapmanın yalnızca 4.000 ABD Doları olduğunu varsayalım. Bu standart sapma çok küçük olduğu için maaşlarda çok az değişiklik olduğu için 80.000 dolara yakın maaş alacağınızdan emin olabilirsiniz.

Bu iki şirketteki maaş dağılımını görselleştirmek için bir kutu grafiği oluştursaydık şöyle görünebilirdi:

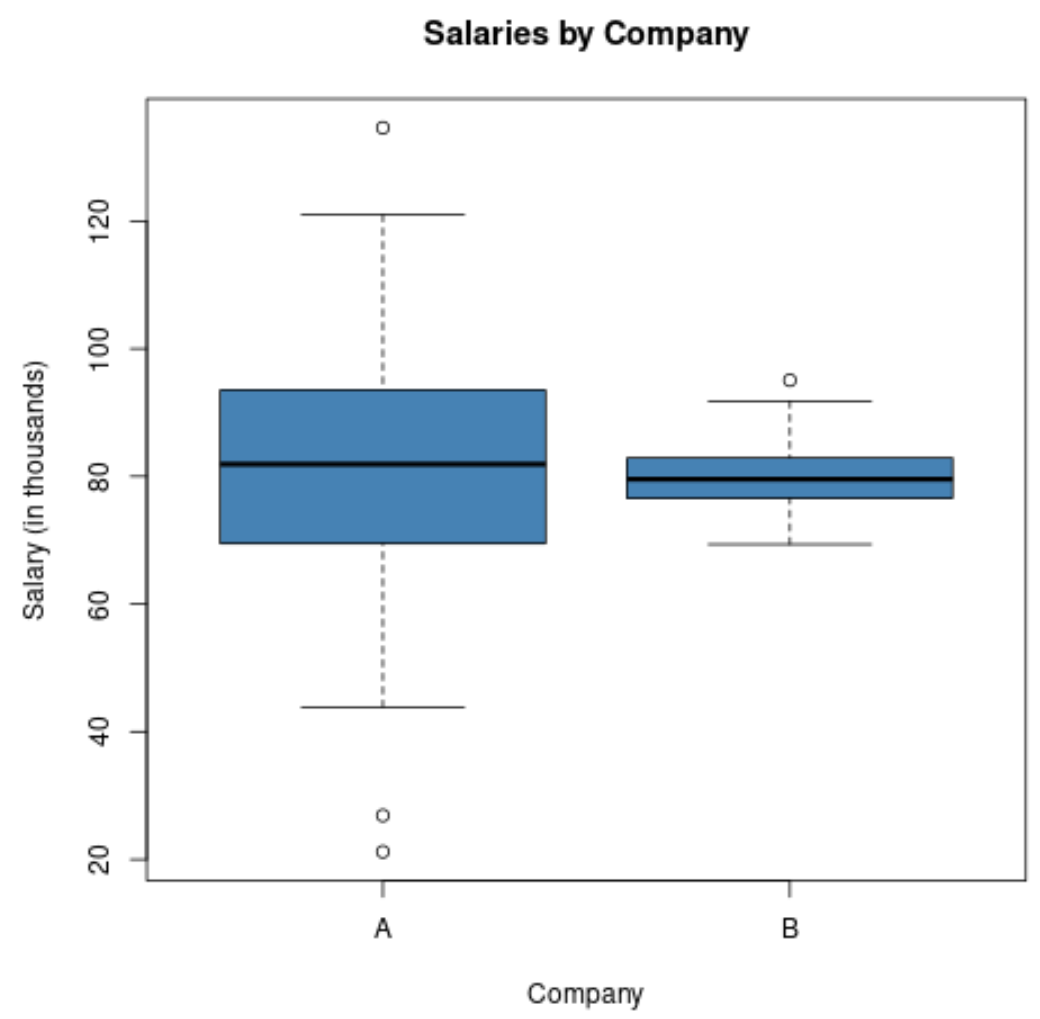
A şirketi için kutu grafiğinin uzunluğunun, ücretlerin standart sapması çok daha yüksek olduğundan daha büyük olduğuna dikkat edin.

Her iki şirket de aynı ortalama maaşa sahip ancak A şirketindeki maaş farkı çok daha yüksek.

Örnek 2: Konut fiyatlarının dağılımı

A mahallesindeki ortalama konut fiyatının 250.000$, standart sapmanın ise 50.000$ olduğunu varsayalım. Standart sapmanın oldukça büyük olması, bazı ev fiyatlarının 250.000 dolardan çok daha yüksek, bazılarının ise çok daha düşük olacağı anlamına geliyor. Bu mahalledeki herhangi bir eve baktığınızda fiyatın ortalamaya yakın olacağının garantisi yok.

Tersine, B mahallesindeki ortalama ev fiyatının da 250.000 $ olduğunu, ancak standart sapmanın yalnızca 10.000 $ olduğunu varsayalım. Bu standart sapma oldukça küçük olduğu için mahallede baktığınız her evin bu fiyata yakın olacağından emin olabilirsiniz.

Bu iki mahalledeki ev fiyatlarının dağılımını görselleştirmek için bir kutu grafiği oluştursaydık şöyle görünebilirdi:

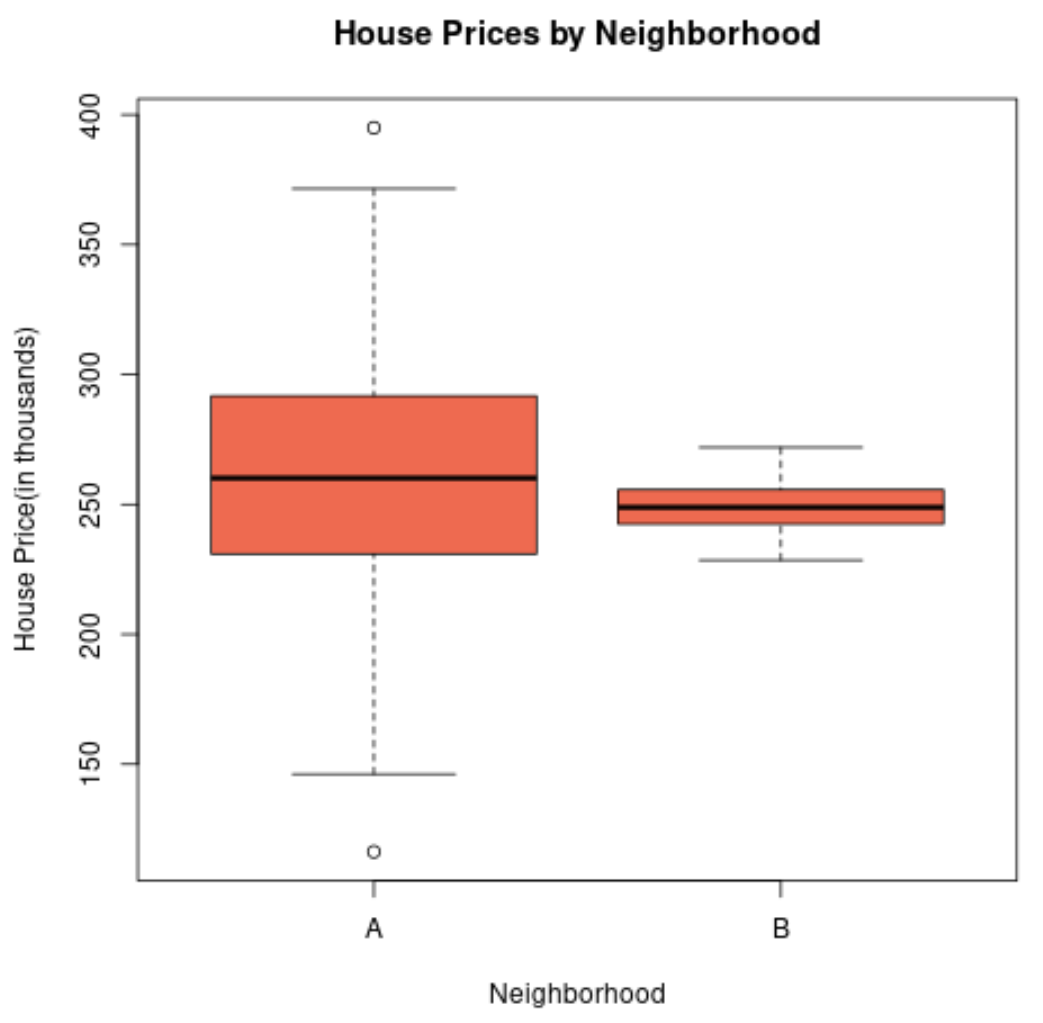
A mahallesinin parsel uzunluğu, gayrimenkul fiyatlarının standart sapması çok daha yüksek olduğundan daha büyüktür.

Aslında, A mahallesi için konut fiyatları 150.000 $’dan az ile 400.000 $’dan fazla arasında değişirken, B mahallesi için fiyatlar yalnızca 230.000 $ ile 270.000 $ arasında değişmektedir.

Her mahalledeki ev fiyatlarının standart sapmasını bilerek, her mahallede fiyatlarda ne kadar değişiklik bekleneceğini bilebiliriz.

Ek kaynaklar

İyi bir standart sapma olarak kabul edilen şey nedir?
Menzil vs. Standart Sapma: Her Biri Ne Zaman Kullanılmalı
Standart sapmaya karşı varyasyon katsayısı: fark