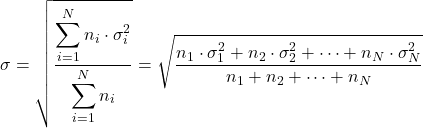Standart sapma (veya standart sapma)

İle Dr.benjamin anderson Ağustos 5, 2023 İstatistik 0 Yorum

Bu makalede standart sapma olarak da adlandırılan standart sapmanın ne olduğu açıklanmaktadır. Herhangi bir veri örneğinin standart sapmasını bulmak için standart sapmanın nasıl hesaplanacağını, adım adım pratik bir örneği ve çevrimiçi hesap makinesini öğreneceksiniz.

Standart sapma (veya standart sapma) nedir?

Standart sapma olarak da adlandırılan standart sapma , istatistiksel dağılımın bir ölçüsüdür. Başka bir deyişle standart sapma, bir dizi istatistiksel verinin dağılımını gösteren bir değerdir.

Bu nedenle standart sapma (veya standart sapma), bir popülasyonun veya istatistiksel numunenin dağılımını ölçmek için kullanılır. Bir veri serisinin standart sapması ne kadar büyük olursa, veriler o kadar dağınık olur. Yorum ters yönde de yapılabilir, eğer standart sapma düşükse bu, genel olarak verilerin ortalamaya çok yakın olduğu anlamına gelir.

Bir popülasyon üzerinden standart veya tipik sapma hesaplanırken standart sapmanın sembolü Yunanca sigma (σ) harfidir. Ancak örnek standart sapması söz konusu olduğunda istatistiksel ölçümü temsil etmek için s harfi kullanılır.

Bazı istatistik ve olasılık kitaplarında standart sapmaya standart sapma da denir.

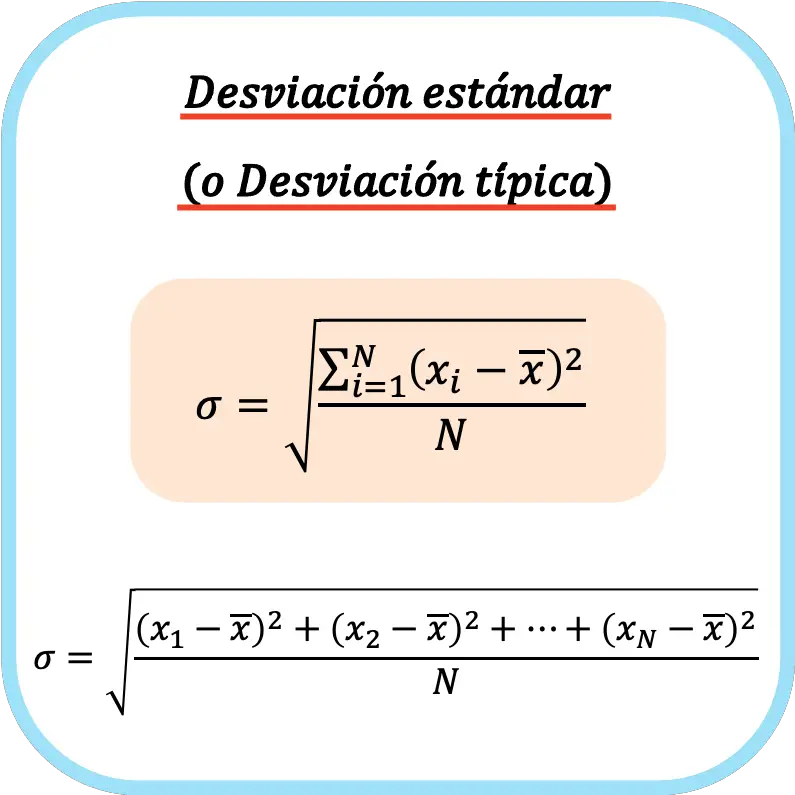
Standart sapma (veya standart sapma) formülü

Standart sapma (veya standart sapma), veri serisindeki sapmaların karelerinin toplamının karekökünün toplam gözlem sayısına bölünmesine eşittir.

Bu nedenle standart sapmayı (veya standart sapmayı) hesaplama formülü şu şekildedir:

👉Herhangi bir veri setinin standart sapmasını hesaplamak için aşağıdaki hesap makinesini kullanabilirsiniz.

Sonuç olarak, bir veri kümesinin standart sapmasını bulmak için tüm sapmaları (veri noktası ile aritmetik ortalama arasındaki fark olarak tanımlanır) hesaplamanız, sapmaları ikiye çıkarmanız, hepsini toplamanız ve ardından sayıya bölmeniz gerekir. Toplam. veri sayısını ve son olarak karekökünü alın.

Standart sapma örneği (veya standart sapma)

Aşağıda standart sapmanın (veya tipik sapmanın) tanımı göz önüne alındığında, bir veri serisinin standart sapmasının nasıl hesaplandığını görebilmeniz için adım adım bir örnek verilmiştir.

Aşağıdaki değerlerin standart sapmasını hesaplayın: 3, 6, 2, 9, 4.

Yapmamız gereken ilk şey örnek ortalamasını belirlemektir. Bunu yapmak için tüm verileri toplayıp toplam gözlem sayısına bölüyoruz ki bu da beştir:

$\overline{x}=\cfrac{3+6+2+9+4}{5}=4,8$

Şimdi standart sapma formülünü kullanıyoruz:

$\displaystyle\sigma=\sqrt{\frac{\displaystyle\sum_{i=1}^N(x_i-\overline{x})^2}{N}}$

Verileri formülde değiştiririz:

$\displaystyle\sigma =\sqrt{\frac{(3-4,8)^2+(6-4,8)^2+(2-4,8)^2+(9-4,8)^2+(4-4,8)^2}{5}}$

Son olarak standart sapmayı hesaplıyoruz:

$\begin{aligned}\displaystyle\sigma & = \sqrt{\frac{(-1,8)^2+1,2^2+(-2,8)^2+4,2^2+(-0,8)^2}{5}}\\[2ex]&=\sqrt{\frac{3,24+1,44+7,84+17,64+0,64}{5}}\\[2ex]&= \sqrt{\frac{30,8}{5}}=\sqrt{6,16}=2,48 \end{aligned}$

Standart Sapma (veya Standart Sapma) Hesaplayıcı

Standart sapmasını (veya standart sapmasını) hesaplamak için aşağıdaki çevrimiçi hesap makinesine bir dizi istatistiksel veri girin. Veriler bir boşlukla ayrılmalı ve ondalık ayırıcı olarak nokta kullanılarak girilmelidir.

Gruplandırılmış veriler için standart (veya tipik) sapma

Aralıklara göre gruplandırılmış verilerin standart sapmasını (veya standart sapmasını) hesaplamak için aşağıdaki adımlar izlenmelidir:

Gruplandırılmış verilerin ortalamasını bulun.
Gruplandırılmış verilerin sapmalarını hesaplayın.
Her boşluğun karesini alın.
Önceki her sonucu aralığının frekansıyla çarpın.
Önceki adımda elde edilen tüm değerlerin toplamını ekleyin.
Toplam gözlem sayısına bölün.
Önceki değerin karekökünü alın. Ortaya çıkan sayı, gruplandırılmış verilerin standart sapmasıdır.

Sonuç olarak, aralıklara göre gruplandırılmış verilerin standart sapmasını hesaplama formülü şöyledir:

$\displaystyle\sigma=\sqrt{\frac{\displaystyle\sum_{i=1}^N\left(x_i-\overline{x}\right)^2\cdot f_i }{N}}$

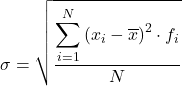
Normalde yukarıdaki formül kullanılsa da aynı sonuç elde edildiği için aşağıdaki cebirsel ifade de kullanılabilir:

$\displaystyle\sigma=\sqrt{\frac{\displaystyle\sum_{i=1}^n x_i^2\cdot f_i }{N}-\overline{x}^2}$

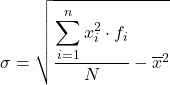
Bunun nasıl yapıldığını görebilirsiniz, aşağıda aralıklara göre gruplandırılmış verilerin standart sapmasına ilişkin adım adım bir alıştırma bulunmaktadır. Daha kesin olarak aşağıdaki istatistiksel verilerin standart sapması hesaplanacaktır:

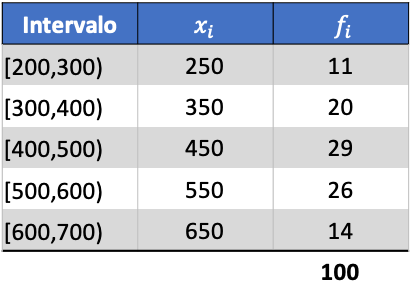
aralıklarla gruplandırılmış verilere örnek

Aritmetik ortalamayı hesaplamak için öncelikle her aralığın sınıf puanını frekansıyla çarpıyoruz:

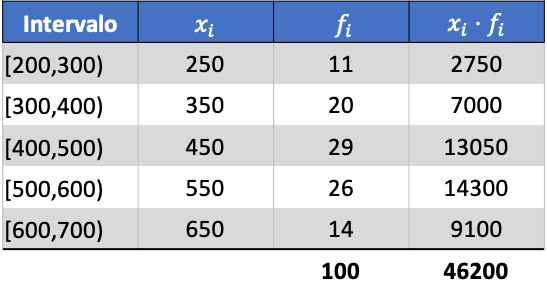
Yani gruplandırılmış verilerin ortalaması şöyle olacaktır:

$\overline{x}=\cfrac{\displaystyle\sum_{i=1}^n x_i\cdot f_i}{N}=\cfrac{46200}{100}=462$

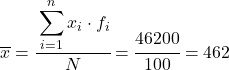
Artık ortalamanın değerini bildiğimize göre, aşağıdaki üç sütunu veri tablosuna eklememiz gerekiyor:

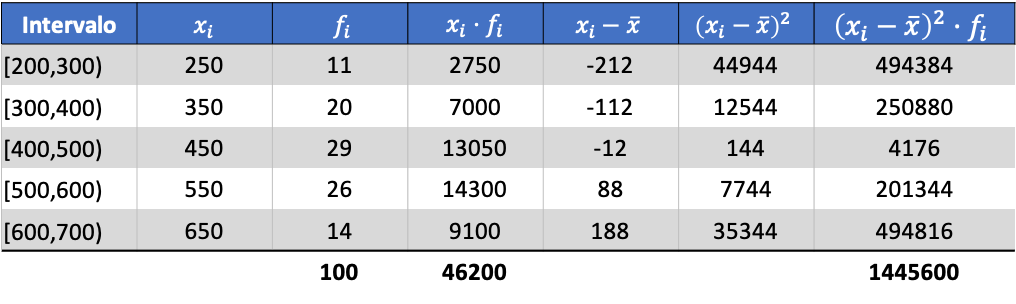
Gruplandırılmış veriler için standart sapma veya standart sapmanın çözümlü alıştırması

Daha sonra gruplandırılmış verilerin standart sapması, son sütunun toplamının karekökünün toplam gözlem sayısına bölünmesinin sonucu olacaktır:

$\displaystyle\sigma=\sqrt{\frac{\displaystyle\sum_{i=1}^N\left(x_i-\overline{x}\right)^2\cdot f_i }{N}}=\sqrt{\frac{1445600}{100}}=120,23$

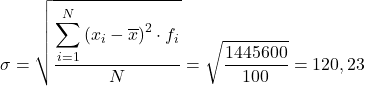
Standart (veya tipik) sapma ve varyans

Standart sapma (veya tipik sapma) ile varyans arasındaki ilişki, standart sapmanın varyansın karekökü olmasıdır.

Yani bir veri setinin varyans değerini biliyorsak karekökünü alarak standart sapmayı kolaylıkla hesaplayabiliriz. Ya da tam tersi, eğer standart sapmayı biliyorsak, değerin karesini alarak varyansı bulabiliriz.

$Var(X)=\sigma^2$

Aslında varyans, karesi alınmış standart sapma sembolü kullanılarak basit bir şekilde temsil edilebilir. Bu nedenle popülasyon varyansının sembolü sigma karedir (σ ² ) ve örneklem varyansının sembolü s karedir (s ² ).

Ek olarak, standart sapma ve varyans kavramları da benzer bir yoruma sahiptir çünkü her ikisi de bir dizi istatistiksel verinin dağılımını gösterir.

Standart sapmanın (veya standart sapmanın) özellikleri

Standart sapma aşağıdaki özelliklere sahiptir:

Bir veri örneğinin standart sapması negatif olamaz.

$\sigma \ge 0$

Tüm veriler aynıysa standart sapma sıfır olacaktır.

$\sigma =0$

Tüm verilere sabit terim eklenirse standart sapma değeri değişmez.

$\sigma (X+k)=\sigma (X)$

Tüm veriler bir sayıyla çarpılırsa standart sapma, söz konusu sayının mutlak değeriyle çarpılacaktır.

$\sigma (k\cdot X)=|k|\cdot \sigma (X)$

İki rastgele değişkenin toplamının standart sapması, değişkenlerin varyanslarının toplamının kareköküne artı iki değişken arasındaki kovaryansın iki katına eşittir.

$\sigma(X+Y)=\sqrt{Var(X)+Var(Y)+2\cdot Cov(X,Y)}$

Farklı dağılımların standart sapmalarını ( _σi ) ve veri sayısını ( _ni ) biliyorsak, aşağıdaki formülü uygulayarak toplam standart sapmayı hesaplayabiliriz:

$\displaystyle\sigma=\sqrt{\frac{\displaystyle \sum_{i=1}^N n_i\cdot \sigma_i^2}{\displaystyle \sum_{i=1}^N n_i}}=\sqrt{\frac{\displaystyle n_1\cdot \sigma_1^2+n_2\cdot \sigma_2^2+\dots +n_N\cdot \sigma_N^2}{\displaystyle n_1+n_2+\dots+n_N}}$

yazar hakkında

Dr.benjamin anderson

Merhaba, ben Benjamin, emekli bir istatistik profesörü ve Statorials öğretmenine dönüştüm. İstatistik alanındaki kapsamlı deneyimim ve uzmanlığımla, öğrencilerimi Statorials aracılığıyla güçlendirmek için bilgilerimi paylaşmaya can atıyorum. Daha fazlasını bil