İstatistikte süreklilik düzeltmesinin basit bir açıklaması
Süreklilik düzeltmesi, ayrık bir dağılıma yaklaşmak için sürekli bir dağılım kullanmak istediğinizde uygulanır. Genellikle, binom dağılımına yaklaşmak için normal dağılım kullanmak istediğinizde kullanılır.
Tek bir denemede başarı olasılığının p olduğu göz önüne alındığında, binom dağılımının bize n denemede x başarıya ulaşma olasılığını söylediğini hatırlayın. Olasılıkla ilgili soruları bir binom dağılımıyla yanıtlamak için, basitçe bir binom dağılım hesaplayıcısı kullanabiliriz, ancak aynı zamanda süreklilik düzeltmeli bir normal dağılım kullanarak da olasılığı yaklaşık olarak tahmin edebiliriz.
Süreklilik düzeltmesi, ayrık bir x değerine 0,5 ekleme veya çıkarma işlemine verilen addır.
Örneğin, bir paranın 100 atışta 45 kereden az veya buna eşit tura gelme olasılığını bulmak istediğimizi varsayalım. Yani P(X ≤ 45)’i bulmak istiyoruz. Binom dağılımına yaklaşmak amacıyla normal dağılımı kullanmak için bunun yerine P(X ≤ 45,5) buluruz.
Aşağıdaki tablo, bulmaya çalıştığınız olasılık türüne bağlı olarak ne zaman 0,5 eklemeniz veya çıkarmanız gerektiğini gösterir:
| Binom dağılımını kullanın | Süreklilik düzeltmesiyle normal dağılımın kullanılması |
|---|---|
| X = 45 | 44,5 < X < 45,5 |
| X ≤ 45 | X < 45,5 |
| X < 45 | X < 44,5 |
| X ≥ 45 | X > 44,5 |
| X > 45 | X > 45,5 |
Not:
Sadece n*p ve n*(1-p)’nin her ikisi de en az 5 olduğunda binom dağılımına yaklaşmak için normal dağılıma bir süreklilik düzeltmesi uygulamak uygundur.
Örneğin, n = 15 ve p = 0,6 olduğunu varsayalım. Bu durumda:
n*p = 15 * 0,6 = 9
n*(1-p) = 15 * (1 – 0,6) = 15 * (0,4) = 6
Bu sayıların her ikisi de 5’ten büyük veya ona eşit olduğundan, bu senaryoda süreklilik düzeltmesinin uygulanması kabul edilebilir olacaktır.
Aşağıdaki örnek, binom dağılımına yaklaşmak için normal dağılıma süreklilik düzeltmesinin nasıl uygulanacağını göstermektedir.
Süreklilik düzeltmesinin uygulama örneği
Bir madeni paranın 100 atışta 43 veya daha az kez tura gelme olasılığını bilmek istediğimizi varsayalım. Bu durumda:
n = deneme sayısı = 100
X = başarı sayısı = 43
p = belirli bir denemede başarı olasılığı = 0,50
Bu sayıları binom dağılım hesaplayıcısına yerleştirip madalyonun 43 katı veya daha az tura gelme olasılığının 0,09667 olduğunu görebiliriz.
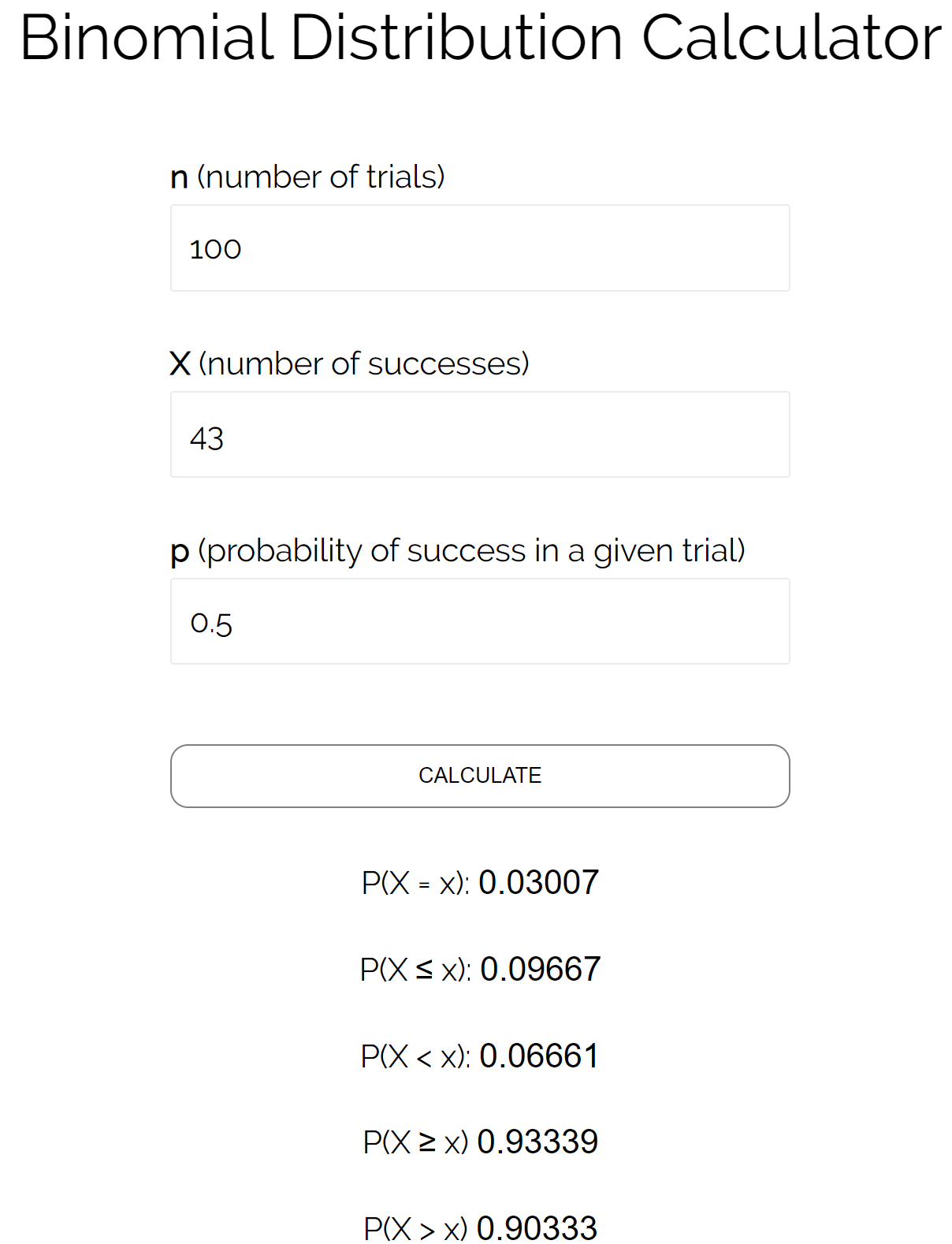
Normal dağılıma süreklilik düzeltmesi uygulayarak binom dağılımına yaklaşmak için aşağıdaki adımları kullanabiliriz:
Adım 1: n*p ve n*(1-p) öğelerinin her ikisinin de en az 5 olduğunu doğrulayın .
n*p = 100*0,5 = 50
n*(1-p) = 100*(1 – 0,5) = 100*0,5 = 50
Her iki sayı da 5’ten büyük veya eşittir, dolayısıyla devam edebiliriz.
Adım 2: 0,5’in eklenip çıkarılmayacağını belirleyin
Yukarıdaki tabloya bakıldığında X ≤ 43 şeklinde olasılık ile çalıştığımızda 0,5 eklememiz gerektiğini görüyoruz. Böylece P(X< 43,5) bulacağız.
Adım 3: Binom dağılımının ortalamasını (μ) ve standart sapmasını (σ) bulun.
µ = n*p = 100*0,5 = 50
σ = √ n*p*(1-p) = √ 100*.5*(1-.5) = √ 25 = 5
Adım 4: Önceki adımda bulunan ortalama ve standart sapmayı kullanarak z-puanını bulun.
z = (x – μ) / σ = (43,5 – 50) / 5 = -6,5 / 5 = -1,3.
Adım 5: Z puanıyla ilişkili olasılığı bulmak için Z tablosunu kullanın.
Tablo Z’ye göre z = -1,3 ile ilişkili olasılık 0,0968’dir .
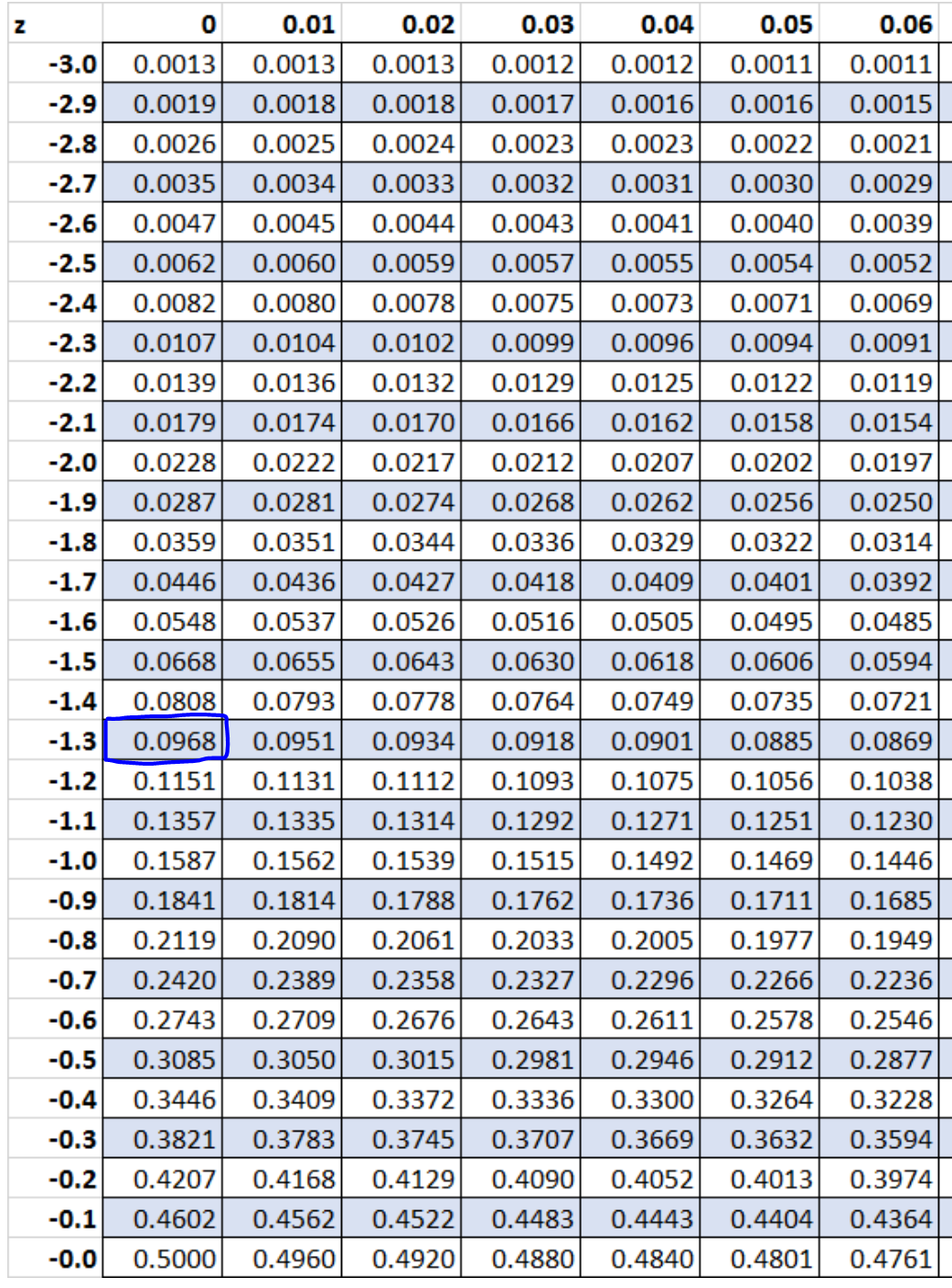
Yani binom dağılımını kullanarak bulduğumuz kesin olasılık 0,09667 iken, normal dağılımla süreklilik düzeltmesini kullanarak bulduğumuz yaklaşık olasılık 0,0968’di . Bu iki değer birbirine oldukça yakındır.
Süreklilik düzeltmesi ne zaman kullanılır?
Modern istatistiksel yazılımlar mevcut olmadan ve hesaplamaların manuel olarak yapılması gerekmeden önce, kesikli dağılımları içeren olasılıkları bulmak için süreklilik düzeltmeleri sıklıkla kullanılıyordu. Günümüzde süreklilik düzeltmeleri olasılıkların hesaplanmasında daha az rol oynuyor çünkü olasılıkları bizim için hesaplamak için genellikle yazılımlara veya hesap makinelerine güvenebiliyoruz.
Bunun yerine, bir binom dağılımı ile normal bir dağılım arasındaki ilişkiyi göstermek ve normal bir dağılımın bir süreklilik düzeltmesi uygulayarak bir binom dağılımına yaklaşmasının mümkün olduğunu göstermek, istatistik derslerinde ele alınan bir konudur.
Süreklilik düzeltme hesaplayıcısı
Binom olasılıklarını yaklaşık olarak normal dağılıma otomatik olarak bir süreklilik düzeltmesi uygulamak için süreklilik düzeltme hesaplayıcısını kullanın.