İstatistiklerde t değerleri ile p değerleri arasındaki fark

Öğrencilerin istatistikte sıklıkla karıştırdığı iki terim t değerleri ve p değerleridir .

Bu terimler arasındaki farkı anlamak için t-testlerini anlamak yardımcı olur.

Genel olarak konuşursak, üç farklı t testi türü vardır:

• Tek örnek t testi : Bir popülasyon ortalamasının belirli bir değere eşit olup olmadığını test etmek için kullanılır.
• İki örnekli t testi : İki popülasyonun ortalamalarının eşit olup olmadığını test etmek için kullanılır.
• Eşleştirilmiş örnekler t testi : Bir örnekteki her gözlem diğer örnekteki bir gözlemle ilişkilendirilebildiğinde iki popülasyonun ortalamalarının eşit olup olmadığını test etmek için kullanılır.

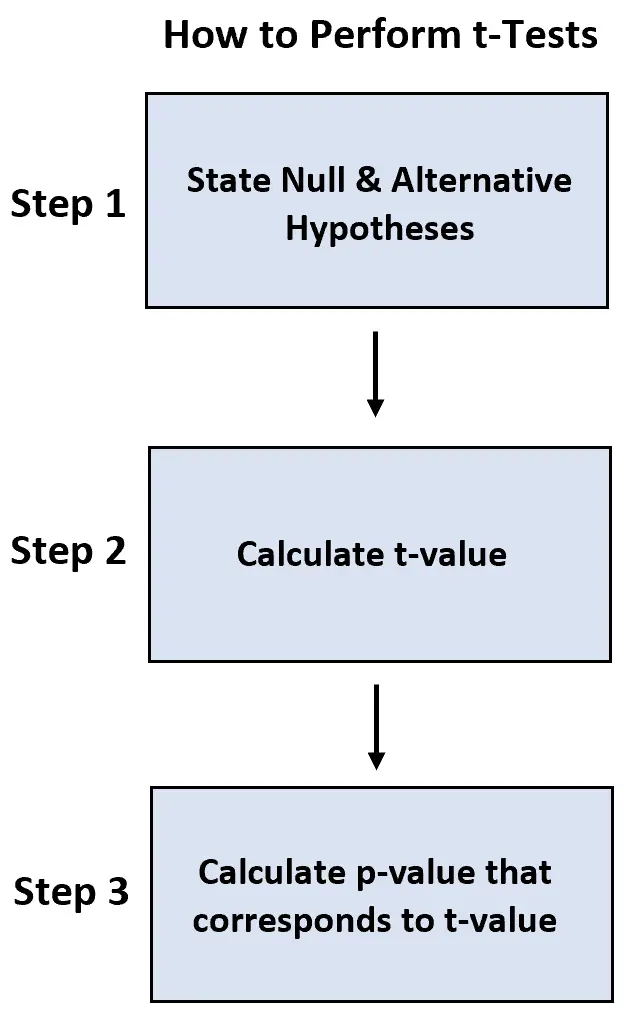
Her testi gerçekleştirmek için aşağıdaki adımları kullanırız:

• Adım 1: Boş ve alternatif hipotezleri belirtin.
• Adım 2: t değerini hesaplayın.
• Adım 3: T değerine karşılık gelen p değerini hesaplayın.

Her test için t değeri , popülasyon ortalamaları arasındaki farkı nicelleştirmenin bir yoludur ve p değeri, en azından ‘örnek’te gerçekten gözlemlediğimiz kadar büyük bir mutlak değere sahip bir t değeri elde etme olasılığıdır. Sıfır hipotezi gerçekten doğruysa veriler.

Eğer p değeri belirli bir değerden (örneğin 0,05) küçükse, testin sıfır hipotezini reddederiz.

Her bir t testi türü için p değeriyle ilgileniyoruz ve p değerini hesaplamak için sadece t değerini ara adım olarak kullanıyoruz.

Aşağıdaki örnek, iki örnekli bir t testi için bir t değerinin ve buna karşılık gelen p değerinin nasıl hesaplanacağını ve yorumlanacağını gösterir.

Örnek: T değerlerini ve P değerlerini hesaplayın ve yorumlayın

Diyelim ki iki farklı kaplumbağa türünün ortalama ağırlığının eşit olup olmadığını bilmek istiyoruz. Her popülasyondan aşağıdaki ağırlıklara sahip 12 kaplumbağadan oluşan basit rastgele bir örnek topluyoruz:

Tür #1 : 301, 298, 295, 297, 304, 305, 309, 298, 291, 299, 293, 304

Tür #2 : 302, 309, 324, 313, 312, 310, 305, 298, 299, 300, 289, 294

Bu verileri kullanarak iki örnekli bir t testinin nasıl gerçekleştirileceği aşağıda açıklanmıştır:

Adım 1: Boş ve alternatif hipotezleri belirtin.

Öncelikle boş ve alternatif hipotezleri belirtelim:

• H ₀ : μ ₁ = μ ₂ (iki popülasyon ortalaması eşittir)
• H ₁ : μ ₁ ≠ μ ₂ (iki popülasyon ortalaması eşit değildir)

Adım 2: t değerini hesaplayın.

Daha sonra, her bir kaplumbağa örneğinin ağırlığını iki örnekli t testi hesaplayıcısına gireceğiz ve t değerinin -1,608761 olduğunu bulacağız.

Adım 3: P değerini hesaplayın.

-1,608761 t değerine karşılık gelen p değerinin 0,121926 olduğunu bulmak için iki örnekli t testi hesaplayıcısını da kullanabiliriz.

Bu p değeri 0,05’ten küçük olmadığından sıfır hipotezini reddedemiyoruz.

Bu, iki popülasyon arasındaki kaplumbağaların ortalama ağırlığının farklı olduğunu söyleyecek yeterli kanıta sahip olmadığımız anlamına geliyor.

P değerini hesaplamak için t değerini ara adım olarak kullandığımızı unutmayın. P değeri ilgilendiğimiz gerçek değerdi ancak önce t değerini hesaplamamız gerekiyordu.

Ek kaynaklar

Aşağıdaki eğitimler t testleri ve p değerleri hakkında ek bilgi sunar:

Tek örnekli t-testine giriş
İki örnekli t testine giriş
Eşleştirilmiş örnekler t-testine giriş
Bir t testinden P değeri manuel olarak nasıl hesaplanır?