T-score ve z-score: ne zaman kullanılmalı?

İstatistik derslerinde öğrencilerin sıklıkla kafasını karıştıran iki terim t-puanları ve z-puanlarıdır .

Her ikisi de hipotez testi yaparken veya güven aralıkları oluştururken yaygın olarak kullanılır, ancak biraz farklıdırlar.

İşte her birinin formülü:

puan t = ( x – μ) / (s/√ n )

Altın:

• x : örnek ortalama
• μ : Nüfus ortalaması
• s : Örneklem standart sapması
• n : Örneklem büyüklüğü

z-puanı = ( x – μ) / σ

Altın:

• x : Ham veri değeri
• μ : Nüfus ortalaması
• σ : Nüfus standart sapması

Bu akış şeması, verilerinize göre her birini ne zaman kullanmanız gerektiğini gösterir:

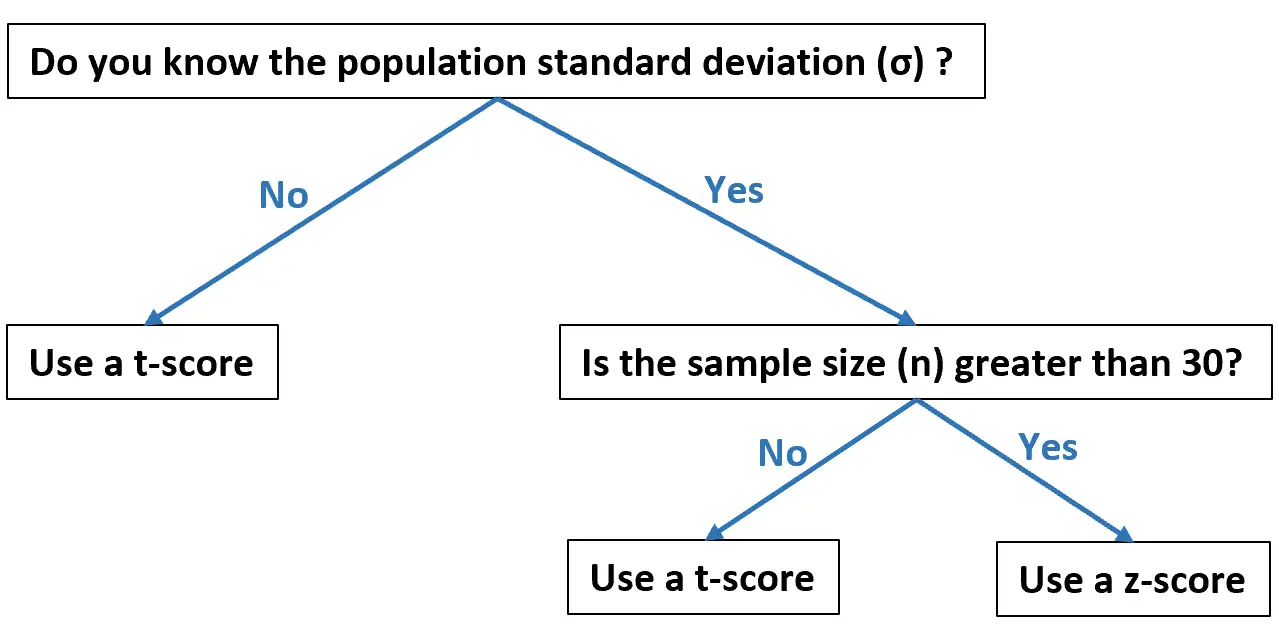
Aşağıdaki örneklerde T-puanı ve Z-puanının pratikte nasıl hesaplanacağı gösterilmektedir.

Örnek 1: T-Skorunun Hesaplanması

Bir restoranın ortalama ağırlığının μ = 0,25 pound olduğunu iddia ederek hamburger hazırladığını varsayalım.

N = 20 hamburgerden rastgele bir örnek aldığımızı ve örneğin ortalama ağırlığının x = 0,22 pound ve standart sapması s = 0,05 pound olduğunu bulduğumuzu varsayalım. Bu restoranın ürettiği tüm hamburgerlerin gerçek ortalama ağırlığının 0,25 pound olup olmadığını belirlemek için bir hipotez testi yapın.

Bu örnekte, aşağıdaki iki koşulun hiçbiri karşılanmadığı için hipotez testini gerçekleştirmek için bir T-puanı kullanacağız.

• Popülasyon standart sapması (σ) bilinmektedir. (bu örnekte σ sağlanmamıştır)
• Örneklem büyüklüğü 30’dan büyük. (Bu örnekte n=20)

Dolayısıyla t-puanını şu şekilde hesaplayabiliriz:

• puan t = ( x – μ) / (s/√ n )
• t-puanı = (0,22 – 0,25) / (0,05 / √ 20 )
• t-puanı = -2,68

P değeri T puanı hesaplayıcısına göre bu t puanına karşılık gelen p değeri 0,01481’dir .

Bu p değeri 0,05’ten küçük olduğundan, bu restoranda üretilen hamburgerlerin ortalama ağırlığının 0,25 pound’a eşit olmadığını söylemek için yeterli kanıtımız var.

Örnek 2: Z puanının hesaplanması

Bir şirketin, ömrü μ = 20 saat ve standart sapması σ = 5 saat olan normal bir dağılıma uyduğu bilinen piller ürettiğini varsayalım.

Diyelim ki n = 50 adet pilden rastgele bir örnek alıyoruz ve örnek ortalamasının x = 21 saat olduğunu buluyoruz. Bu şirket tarafından üretilen tüm pillerin gerçek ortalama ömrünün 20 saate eşit olup olmadığını belirlemek için bir hipotez testi yapın.

Bu örnekte, aşağıdaki koşulların her ikisi de karşılandığı için hipotez testini gerçekleştirmek için bir z-puanı kullanacağız:

• Popülasyon standart sapması (σ) bilinmektedir. (σ bu örnekte 5’e eşittir)
• Örneklem büyüklüğü 30’dan büyük. (Bu örnekte n=50)

Dolayısıyla z-puanını şu şekilde hesaplayabiliriz:

• z-puanı = ( x – μ) / σ
• z-puanı = (21 – 20) / 5
• z-puanı = 0,2

P değeri Z puanı hesaplayıcısına göre bu z puanına karşılık gelen p değeri 0,84184’tür .

Bu p değeri 0,05’ten az olmadığı için bu firmanın ürettiği tüm pillerin ortalama ömrünün 20 saatten farklı olduğunu söyleyecek yeterli kanıtımız yok.

Ek kaynaklar

Aşağıdaki eğitimler T puanları ve Z puanları hakkında daha fazla bilgi sunar:

Normal dağılım ve t dağılımı: fark nedir?
Dağıtım tablosu t nasıl okunur
Z tablosu nasıl okunur