Excel'de t puanından p değeri nasıl bulunur?

İstatistiklerde sıklıkla bir hipotez testi T-skoru testi istatistiğiyle sonuçlanır. Bu t-puanını bulduğumuzda genellikle onunla ilişkili p-değerini de buluruz. Eğer bu p değeri belirli bir alfa seviyesinin altındaysa (örneğin 0,10, 0,05, 0,01), testin sıfır hipotezini reddeder ve sonuçlarımızın anlamlı olduğu sonucuna varırız.

Bu eğitimde, aşağıdaki bağımsız değişkenleri alan T.DAĞ işlevini kullanarak Excel’de bir t-puanından p-değerinin nasıl bulunacağı açıklanmaktadır:

T.DAĞ (x, derece_serbestlik)

Altın:

• x: Bizi ilgilendiren T puanı.
• deg_freedom: Serbestlik dereceleri.

Hadi bazı örneklere bakalım.

Örnek 1: T-puanından P değeri (iki kuyruklu)

Bir botanikçi, belirli bir bitki türünün ortalama boyunun 15 inç olup olmadığını bilmek istiyor. 12 bitkiden oluşan rastgele bir örnekte , örneğin ortalama yüksekliğinin 14,33 inç ve örneğin standart sapmasının 1,37 inç olduğunu bulur.

Ortalama yüksekliğin 15 inç olup olmadığını belirlemek için 0,05 alfa düzeyini kullanarak iki kuyruklu bir hipotez testi yapın.

Adım 1: Hipotezleri belirtin.

Boş hipotez (H ₀ ): μ = 15

Alternatif hipotez: (Ha): μ ≠ 15

Adım 2: T-puanını ve serbestlik derecelerini bulun.

puan t = ( x -μ) / (s/√n) = (14,33-15) / (1,37/√12) = -1,694 .

serbestlik derecesi = n-1 = 12-1 = 11 .

Adım 3: Excel’i kullanarak t puanının p değerini bulun.

T puanının p değerini bulmak için Excel’de aşağıdaki formülü kullanacağız:

=T.DAĞ.2T(ABS(-1,694), 11)

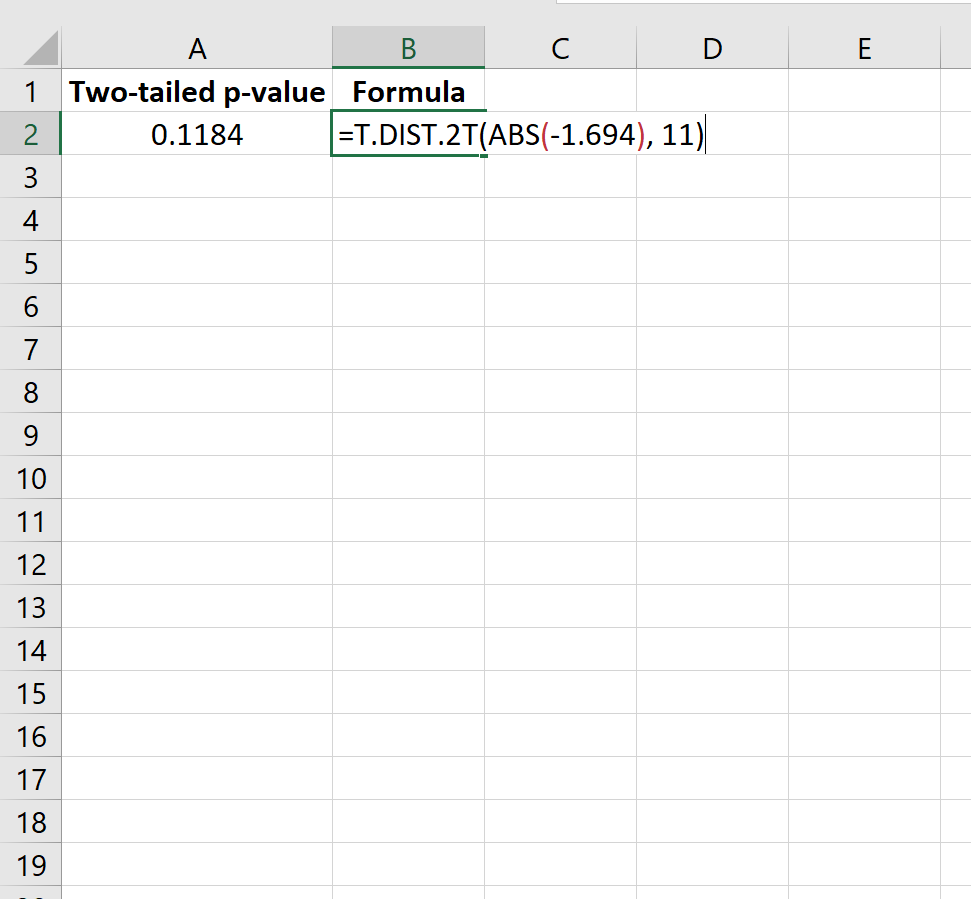
Bu bize iki taraflı p değerinin 0,1184 olduğunu söyler.

Adım 4: Sıfır hipotezini reddedin veya reddetmeyin.

0,1184’ün p değeri seçilen alfa seviyesinden 0,05’ten az olmadığından sıfır hipotezini reddetmede başarısız oluyoruz. Ortalama bitki boyunun 15 inçten farklı olduğunu söyleyecek yeterli kanıtımız yok.

Örnek 2: T skorundan P değeri (tek taraflı)

Bir şirket, yeni bir pil türünün, ortalama ömrü 18 saat olan mevcut standart pilden daha uzun bir ortalama ömre sahip olup olmadığını bilmek istiyor. 25 yeni pilden oluşan rastgele bir örnekte , ortalama ömrün 4 saatlik standart sapmayla 19 saat olduğunu buldular.

Yeni pilin ortalama ömrünün mevcut standart pilin ortalama ömründen daha uzun olup olmadığını belirlemek için 0,05 alfa düzeyini kullanarak tek taraflı bir hipotez testi yapın.

Adım 1: Hipotezleri belirtin.

Sıfır hipotezi (H ₀ ): μ ≤ 18

Alternatif hipotez: (Ha): μ > 18

Adım 2: T-puanını ve serbestlik derecelerini bulun.

puan t = ( x -μ) / (s/√n) = (19-18) / (4/√25) = 1,25 .

serbestlik derecesi = n-1 = 25-1 = 24 .

Adım 3: Excel’i kullanarak t puanının p değerini bulun.

T puanının p değerini bulmak için Excel’de aşağıdaki formülü kullanacağız:

=T.DAĞ.RT(1,25, 24)

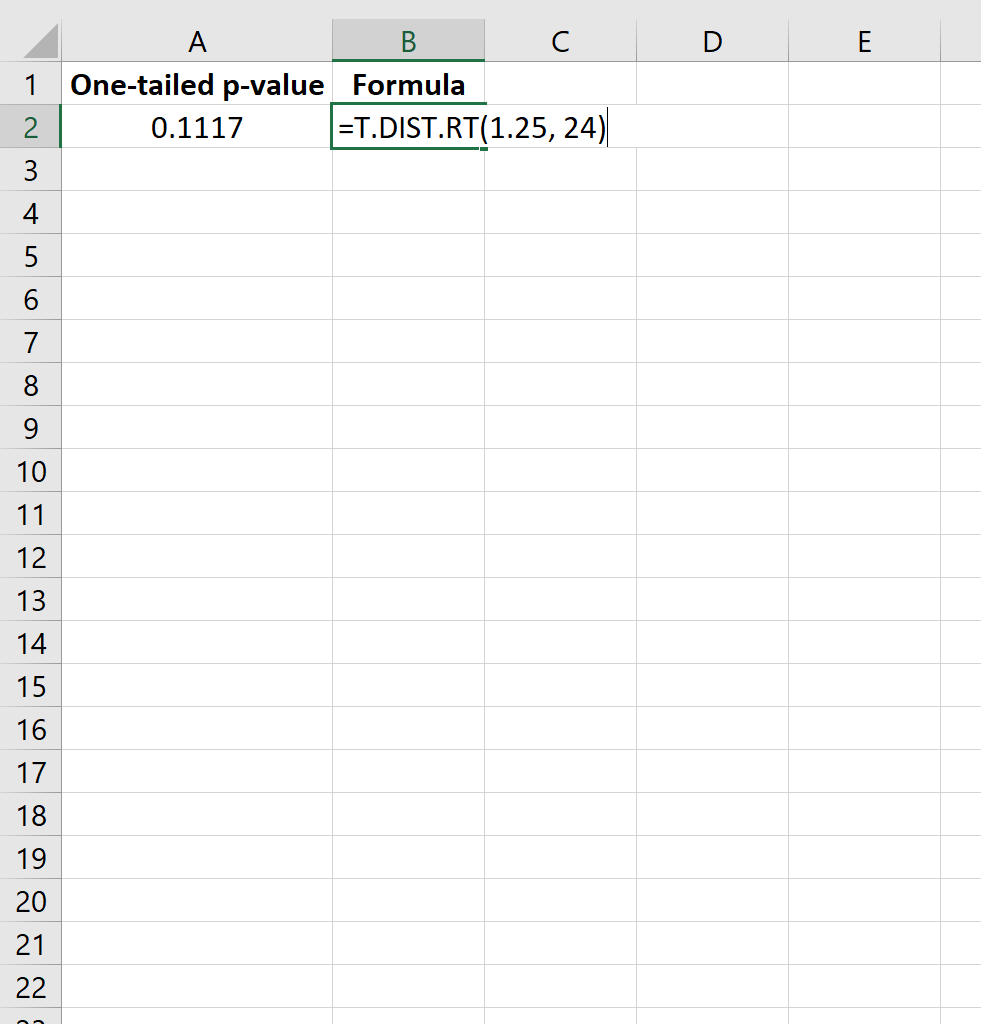
Bu bize tek taraflı p değerinin 0,1117 olduğunu söyler.

Adım 4: Sıfır hipotezini reddedin veya reddetmeyin.

0,1117’lik p değeri, seçilen 0,05 alfa düzeyinden daha büyük olduğundan, sıfır hipotezini reddetmede başarısız oluyoruz. Yeni pilin ortalama ömrünün mevcut standart pilin ortalama ömründen daha uzun olduğunu söyleyecek yeterli kanıtımız yok.

Excel’deki istatistiklerle ilgili daha fazla eğitim için Excel kılavuzlarının tam listesine göz atmayı unutmayın .