Tanımlayıcı veya çıkarımsal istatistikler: fark nedir?

İstatistik alanında iki ana dal vardır:

• Tanımlayıcı istatistikler
• Çıkarımsal istatistik

Bu eğitimde iki dal arasındaki fark ve her birinin belirli durumlarda neden yararlı olduğu açıklanmaktadır.

Tanımlayıcı istatistikler

Özetle, tanımlayıcı istatistikler , özet istatistikler, grafikler ve tablolar kullanarak bir dizi ham veriyi tanımlamayı amaçlamaktadır.

Tanımlayıcı istatistikler faydalıdır çünkü bir grup veriyi yalnızca ham veri değerlerinin satırlarına bakmaktan çok daha hızlı ve kolay bir şekilde anlamanıza olanak tanırlar.

Örneğin, belirli bir okuldaki 1000 öğrencinin sınav puanlarını gösteren ham bir veri setimiz olduğunu varsayalım. Ortalama test puanının yanı sıra test puanlarının dağılımı da ilgimizi çekebilir.

Tanımlayıcı istatistikleri kullanarak ortalama puanı bulabilir ve puanların dağılımını görselleştirmemize yardımcı olacak bir grafik oluşturabiliriz.

Bu, öğrencilerin test puanlarını ham verilere bakmaktan çok daha kolay anlamamızı sağlar.

Tanımlayıcı istatistiklerin yaygın biçimleri

Tanımlayıcı istatistiklerin üç yaygın biçimi vardır:

1. Özet istatistikler. Verileri tek bir sayı kullanarak özetleyen istatistiklerdir. İki yaygın özet istatistik türü vardır:

• Merkezi eğilim ölçüleri : Bu sayılar bir veri kümesinin merkezinin nerede olduğunu tanımlar. Örnekler arasında ortalama   ve medyan .
• Dağılım ölçüleri: Bu sayılar veri setindeki değerlerin dağılımını tanımlar. Örnekler arasında aralık , çeyrekler arası aralık , standart sapma ve varyans yer alır.

2. Grafikler . Grafikler verileri görselleştirmemize yardımcı olur. Verileri görselleştirmek için kullanılan yaygın grafik türleri arasında kutu grafikleri , histogramlar , gövde ve yaprak grafikleri ve dağılım grafikleri bulunur.

3. Tablolar . Tablolar verilerin nasıl dağıtıldığını anlamamıza yardımcı olabilir. Yaygın bir tablo türü, bize kaç veri değerinin belirli aralıklara düştüğünü söyleyen frekans tablosudur .

Tanımlayıcı istatistikleri kullanma örneği

Aşağıdaki örnek, tanımlayıcı istatistikleri gerçek dünyada nasıl kullanabileceğimizi göstermektedir.

Belirli bir okuldaki 1000 öğrencinin hepsinin aynı sınava girdiğini varsayarız. Test sonuçlarının dağılımını anlamak istediğimiz için aşağıdaki tanımlayıcı istatistikleri kullanıyoruz:

1. Özet istatistikler

Ortalama: 82.13 . Bu bize 1000 öğrenci arasındaki ortalama test puanının 82,13 olduğunu söylüyor.

Medyan: 84. Bu bize öğrencilerin yarısının 84’ün üzerinde, diğer yarısının ise 84’ün altında puan aldığını gösteriyor.

Maksimum: 100. Min: 45. Bu bize herhangi bir öğrencinin alabileceği maksimum puanın 100, minimum puanın ise 45 olduğunu söyler. Maksimum ile minimum arasındaki farkı gösteren aralık 55’tir.

2. Grafikler

Test sonuçlarının dağılımını görselleştirmek için, frekansları temsil etmek için dikdörtgen çubuklar kullanan bir tür grafik olan histogram oluşturabiliriz.

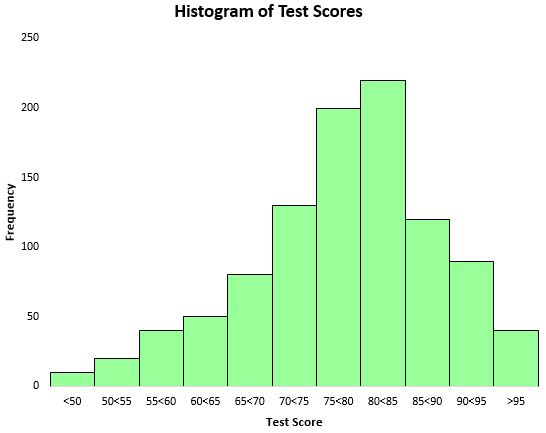
Bu histograma dayanarak test puanlarının dağılımının kabaca çan şeklinde olduğunu görebiliriz. Çoğu öğrenci 70 ila 90 arasında puan alırken, çok azı 95’in üzerinde puan alırken, çok azı 50’nin altında puan aldı.

3. Tablolar

Puanların dağılımını anlamanın bir diğer kolay yolu da frekans tablosu oluşturmaktır. Örneğin, aşağıdaki frekans tablosu farklı aralıklarda puan alan öğrencilerin yüzdesini göstermektedir:

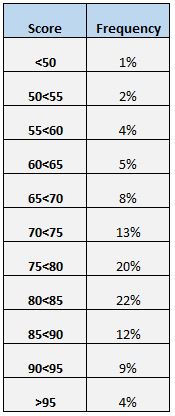
Toplam öğrencilerin yalnızca %4’ünün 95’in üzerinde puan aldığını görüyoruz. Ayrıca (%12 + %9 + %4 = ) tüm öğrencilerin %25’inin 85 veya üzerinde puan aldığını da görebiliyoruz.

Veri değerlerinin yüzde kaçının belirli bir değerin üstünde veya altında olduğunu bilmek istiyorsak, frekans tablosu özellikle kullanışlıdır. Örneğin, okulun 75’in üzerindeki herhangi bir puanı “kabul edilebilir” bir test puanı olarak değerlendirdiğini varsayalım.

Frekans tablosuna baktığımızda (%20 + %22 + %12 + %9 + %4 =) öğrencilerin %67’sinin testten kabul edilebilir bir puan aldığını rahatlıkla görebiliriz.

Çıkarımsal istatistik

Özetle, çıkarımsal istatistikler, örneğin alındığı daha büyük popülasyon hakkında sonuçlar çıkarmak için küçük bir veri örneğini kullanır.

Örneğin bir ülkedeki milyonlarca insanın siyasi tercihlerini anlamak isteyebiliriz.

Ancak ülkedeki her bireyi araştırmak çok zaman alıcı ve pahalı olacaktır. Bunun yerine, örneğin 1000 Amerikalıyla daha küçük bir anket yapacağız ve anket sonuçlarını bir bütün olarak nüfus hakkında sonuçlar çıkarmak için kullanacağız.

Çıkarımsal istatistiklerin tüm dayanağı budur: Bir popülasyon hakkındaki bir soruyu yanıtlamak istiyoruz, dolayısıyla o popülasyonun küçük bir örneği için veri elde ediyoruz ve örnek verileri popülasyon hakkında çıkarımlar yapmak için kullanıyoruz.

Temsili bir numunenin önemi

Bir popülasyon hakkında sonuç çıkarmak amacıyla bir örneklem kullanma yeteneğimizden emin olmak için, temsili bir örneklemimiz olduğundan, yani popülasyondaki bireylerin özelliklerinin bulunduğu bir örneklemden emin olmalıyız. Örnek, örnekle yakından eşleşiyor. özellikleri. genel nüfusun.

İdeal olarak, örneğimizin popülasyonumuzun “mini versiyonuna” benzemesini istiyoruz. Bu nedenle, %50’si kızlardan ve %50’si erkeklerden oluşan bir öğrenci popülasyonu hakkında sonuç çıkarmak istersek, örneklemimiz %90’ı erkek ve yalnızca %10’u kızlardan oluşuyorsa temsili olmayacaktır.

Örneğimiz genel nüfusa benzemiyorsa, örneklemden elde edilen sonuçları genel nüfusa güvenle genelleştiremeyiz.

Temsili bir numune nasıl elde edilir

Temsili bir numune alma şansını en üst düzeye çıkarmak için iki şeye odaklanmalısınız:

1. Rastgele örnekleme yöntemi kullandığınızdan emin olun.

Temsili bir örnek üretmesi muhtemel olan, kullanabileceğiniz çeşitli rastgeleörnekleme yöntemleri vardır:

• Basit bir rastgele örnek
• Sistematik rastgele bir örnek
• Bir küme rastgele örneği
• Tabakalı rastgele bir örnek

Rastgele örnekleme yöntemleri temsili örnekler üretme eğilimindedir çünkü popülasyonun her üyesinin örneğe dahil edilme şansı eşittir.

2. Örneklem büyüklüğünüzün yeterince büyük olduğundan emin olun .

Uygun bir örnekleme yöntemi kullanmanın yanı sıra, daha büyük bir popülasyona genelleme yapabilmek için yeterli veriye sahip olmanız için örneklemin yeterince büyük olmasını sağlamak önemlidir.

Örneklem büyüklüğünüzü belirlemek için, üzerinde çalıştığınız popülasyonun büyüklüğünü, kullanmak istediğiniz güven düzeyini ve kabul edilebilir olduğunu düşündüğünüz hata marjını dikkate almanız gerekir.

Neyse ki bu değerleri girmek için çevrimiçi hesap makinelerini kullanabilir ve örnek boyutunuzun ne olması gerektiğini görebilirsiniz.

Çıkarımsal istatistiklerin yaygın biçimleri

Çıkarımsal istatistiklerin üç yaygın biçimi vardır:

1. Hipotez testi.

Genellikle bir popülasyonla ilgili aşağıdaki gibi soruları yanıtlamak isteriz:

• Ohio’da Aday A’yı destekleyenlerin yüzdesi %50’den fazla mı?
• Belirli bir bitkinin ortalama yüksekliği 14 inç’e eşit mi?
• A okulu ile B okulundaki öğrencilerin ortalama boyları arasında fark var mıdır?

Bu soruları yanıtlamak için, bir örneklemden elde edilen verileri kullanarak popülasyonlar hakkında sonuçlar çıkarmamıza olanak tanıyan hipotez testi gerçekleştirebiliriz.

2. Güven aralıkları .

Bazen bir popülasyon için belirli bir değeri tahmin etmek isteriz. Örneğin Avustralya’daki belirli bir bitki türünün ortalama boyuyla ilgilenebiliriz.

Ülkedeki her bitkiyi dolaşıp ölçmek yerine, bitkilerden küçük bir örnek toplayıp her birini ölçebiliriz. Daha sonra popülasyonun ortalama yüksekliğini tahmin etmek için örnekteki bitkilerin ortalama yüksekliğini kullanabiliriz.

Ancak örneğimizin mükemmel bir nüfus tahmini sağlaması pek olası değildir. Neyse ki, bu belirsizliği, gerçek popülasyon parametresinin içinde bulunduğundan emin olduğumuz bir dizi değer sağlayan birgüven aralığı oluşturarak açıklayabiliriz.

Örneğin, [13,2, 14,8] şeklinde %95’lik bir güven aralığı üretebiliriz; bu, bu bitki türünün gerçek ortalama boyunun 13,2 inç ile 14,8 inç arasında olduğundan %95 emin olduğumuz anlamına gelir.

3. Regresyon .

Bazen bir popülasyondaki iki değişken arasındaki ilişkiyi anlamak isteriz.

Örneğin, haftada ders çalışmaya harcanan saatlerin sınav puanlarıyla ilişkili olup olmadığını bilmek istediğimizi varsayalım. Bu soruyu cevaplamak içinregresyon analizi olarak bilinen bir teknik uygulayabiliriz.

Böylece 100 öğrencinin ders saatlerine ve test puanlarına bakabilir ve iki değişken arasında anlamlı bir ilişki olup olmadığını görmek için regresyon analizi yapabiliriz.

Regresyonun p değeri anlamlı bulunursa öğrenci popülasyonunun genelinde bu iki değişken arasında anlamlı bir ilişkinin olduğu sonucuna varabiliriz.

Tanımlayıcı ve çıkarımsal istatistikler arasındaki fark

Özetle, tanımlayıcı ve çıkarımsal istatistikler arasındaki fark şu şekilde açıklanabilir:

Tanımlayıcı istatistikler, bir veri kümesini tanımlamak için özet istatistikleri, grafikleri ve tabloları kullanır.

Bu, tüm bireysel veri değerlerine girmeden bir veri kümesini hızlı ve kolay bir şekilde anlamamıza yardımcı olması açısından faydalıdır.

Çıkarımsal istatistikler, daha büyük popülasyonlar hakkında sonuçlar çıkarmak için örnekleri kullanır.

Bir popülasyon hakkında cevaplamak istediğiniz soruya bağlı olarak aşağıdaki yöntemlerden birini veya birkaçını kullanmaya karar verebilirsiniz: hipotez testi, güven aralıkları ve regresyon analizi.

Bu yöntemlerden birini kullanmayı seçerseniz, örneğinizin popülasyonunuzu temsil etmesi gerektiğini unutmayın, aksi takdirde çıkardığınız sonuçlar güvenilir olmayacaktır.