Tek yönlü anova: tanım, formül ve örnek
Tek yönlü ANOVA (“varyans analizi”), karşılık gelen popülasyonun ortalamaları arasında istatistiksel olarak anlamlı bir fark olup olmadığını belirlemek için üç veya daha fazla bağımsız grubun ortalamalarını karşılaştırır.
Bu eğitimde aşağıdakiler açıklanmaktadır:
- Tek yönlü bir ANOVA gerçekleştirme motivasyonu.
- Tek yönlü ANOVA gerçekleştirmek için karşılanması gereken varsayımlar.
- Tek yönlü ANOVA gerçekleştirme süreci.
- Tek yönlü ANOVA’nın nasıl gerçekleştirileceğine bir örnek.
Tek yönlü ANOVA: motivasyon
Üç farklı sınava hazırlık programının üniversiteye giriş sınavında farklı ortalama puanlara yol açıp açmadığını bilmek istediğimizi varsayalım. Ülke çapında milyonlarca lise öğrencisi olduğundan, her öğrenciyi tek tek dolaşıp sınava hazırlık programlarından birini kullanmalarına izin vermek çok zaman alıcı ve pahalı olacaktır.
Bunun yerine, evrenden 100 öğrenciden oluşan rastgele üç örnek seçebilir ve her örneğin sınava hazırlanmak için üç test hazırlık programından birini kullanmasına izin verebiliriz. Daha sonra sınava girdikten sonra her öğrencinin puanlarını kaydedebiliriz.
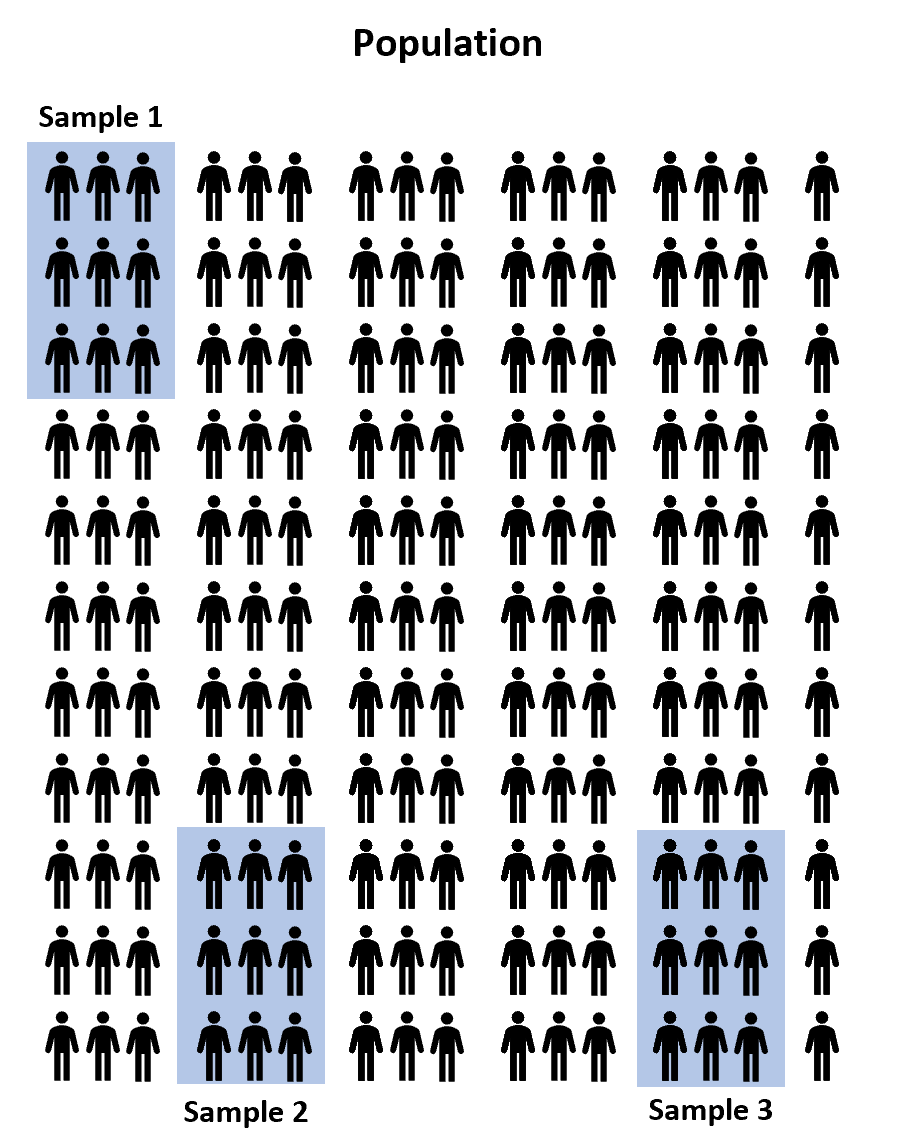
Ancak üç örnek arasındaki ortalama sınav puanının en azından biraz farklı olacağı neredeyse garantidir. Soru, bu farkın istatistiksel olarak anlamlı olup olmadığıdır . Neyse ki tek yönlü ANOVA bu soruyu yanıtlamamıza olanak sağlıyor.
Tek yönlü ANOVA: varsayımlar
Tek yönlü ANOVA sonuçlarının geçerli olabilmesi için aşağıdaki varsayımların karşılanması gerekir:
1. Normallik – Her örnek normal dağılmış bir popülasyondan alınmıştır.
2. Eşit varyanslar – Örneklerin alındığı popülasyonların varyansları eşittir. Bu hipotezi test etmek için Bartlett testini kullanabilirsiniz.
3. Bağımsızlık – Her grup içindeki gözlemler birbirinden bağımsızdır ve gruplar içindeki gözlemler rastgele örnekleme yoluyla elde edilmiştir.
Bu varsayımların nasıl doğrulanacağına ilişkin daha fazla ayrıntı için bu makaleyi okuyun.
Tek yönlü ANOVA: süreç
Tek yönlü bir ANOVA aşağıdaki boş ve alternatif hipotezleri kullanır:
- H 0 (sıfır hipotezi): μ 1 = μ 2 = μ 3 = … = μ k (tüm popülasyon ortalamaları eşittir)
- H 1 (alternatif hipotez): en az bir popülasyon ortalaması farklıdır dinlenmek
Tek yönlü ANOVA’yı manuel olarak gerçekleştirmek sıkıcı olduğundan, genellikle bazı istatistiksel yazılımları (R, Excel, Stata, SPSS vb.) kullanırsınız.
Kullandığınız yazılımdan bağımsız olarak çıktı olarak aşağıdaki tabloyu alacaksınız:
| Kaynak | Kareler toplamı (SS) | df | Ortalama kareler (MS) | F | P |
|---|---|---|---|---|---|
| Tedavi | RSS | df r | MSR | MSR/MSE | F df r , df e |
| Hata | ESS | df e | MSE | ||
| Toplam | İSG | df t |
Altın:
- SSR: kareler toplamı regresyonu
- SSE: karesel hatanın toplamı
- SST: toplam kareler toplamı (SST = SSR + SSE)
- df r : regresyon serbestlik dereceleri (df r = k-1)
- df e : hata serbestlik derecesi (df e = nk)
- df t : toplam serbestlik derecesi (sd t = n-1)
- k: toplam grup sayısı
- n: toplam gözlemler
- MSR: ortalama kare regresyon (MSR = SSR/df r )
- MSE: ortalama kare hatası (MSE = SSE/df e )
- F: F testi istatistiği (F = MSR/MSE)
- p: F dfr, dfe’ye karşılık gelen p değeri
P değeri seçilen anlamlılık seviyesinden (örneğin 0,05) küçükse, boş hipotezi reddedebilir ve popülasyon ortalamalarından en az birinin diğerlerinden farklı olduğu sonucuna varabilirsiniz.
Not: Sıfır hipotezini reddederseniz, bu, popülasyon ortalamalarından en az birinin diğerlerinden farklı olduğunu gösterir, ancak ANOVA tablosu hangi popülasyon ortalamalarının farklı olduğunu belirtmez. Bunu belirlemek için “çoklu karşılaştırma” testi olarak da adlandırılan post hoc testi yapmanız gerekir.
Tek yönlü ANOVA: örnek
Üç farklı sınava hazırlık programının belirli bir sınavda farklı ortalama puanlara yol açıp açmadığını bilmek istediğimizi varsayalım. Bunu test etmek için 30 öğrenciyi bir çalışmaya katıyoruz ve onları üç gruba ayırıyoruz.
Her gruptaki öğrenciler, bir sınava hazırlanmak için sonraki üç hafta boyunca üç sınav hazırlık programından birini kullanmak üzere rastgele atanır . Üç haftanın sonunda tüm öğrenciler aynı sınava girerler.
Her gruba ait sınav sonuçları aşağıda gösterilmektedir:
Bu veriler üzerinde tek yönlü ANOVA gerçekleştirmek için İstatistik Tek Yönlü ANOVA Hesaplayıcısını aşağıdaki girdiyle kullanacağız:
Çıktı tablosundan F testi istatistiğinin 2,358 ve buna karşılık gelen p değerinin 0,11385 olduğunu görüyoruz.
Bu p değeri 0,05’ten küçük olmadığından sıfır hipotezini reddedemiyoruz.
Bu , üç grubun ortalama sınav puanları arasında istatistiksel olarak anlamlı bir fark olduğunu söyleyecek yeterli kanıta sahip olmadığımız anlamına geliyor .
Ek kaynaklar
Aşağıdaki makaleler, farklı istatistiksel yazılımlar kullanılarak tek yönlü ANOVA’nın nasıl gerçekleştirileceğini açıklamaktadır:
Excel’de Tek Yönlü ANOVA Nasıl Gerçekleştirilir
R’de tek yönlü ANOVA nasıl gerçekleştirilir
Python’da Tek Yönlü ANOVA Nasıl Gerçekleştirilir
SAS’ta tek yönlü ANOVA nasıl gerçekleştirilir?
SPSS’de Tek Yönlü ANOVA Nasıl Gerçekleştirilir
Stata’da tek yönlü ANOVA nasıl gerçekleştirilir?
TI-84 Hesap Makinesinde Tek Yönlü ANOVA Nasıl Gerçekleştirilir
Çevrimiçi Tek Yönlü ANOVA Hesaplayıcı
yazar hakkında
Dr.benjamin anderson
Merhaba, ben Benjamin, emekli bir istatistik profesörü ve Statorials öğretmenine dönüştüm. İstatistik alanındaki kapsamlı deneyimim ve uzmanlığımla, öğrencilerimi Statorials aracılığıyla güçlendirmek için bilgilerimi paylaşmaya can atıyorum. Daha fazlasını bil