Excel'de tek yönlü anova nasıl gerçekleştirilir

Üç veya daha fazla bağımsız grubun ortalamaları arasında istatistiksel olarak anlamlı bir fark olup olmadığını belirlemek için tek yönlü ANOVA (“varyans analizi”) kullanılır.

Bu eğitimde Excel’de tek yönlü ANOVA’nın nasıl gerçekleştirileceği açıklanmaktadır.

Örnek: Excel’de Tek Yönlü ANOVA

Bir araştırmacının bir çalışmaya katılmak üzere 30 öğrenciyi işe aldığını varsayalım. Öğrenciler, bir sınava hazırlanmak için önümüzdeki üç hafta boyunca üç çalışma tekniğinden birini kullanmak üzere rastgele atanır. Üç haftanın sonunda tüm öğrenciler aynı sınava girerler.

Öğrenci test sonuçları aşağıda gösterilmektedir:

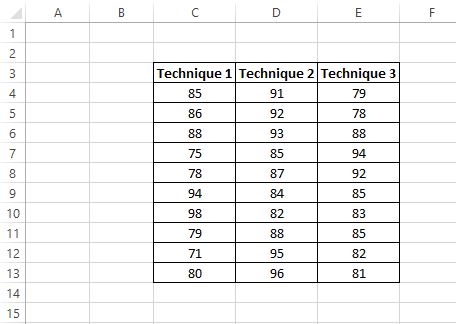
Araştırmacı, ortalama puanların üç grup arasında aynı olup olmadığını belirlemek için tek yönlü bir ANOVA gerçekleştirmek istiyor.

Excel’de tek yönlü ANOVA gerçekleştirmek için Veri sekmesine gidin ve ardından Analiz grubundaki Veri Analizi seçeneğine tıklayın.

Veri Analizi seçeneğini göremiyorsanız , öncelikle ücretsiz Analiz Araç Paketi yazılımını yüklemelisiniz .

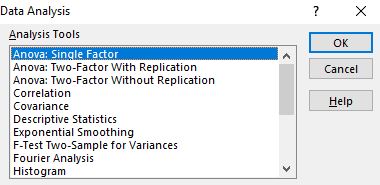
Üzerine tıkladığınızda, farklı tarama aracı seçeneklerinin bulunduğu bir pencere açılacaktır. Anova: Tek Faktör’ü seçin ve ardından Tamam’a tıklayın.

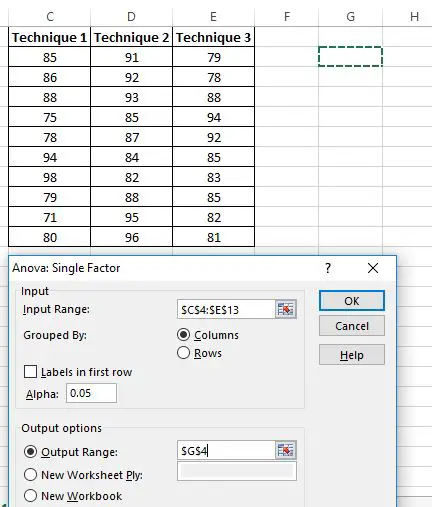
Giriş aralığını soran yeni bir pencere açılır. Verilerinizin etrafına bir kutu sürükleyebilir veya veri aralığını manuel olarak girebilirsiniz. Bu durumda verilerimiz C4:E13 hücrelerindedir.

Daha sonra test için bir Alfa düzeyi seçin. Varsayılan olarak bu sayı 0,05’tir. Bu durumda 0,05’te bırakacağım.

Son olarak, tek yönlü ANOVA sonuçlarının görüneceği Çıkış Aralığı için bir hücre seçin. Bu durumda G4 hücresini seçiyorum.

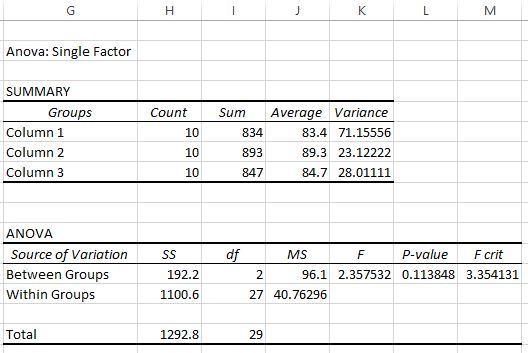
Tamam’a tıkladığınızda tek yönlü ANOVA sonucu görünecektir:

Sonucun yorumlanması

Çıktıda iki tablo görüntülenir. Birincisi, her gruptaki test puanlarının sayısını, test puanlarının toplamını, test puanlarının ortalamasını ve test puanlarının varyansını gösteren bir özet tablodur.

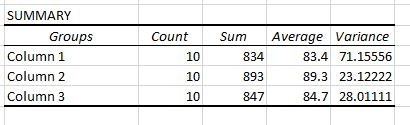
Üç veya daha fazla grubun ortalamaları arasında istatistiksel olarak anlamlı bir fark olup olmadığını belirlemek için tek yönlü ANOVA’nın kullanıldığını hatırlayın.

Bu ilk tablodan üç grubun her birinin ortalama puanının farklı olduğunu görebiliriz ancak bu farklılıkların istatistiksel olarak anlamlı olup olmadığını bilmek için ikinci tabloya bakmamız gerekir.

İkinci tablo F testi istatistiğini, kritik F değerini ve p değerini gösterir:

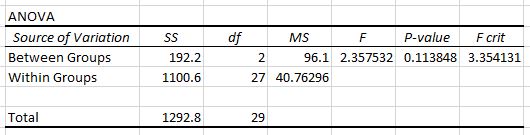
Bu durumda F test istatistiği 2,3575 ve F’nin kritik değeri 3,3541 olur. F testi istatistiği, F’nin kritik değerinden küçük olduğundan, üç grubun ortalamalarının eşit olduğunu belirten sıfır hipotezini reddetmek için yeterli kanıtımız yok.

Bu, üç çalışma tekniği arasında test sonuçlarında farklılık olduğunu söylemek için yeterli kanıta sahip olmadığımız anlamına gelir.

Aynı sonuca ulaşmak için p değerini de kullanabiliriz. Bu durumda p değeri 0,1138 olup alfa düzeyi olan 0,05’ten yüksektir.

Bu, üç grubun ortalamalarının eşit olduğunu belirten sıfır hipotezini reddetmek için yeterli kanıtımız olmadığı anlamına gelir.

Not: Sıfır hipotezini reddettiğiniz durumlarda, tam olarak hangi grup ortalamalarının farklı olduğunu belirlemek için bir Tukey-Kramer post hoc testi gerçekleştirebilirsiniz.