Spss'de tek yönlü anova nasıl gerçekleştirilir

Üç veya daha fazla bağımsız grubun ortalamaları arasında istatistiksel olarak anlamlı bir fark olup olmadığını belirlemek için tek yönlü ANOVA kullanılır.

Bu tür testlere tek yönlü ANOVA denir çünkü bir yordayıcı değişkenin bir yanıt değişkeni üzerindeki etkisini analiz ederiz.

Bunun yerine iki öngörücü değişkenin bir yanıt değişkeni üzerindeki etkisiyle ilgilenseydik, iki yönlü bir ANOVA gerçekleştirebilirdik.

Bu eğitimde SPSS’de tek yönlü ANOVA’nın nasıl gerçekleştirileceği açıklanmaktadır.

Örnek: SPSS’de Tek Yönlü ANOVA

Bir araştırmacının bir çalışmaya katılmak üzere 30 öğrenciyi işe aldığını varsayalım. Öğrenciler bir sonraki ay sınava hazırlanmak için üç çalışma tekniğinden birini kullanmak üzere rastgele atanır. Ay sonunda tüm öğrenciler aynı sınava girerler.

Öğrenci test sonuçları aşağıda gösterilmektedir:

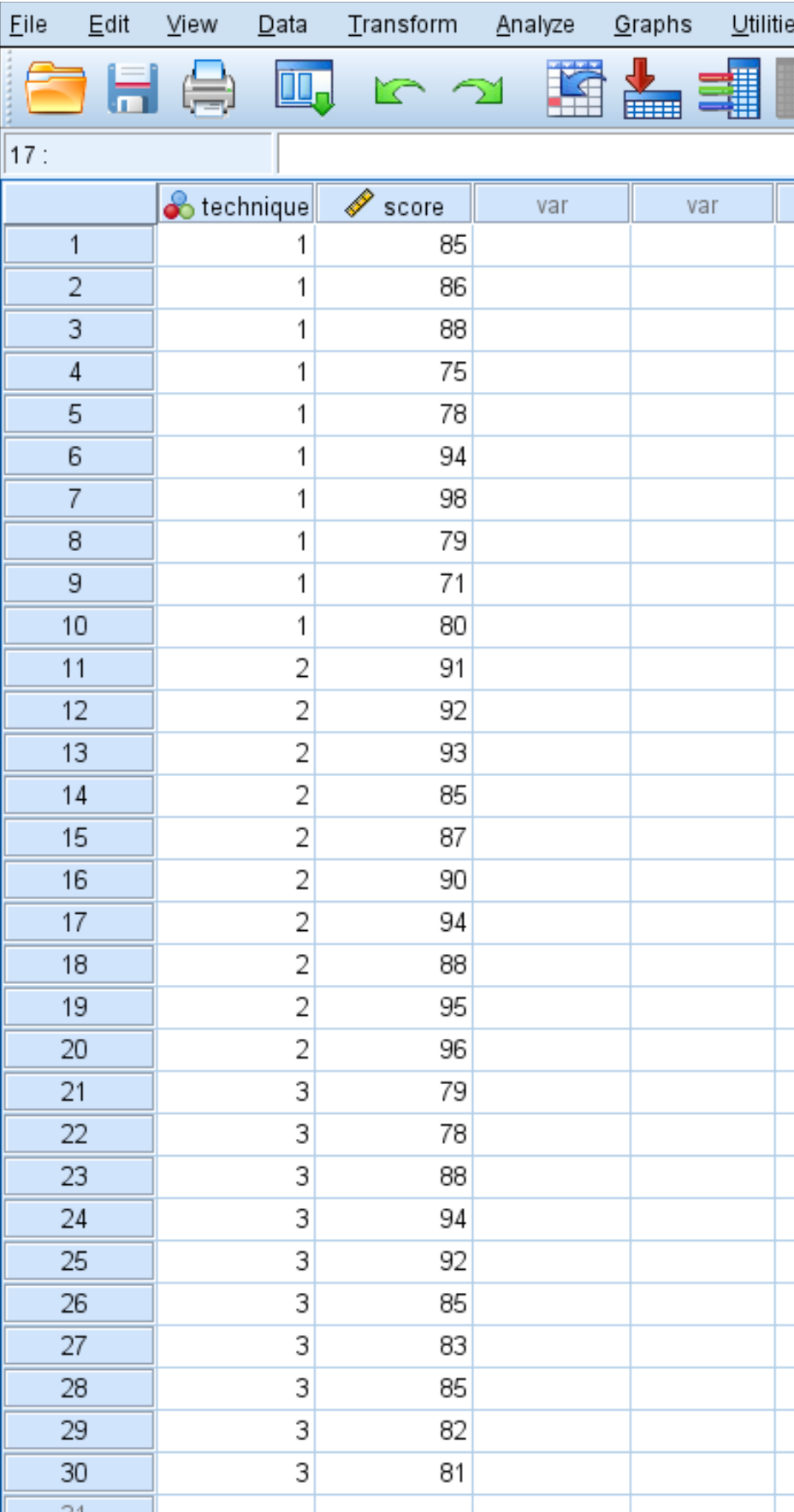
Ortalama puanların üç grup arasında aynı olup olmadığını belirlemek amacıyla tek yönlü bir ANOVA gerçekleştirmek için aşağıdaki adımları kullanın.

Adım 1: Verileri görselleştirin.

İlk olarak, üç çalışma tekniğinin her biri için test puanlarının dağılımını görselleştirmek amacıyla kutu grafikleri oluşturacağız. Grafikler sekmesini ve ardından Grafik Oluşturucu’yu tıklayın.

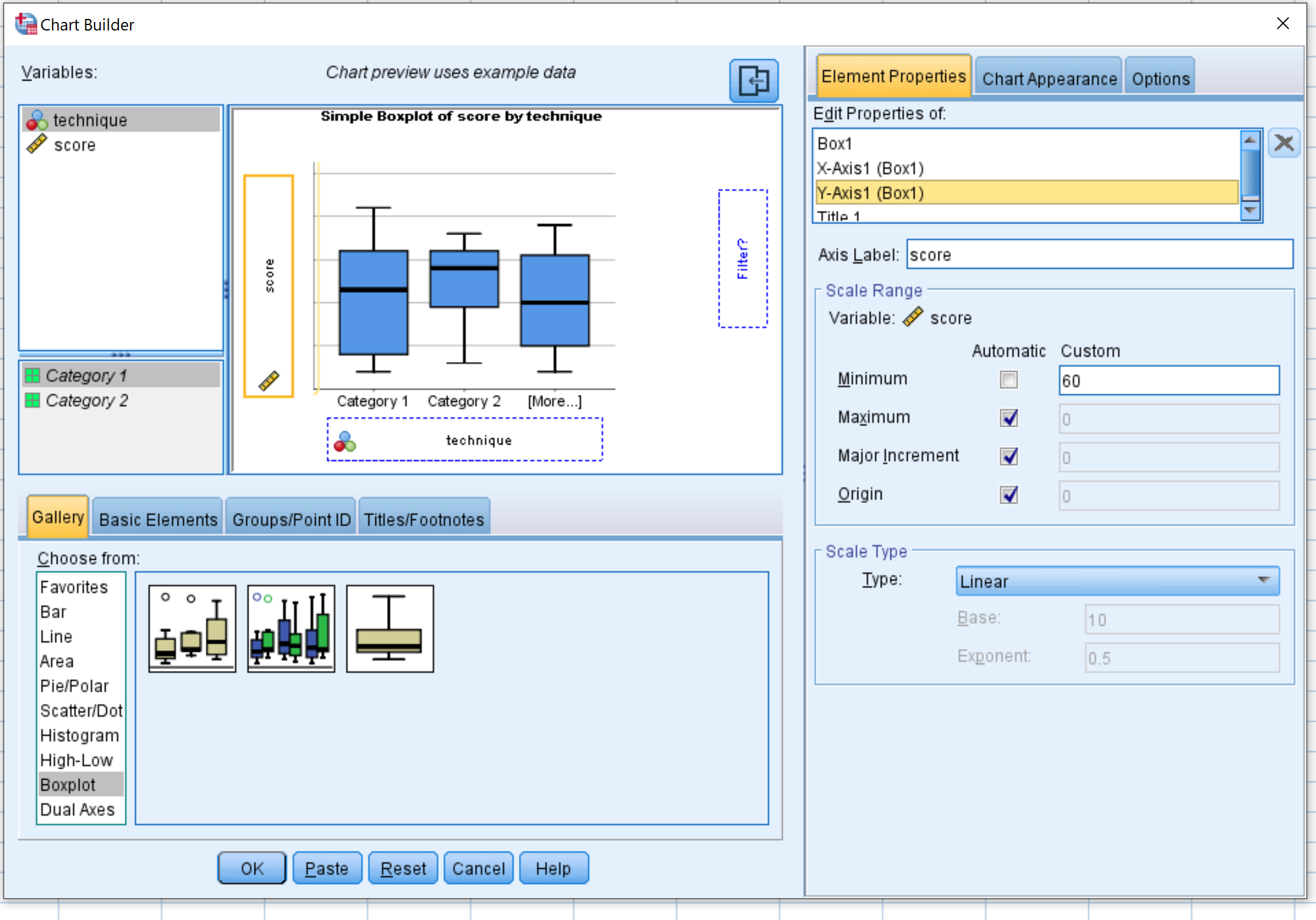
Şuradan seç: penceresinde Kutu grafiği’ni seçin. Daha sonra Basit kutu grafiği etiketli ilk grafiği ana düzenleme penceresine sürükleyin. Teknik değişkeni x eksenine ve puanı da y eksenine sürükleyin.

Daha sonra Eleman Özellikleri’ni ve ardından Y1 Ekseni’ni tıklayın. Minimum değeri 60 olarak değiştirin. Ardından Tamam’a tıklayın.

Aşağıdaki kutu grafikleri görünecektir:

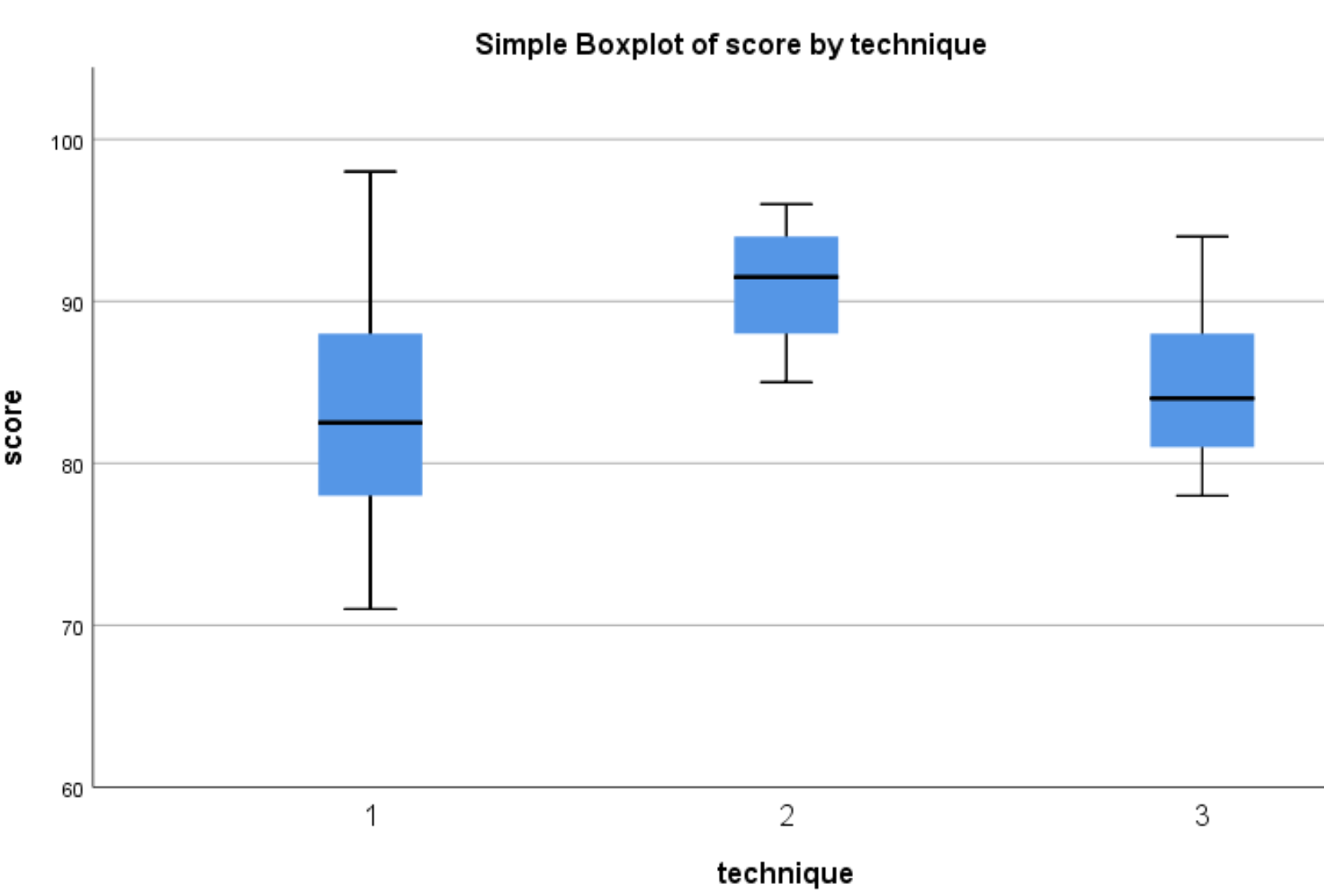
Test puanlarının dağılımının, Teknik 2’yi kullanan öğrenciler için, Teknik 1 ve 3’ü kullanan öğrencilere göre daha yüksek olma eğiliminde olduğunu görebiliriz. Bu puan farklılıklarının istatistiksel olarak anlamlı olup olmadığını belirlemek için tek yönlü bir ANOVA gerçekleştireceğiz.

Adım 2: Tek yönlü ANOVA gerçekleştirin.

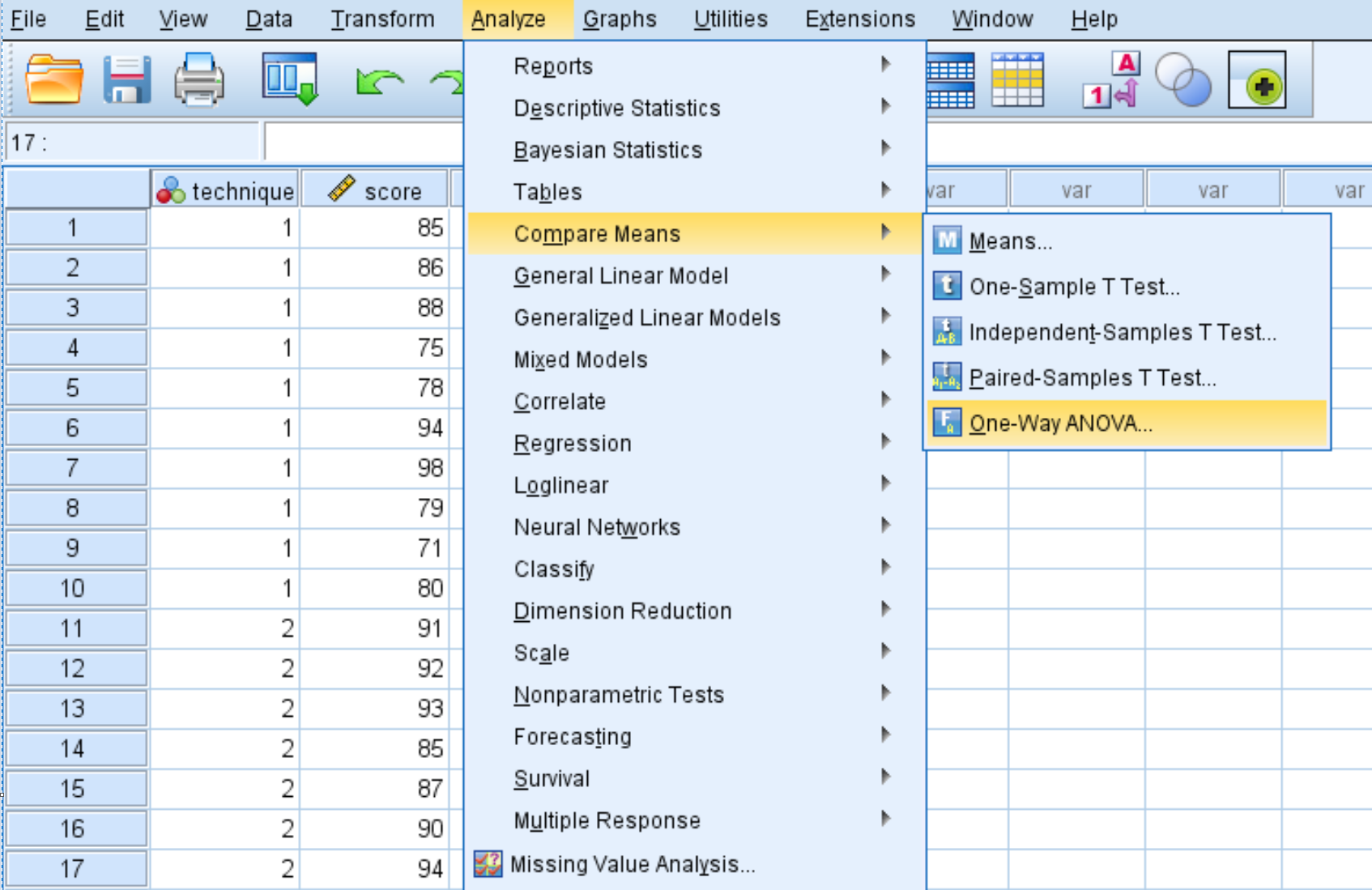
Analiz sekmesine, ardından Ortalamaları Karşılaştır’a ve ardından Tek Yönlü ANOVA’ya tıklayın.

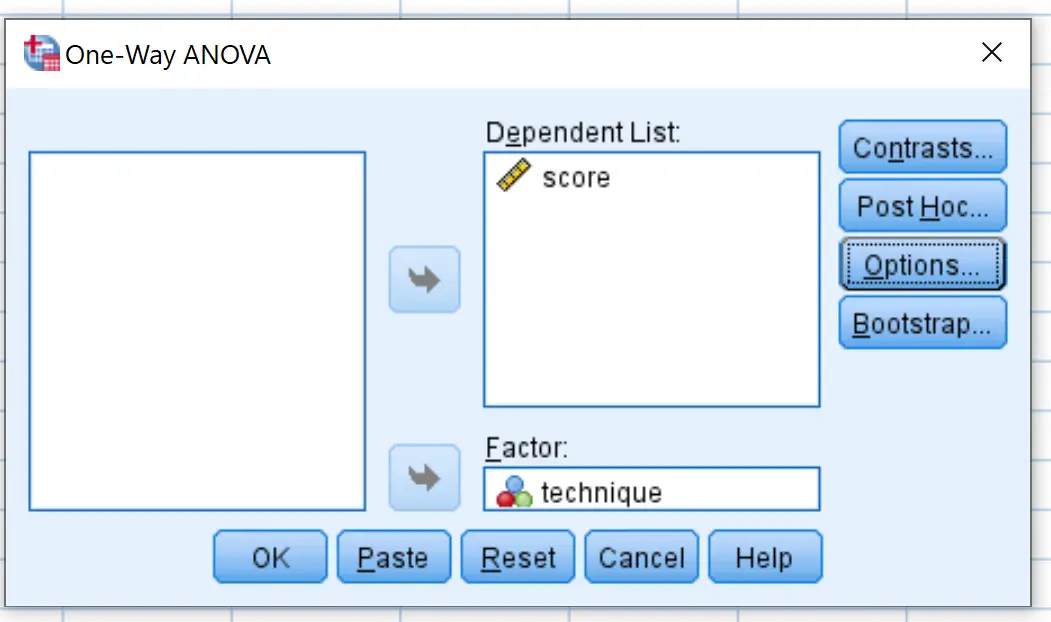
Açılan yeni pencerede, değişken puanını Bağımlı Liste etiketli kutuya ve değişken tekniğini Faktör etiketli kutuya yerleştirin.

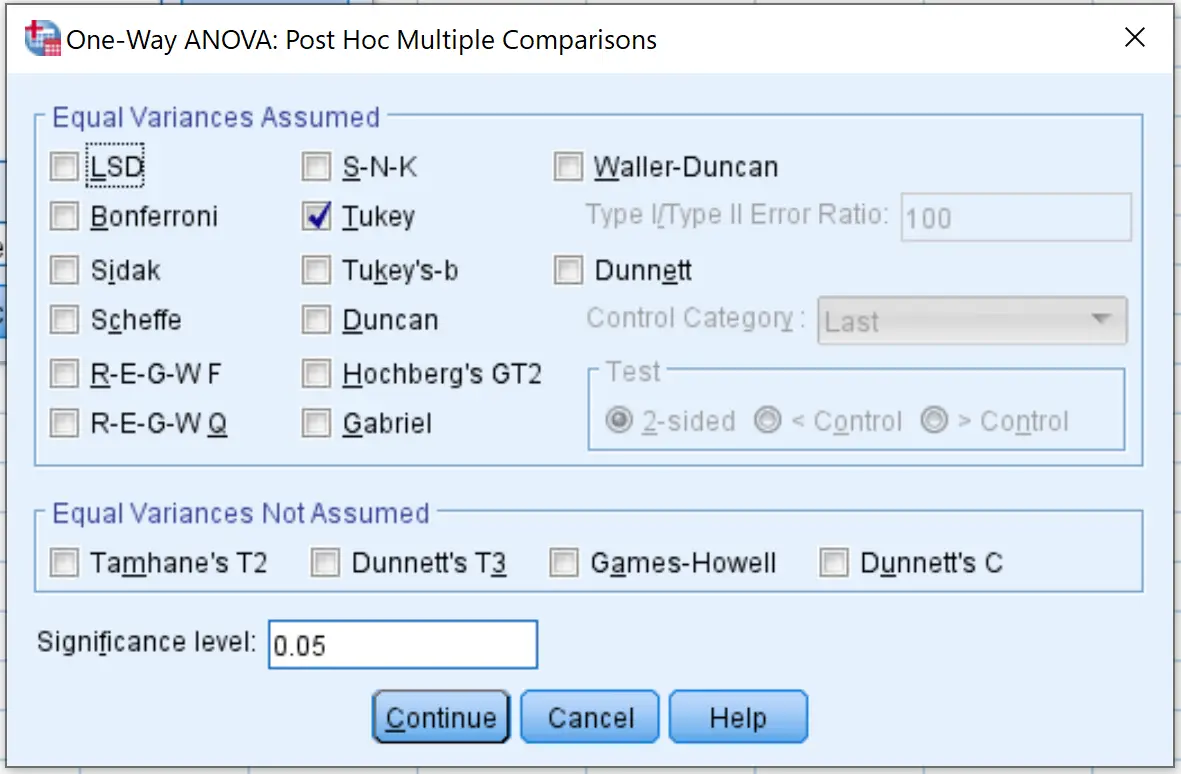
Ardından Post Hoc’a tıklayın ve Tukey’in yanındaki kutuyu işaretleyin. Daha sonra Devam’ı tıklayın.

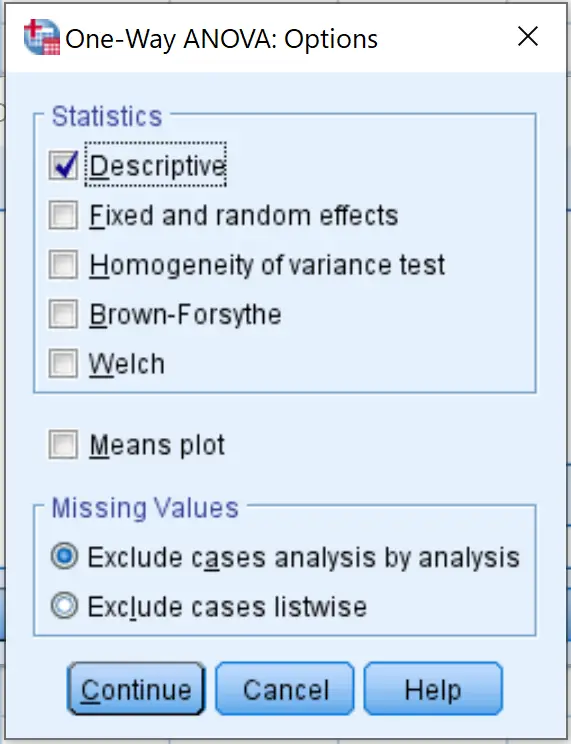
Ardından Seçenekler’i tıklayın ve Açıklayıcı’nın yanındaki kutuyu işaretleyin. Daha sonra Devam’ı tıklayın.

Son olarak Tamam’ı tıklayın.

Adım 3: Sonucu yorumlayın.

Tamam’a tıkladığınızda tek yönlü ANOVA sonuçları görünecektir. Sonucun nasıl yorumlanacağı aşağıda açıklanmıştır:

Tablo açıklaması

Bu tablo, veri setimizdeki üç grubun her biri için tanımlayıcı istatistikleri görüntüler.

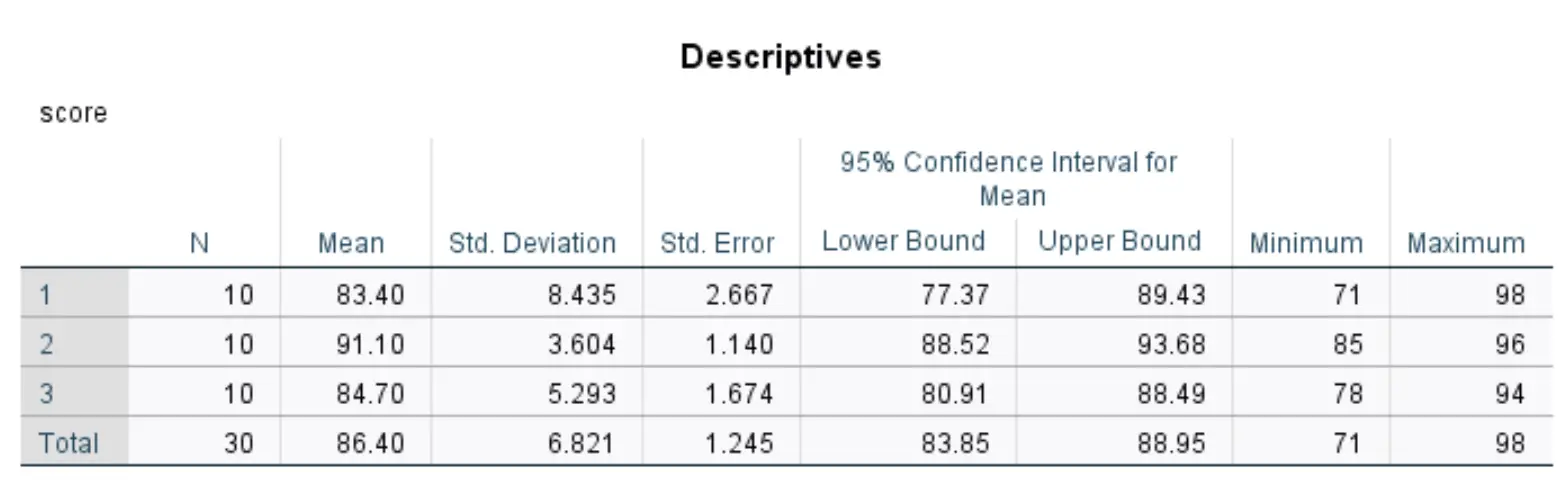
En alakalı rakamlar şunları içerir:

• N: Her gruptaki öğrenci sayısı.
• Ortalama: Her grup için ortalama test puanı.
• Standart. Sapma: Her grup için test sonuçlarının standart sapması.

ANOVA tablosu

Bu tablo tek yönlü ANOVA’nın sonuçlarını görüntüler:

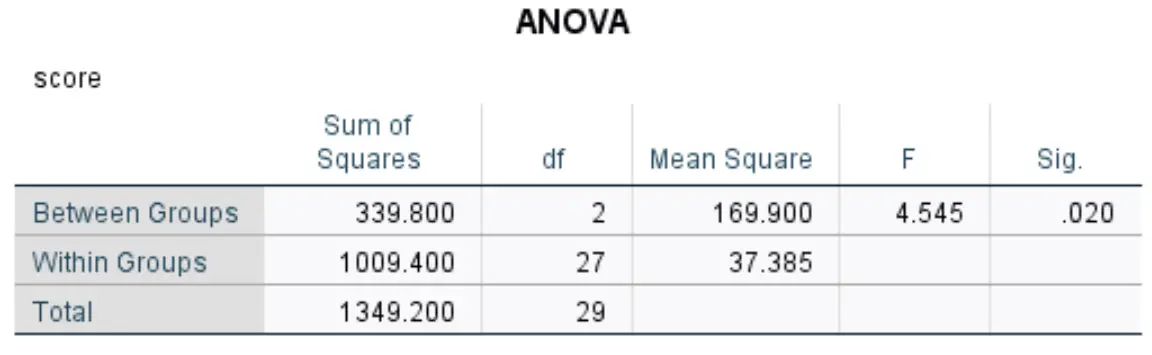
En alakalı rakamlar şunları içerir:

• F: Genel F istatistiği.
• Sig: Pay df (2) ve payda df (27) ile F istatistiğine (4,545) karşılık gelen p değeri. Bu durumda p değeri 0,020 olur.

Tek yönlü bir ANOVA’nın aşağıdaki boş ve alternatif hipotezleri kullandığını hatırlayın:

• H ₀ (sıfır hipotezi): μ ₁ = μ ₂ = μ ₃ = … = μ _k (tüm popülasyon ortalamaları eşittir)
• H _A (alternatif hipotez): en az bir popülasyon ortalaması farklıdır   dinlenmek

ANOVA tablosunun p değeri 0,05’ten küçük olduğundan, sıfır hipotezini reddetmek ve grup ortalamalarından en az birinin diğerlerinden farklı olduğu sonucuna varmak için yeterli kanıtımız var.

Hangi grup ortalamalarının birbirinden farklı olduğunu tam olarak bilmek için ANOVA sonucunun son tablosuna bakabiliriz.

Çoklu karşılaştırma tablosu

Bu tablo, Tukey’in üç grubun her biri arasındaki post-hoc çoklu karşılaştırmalarını gösterir. Biz esas olarak Sig ile ilgileniyoruz. Her grup arasındaki ortalama farklar için p değerlerini görüntüleyen sütun:

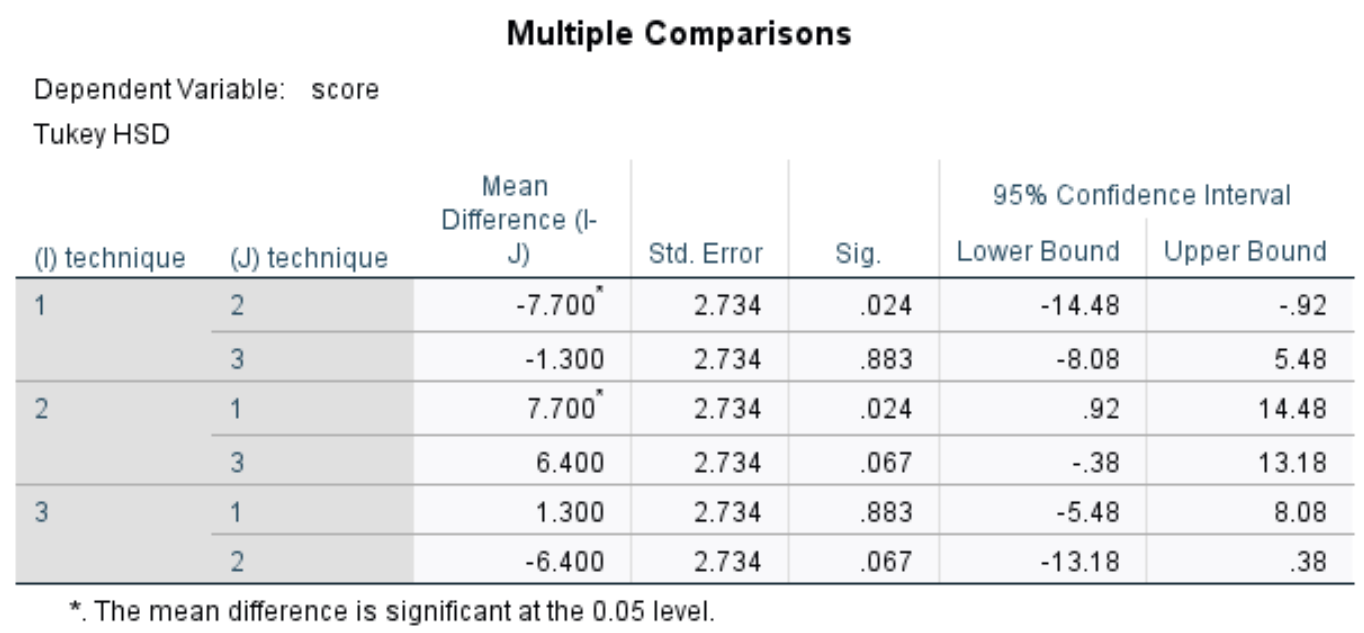
Tabloda aşağıdaki karşılaştırmalar için p değerlerini görebiliriz:

• Teknik 1’e karşı 2: | p-değeri = 0,024
• Teknik 1’e karşı 3 | p-değeri = 0,883
• Teknik 2’ye karşı 3 | p-değeri = 0,067

P değeri 0,05’in altında olan tek grup karşılaştırması Teknik 1 ile Teknik 2 arasındadır.

Bu bize, Teknik 1’i kullanan öğrenciler ile Teknik 2’yi kullanan öğrenciler arasında ortalama test puanları arasında istatistiksel olarak anlamlı bir fark olduğunu göstermektedir.

Ancak teknik 1 ile 3 arasında veya teknik 2 ile 3 arasında istatistiksel olarak anlamlı bir fark yoktur.

Adım 4: Sonuçları rapor edin.

Son olarak tek yönlü ANOVA sonuçlarını raporlayabiliriz. İşte bunun nasıl yapılacağına dair bir örnek:

Üç farklı çalışma tekniğinin farklı test sonuçlarına yol açıp açmadığını belirlemek için tek yönlü bir ANOVA yapıldı.

Toplam 10 öğrenci aynı teste girmeden önce bir ay boyunca üç çalışma tekniğinin her birini kullandı.

Tek yönlü ANOVA, en az iki grup arasında test puanlarında istatistiksel olarak anlamlı bir fark olduğunu ortaya çıkardı (F(2, 27) = 4,545, p = 0,020).

Tukey’in çoklu karşılaştırma testi, Teknik 1 ve Teknik 2’yi kullanan öğrenciler arasında ortalama test puanlarının anlamlı düzeyde farklı olduğunu ortaya çıkardı (p = 0,024, %95 GA = [-14,48, -0,92]).

Teknik 1 ve 3 puanları arasında (p = 0,883) veya teknik 2 ve 3 puanları arasında (p = 0,067) istatistiksel olarak anlamlı bir fark yoktu.