Sas'ta tek yönlü anova nasıl gerçekleştirilir?

Üç veya daha fazla bağımsız grubun ortalamaları arasında istatistiksel olarak anlamlı bir fark olup olmadığını belirlemek için tek yönlü ANOVA kullanılır.

Bu eğitimde, SAS’ta tek yönlü ANOVA’nın nasıl gerçekleştirileceğine ilişkin adım adım bir örnek sunulmaktadır.

1. Adım: Verileri oluşturun

Bir araştırmacının bir çalışmaya katılmak üzere 30 öğrenciyi işe aldığını varsayalım. Öğrenciler bir sınava hazırlanmak için üç çalışma yönteminden birini kullanmak üzere rastgele atanır .

Her öğrencinin sınav sonuçları aşağıda gösterilmektedir:

Bu veri kümesini SAS’ta oluşturmak için aşağıdaki kodu kullanabiliriz:

 /*create dataset*/
data my_data;
    input Method $Score;
    datalines ;
At 78
At 81
At 82
At 82
At 85
At 88
At 88
At 90
B 81
B 83
B 83
B85
B 86
B 88
B90
B91
C 84
C 88
C 88
C 89
C 90
C 93
C 95
C 98
;
run ;

Adım 2: Tek Yönlü ANOVA gerçekleştirin

Daha sonra tek yönlü ANOVA’yı gerçekleştirmek için proc ANOVA’yı kullanacağız:

 /*perform one-way ANOVA*/
proc ANOVA data =my_data;
classMethod ;
modelScore = Method;
means Method / tukey cldiff ;
run ;

Not : Tek yönlü ANOVA’dan elde edilen genel p değeri istatistiksel olarak anlamlıysa Tukey post-hoc testinin yapılması gerektiğini belirtmek için ortalama fonksiyonunu kullandık.

3. Adım: Sonuçları yorumlayın

Sonuçlarda analiz etmek istediğimiz ilk tablo ANOVA tablosudur:

Bu tablodan şunları görebiliriz:

• Genel F değeri: 5,26
• Karşılık gelen p değeri: 0,0140

Tek yönlü bir ANOVA’nın aşağıdaki boş ve alternatif hipotezleri kullandığını hatırlayın:

• H ₀ : Tüm grup ortalamaları eşittir.
• H _A : En az bir grubun ortalaması farklı   dinlenmek.

ANOVA tablosunun p değeri (0,0140) α = 0,05’ten küçük olduğundan sıfır hipotezini reddediyoruz.

Bu bize ortalama sınav puanının üç çalışma yöntemi arasında eşit olmadığını söyler.

İlgili: ANOVA’da F-Değeri ve P-Değeri Nasıl Yorumlanır?

SAS ayrıca üç çalışma yönteminin her biri için sınav sonuçlarının dağılımını görselleştirmek için kutu grafikleri sağlar:

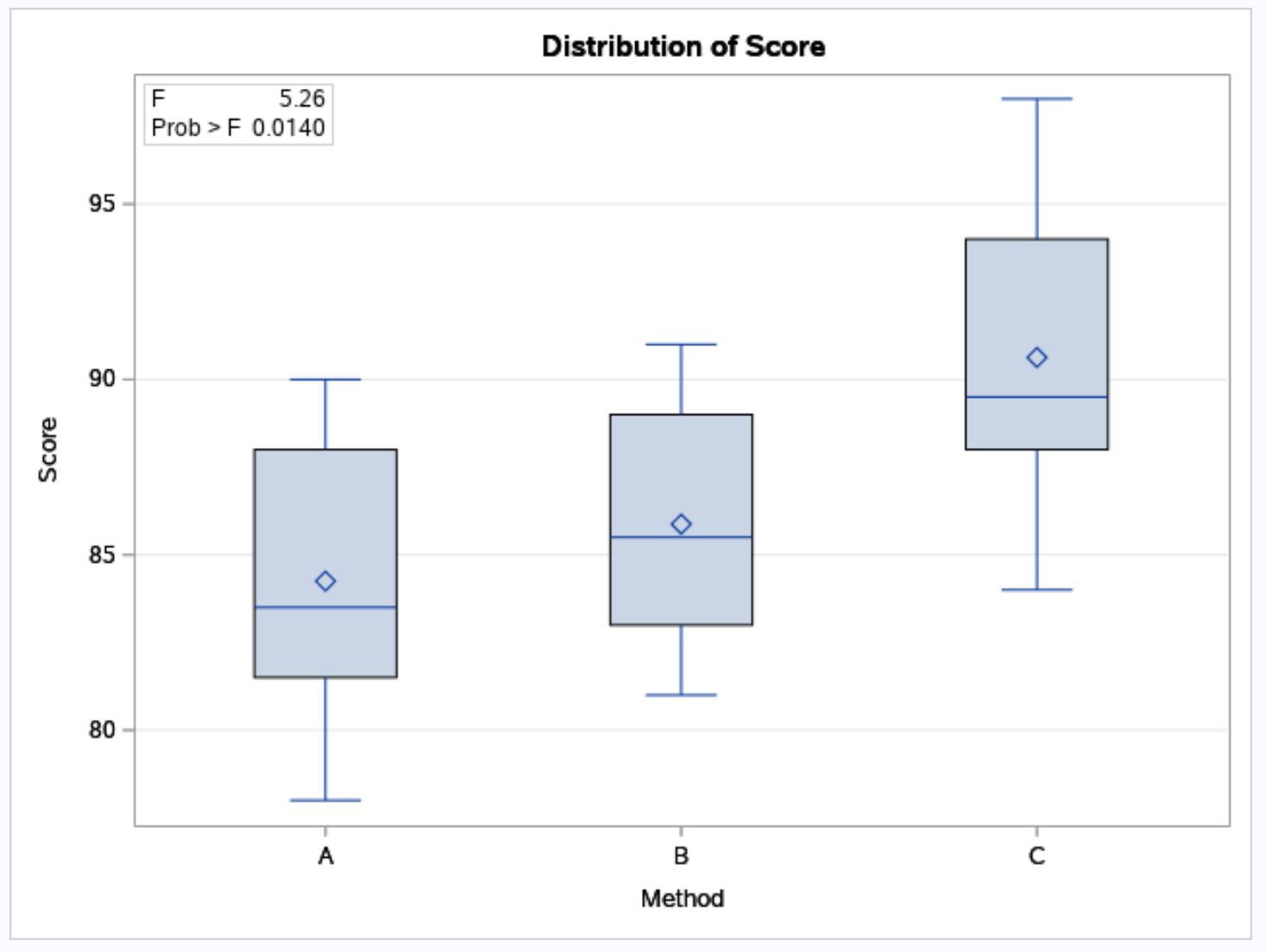
Kutu çizimlerinden sınav puanlarının, çalışma yöntemi C’yi kullanan öğrenciler arasında B ve C yöntemlerine kıyasla daha yüksek olma eğiliminde olduğunu görebiliriz.

Tam olarak hangi grup ortalamalarının farklı olduğunu belirlemek için Tukey’in post-hoc testlerinin sonuçlarını gösteren nihai sonuç tablosuna bakmamız gerekir:

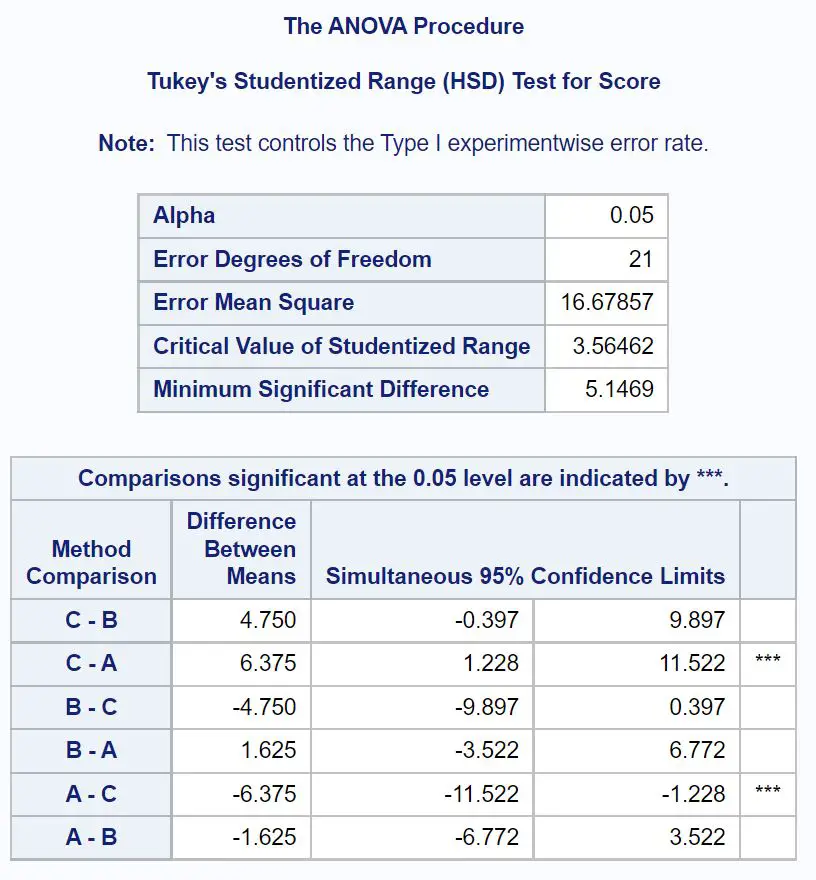
Hangi grup ortalamalarının farklı olduğunu bulmak için hangi ikili karşılaştırmaların yanında yıldız ( *** ) olduğuna bakmamız gerekir.

Tablo, A ve C gruplarının ortalama değerlerinin istatistiksel olarak anlamlı derecede farklı olduğunu göstermektedir.

A ve C grupları arasındaki ortalama sınav puanları farkına ilişkin %95 güven aralığını da görebiliriz:

Ortalama fark için %95 güven aralığı: [1,228, 11,522]

Adım 4: Sonuçları Rapor Edin

Son olarak tek yönlü ANOVA’nın sonuçlarını şu şekilde raporlayabiliriz :

Üç farklı çalışma yönteminin inceleme sonuçları üzerindeki etkisini karşılaştırmak için tek yönlü bir ANOVA yapıldı.

Tek yönlü ANOVA, en az iki grup arasında ortalama sınav puanında istatistiksel olarak anlamlı bir fark olduğunu ortaya çıkardı (F(2,21) = [5,26], p = 0,014).

Çoklu karşılaştırmalara yönelik Tukey HSD testi, sınav puanının ortalama değerinin Yöntem C ve Yöntem A arasında anlamlı düzeyde farklı olduğunu ortaya çıkardı (%95 GA = [1,228, 11,522]).

Yöntem A ile Yöntem B arasında veya Yöntem B ile Yöntem C arasında ortalama sınav puanları arasında istatistiksel olarak anlamlı bir fark yoktu.

Ek kaynaklar

Aşağıdaki eğitimler tek yönlü ANOVA’lar hakkında ek bilgi sağlar:

Tek Yönlü ANOVA’ya Giriş
Tek yönlü ANOVA hesaplayıcı
Tek yönlü ANOVA manuel olarak nasıl gerçekleştirilir?