Tek yönlü veya iki yönlü anova: ne zaman kullanılmalı?

“Varyans Analizi”nin kısaltması olan ANOVA , üç veya daha fazla bağımsız grubun ortalamaları arasında istatistiksel olarak anlamlı bir fark olup olmadığını belirlemek için kullanılır.

ANOVA’nın en yaygın iki türü tek yönlü ANOVA ve iki yönlü ANOVA’dır.

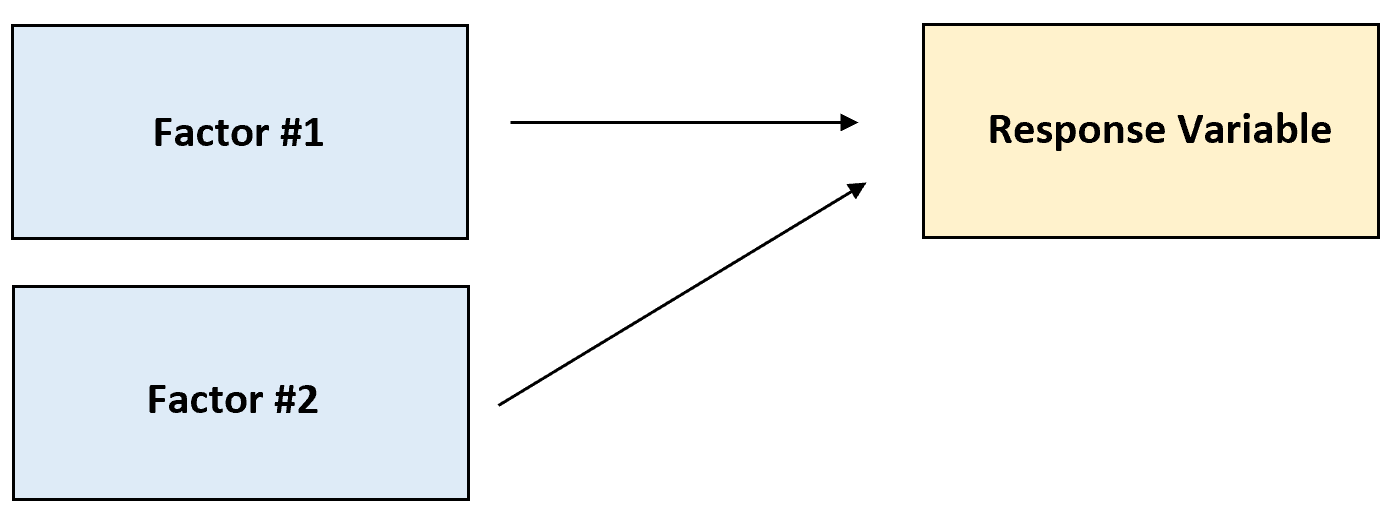
Tek yönlü ANOVA: Bir faktörün yanıt değişkenini nasıl etkilediğini belirlemek için kullanılır.

İki yönlü ANOVA: İki faktörün bir yanıt değişkenini nasıl etkilediğini belirlemek ve yanıt değişkeni üzerinde iki faktör arasında bir etkileşim olup olmadığını belirlemek için kullanılır.

Aşağıdaki örnekler, her ANOVA türünün nasıl gerçekleştirileceğine ilişkin bir örnek sağlar.

Örnek: Tek yönlü ANOVA

Bir profesörün üç farklı çalışma tekniğinin farklı test puanlarına yol açıp açmadığını bilmek istediğini varsayalım. Bunu test etmek için 30 öğrenciyi bir çalışmaya katıyor ve her birinden rastgele bir sınava hazırlanmak için üç teknikten birini kullanmalarını istiyor. Bir ay sonra tüm öğrenciler aynı sınava girer.

Her öğrencinin test sonuçları aşağıda gösterilmektedir:

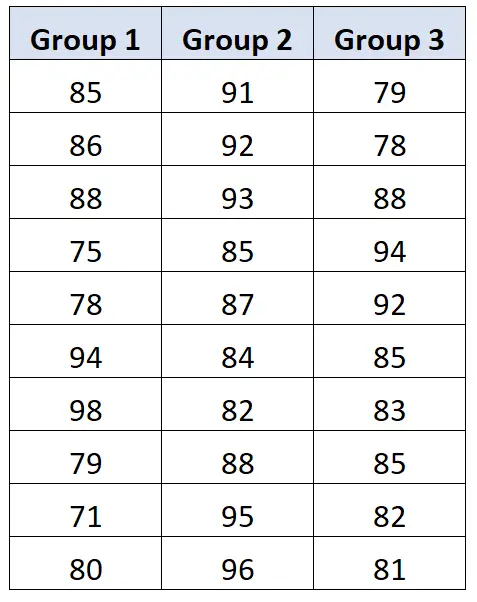
Profesör tek yönlü bir ANOVA gerçekleştirir ve aşağıdaki sonuçları elde eder:

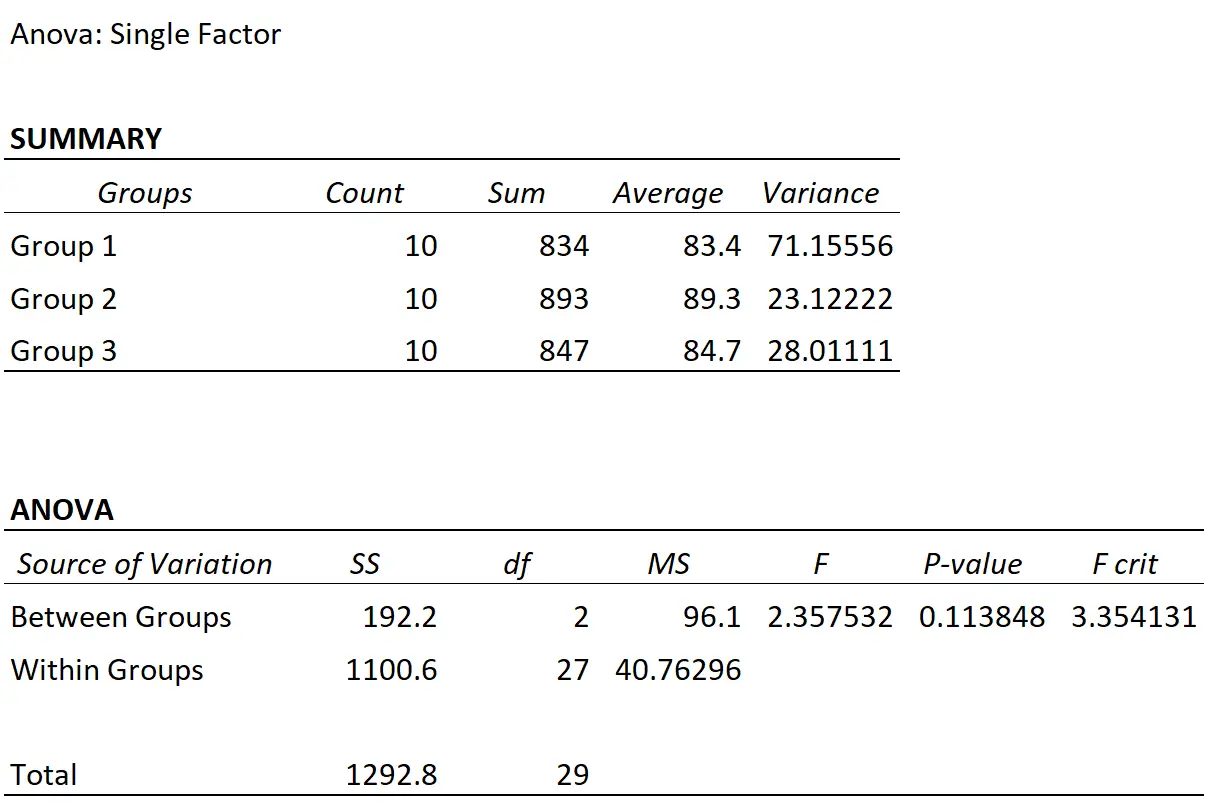
F testi istatistiği 2,3575’tir ve karşılık gelen p değeri 0,1138’dir . Bu p değeri 0,05’ten az olmadığından, üç çalışma tekniğinin farklı ortalama sınav puanlarına yol açtığını söyleyecek yeterli kanıtımız yok.

Örnek: İki yönlü ANOVA

Bir botanikçinin bitki büyümesinin güneş ışığına maruz kalma ve sulama sıklığından etkilenip etkilenmediğini bilmek istediğini varsayalım. 40 tohum ekiyor ve iki ay boyunca farklı güneş ışığı koşullarında ve sulama sıklığında büyümelerini sağlıyor. İki ay sonra her bitkinin yüksekliğini kaydediyor. Sonuçlar aşağıda gösterilmektedir:

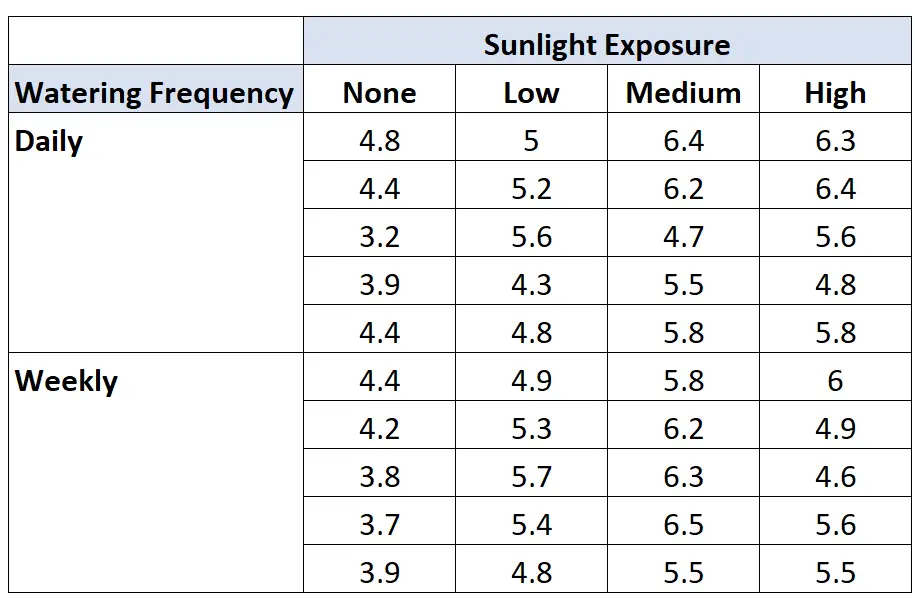
Profesör iki yönlü bir ANOVA gerçekleştirir ve aşağıdaki sonuçları elde eder:

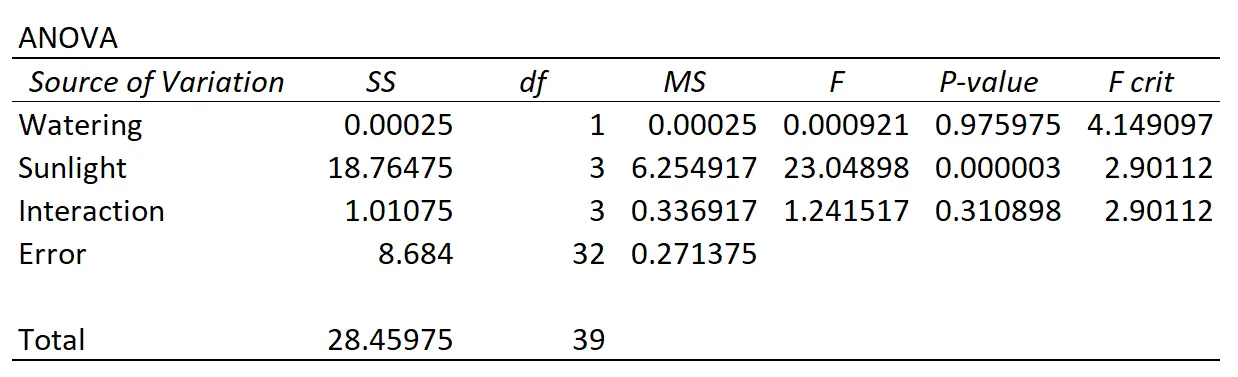
Sonuçları nasıl yorumlayacağınız aşağıda açıklanmıştır:

• Sulama sıklığı ile güneşe maruz kalma arasındaki etkileşimin p değeri 0,310898 idi. Bu durum 0,05 alfa düzeyinde istatistiksel olarak anlamlı değildir.
• Sulama sıklığına ilişkin p değeri 0,975975’tir . Bu durum 0,05 alfa düzeyinde istatistiksel olarak anlamlı değildir.
• Güneşe maruz kalmanın p değeri 0,000003 idi. Bu, 0,05 alfa seviyesinde istatistiksel olarak anlamlıdır.

Bu sonuçlar, bitki boyu üzerinde istatistiksel olarak anlamlı etkiye sahip tek faktörün güneşe maruz kalma olduğunu göstermektedir.

Etkileşim etkisi olmadığından güneşe maruz kalmanın etkisi, sulama sıklığının her seviyesinde tutarlıdır. Basitçe söylemek gerekirse, bir bitkinin günlük veya haftalık olarak sulanmasının, güneşe maruz kalmanın bitkiyi nasıl etkilediği üzerinde hiçbir etkisi yoktur.

Pratik: Hangi ANOVA’yı kullanmalısınız?

Tek yönlü veya iki yönlü ANOVA’yı ne zaman kullanmanız gerektiğini daha iyi anlamak için aşağıdaki uygulama problemlerini kullanın.

Sorun #1: Tarım

Bir çiftçi, üç farklı gübrenin farklı verim sağlayıp sağlamadığını bilmek istiyor. Bunu test etmek için her tür gübreyi 10 farklı tarlaya serpiyor ve büyüme mevsimi sonundaki toplam verimi ölçüyor.

Farklı gübrelerin farklı ürün verimine yol açıp açmadığını belirlemek için ne tür ANOVA kullanmalıdır?

Cevap: Tek yönlü ANOVA kullanmalıdır çünkü yalnızca tek bir faktöre bakmaktadır: gübre. Tek yönlü bir ANOVA, ona üç farklı gübre türü arasında mahsul verimi açısından istatistiksel olarak anlamlı bir fark olup olmadığını söyleyebilir.

Sorun #2: Biyoloji

Bir biyolog, farklı toprak seviyelerinin (düşük, orta, yüksek) ve sulama sıklıklarının (haftalık, aylık) belirli bir bitkinin büyümesini nasıl etkilediğini bilmek ister.

Farklı güneşe maruz kalma ve sulama sıklığı kombinasyonlarının farklı bitki büyümesi düzeylerine yol açıp açmadığını belirlemek için ne tür ANOVA kullanılmalıdır?

Cevap: İki yönlü bir ANOVA kullanmalıdır çünkü iki faktöre bakmaktadır: güneş ışığına maruz kalma ve sulama sıklığı. İki yönlü bir ANOVA, her faktörün farklı seviyelerinin bitki büyümesini farklı şekilde etkileyip etkilemediğini ve güneş ışığı ile sulama sıklığı arasında bitki büyümesi üzerinde bir etkileşim etkisinin olup olmadığını söyleyebilir.

Sorun 3: İlaçlar

Bir tıbbi araştırmacı, dört farklı ilacın hastalarda kan basıncında farklı ortalama düşüşlere neden olup olmadığını bilmek istiyor. Her ilacı bir ay boyunca kullanacak 20 hastayı rastgele seçiyor ve ardından her hastadaki kan basıncındaki düşüşü ölçüyor.

Dört farklı ilacın kan basıncını düşürmede farklı etkileri olup olmadığını belirlemek için ne tür ANOVA kullanılmalıdır?

Cevap: Tek yönlü ANOVA kullanmalıdır çünkü yalnızca tek bir faktöre bakmaktadır: ilacın türüne. Tek yönlü bir ANOVA, dört ilaç türü arasında ortalama kan basıncı düşüşünde istatistiksel olarak anlamlı bir fark olup olmadığını söyleyebilir.

Ek kaynaklar

Tek yönlü ANOVA’yı daha iyi anlamak için aşağıdaki eğitimleri kullanın:

• Tek Yönlü ANOVA’ya Giriş
• Excel’de Tek Yönlü ANOVA Nasıl Gerçekleştirilir
• R’de tek yönlü ANOVA nasıl gerçekleştirilir

İki yönlü ANOVA’yı daha iyi anlamak için bu eğitimleri kullanın:

• İki Yönlü ANOVA’ya Giriş
• Excel’de İki Yönlü ANOVA Nasıl Gerçekleştirilir
• R’de iki yönlü ANOVA nasıl gerçekleştirilir