Spss'de tekrarlanan ölçümler anova nasıl gerçekleştirilir

Tekrarlanan ölçümler ANOVA, her grupta aynı deneklerin yer aldığı üç veya daha fazla grubun ortalamaları arasında istatistiksel olarak anlamlı bir fark olup olmadığını belirlemek için kullanılır.

Bu eğitimde SPSS’de tek yönlü tekrarlı ölçüm ANOVA’sının nasıl gerçekleştirileceği açıklanmaktadır.

Örnek: SPSS’de Tekrarlanan Ölçümler ANOVA

Araştırmacılar dört farklı ilacın farklı reaksiyon sürelerine neden olup olmadığını bilmek istiyorlar. Bunu test etmek için beş hastanın dört farklı ilaca reaksiyon sürelerini ölçtüler. Her hasta dört ilacın her birinde ölçüldüğü için, ortalama reaksiyon süresinin ilaçlar arasında farklılık gösterip göstermediğini belirlemek için tekrarlanan ölçümler ANOVA’sını kullanacağız.

SPSS’de tekrarlanan ölçümler ANOVA’yı gerçekleştirmek için aşağıdaki adımları tamamlayın.

Adım 1: Verileri girin.

Beş hastanın dört ilaca yanıt verme süresini (saniye cinsinden) gösteren aşağıdaki verileri girin:

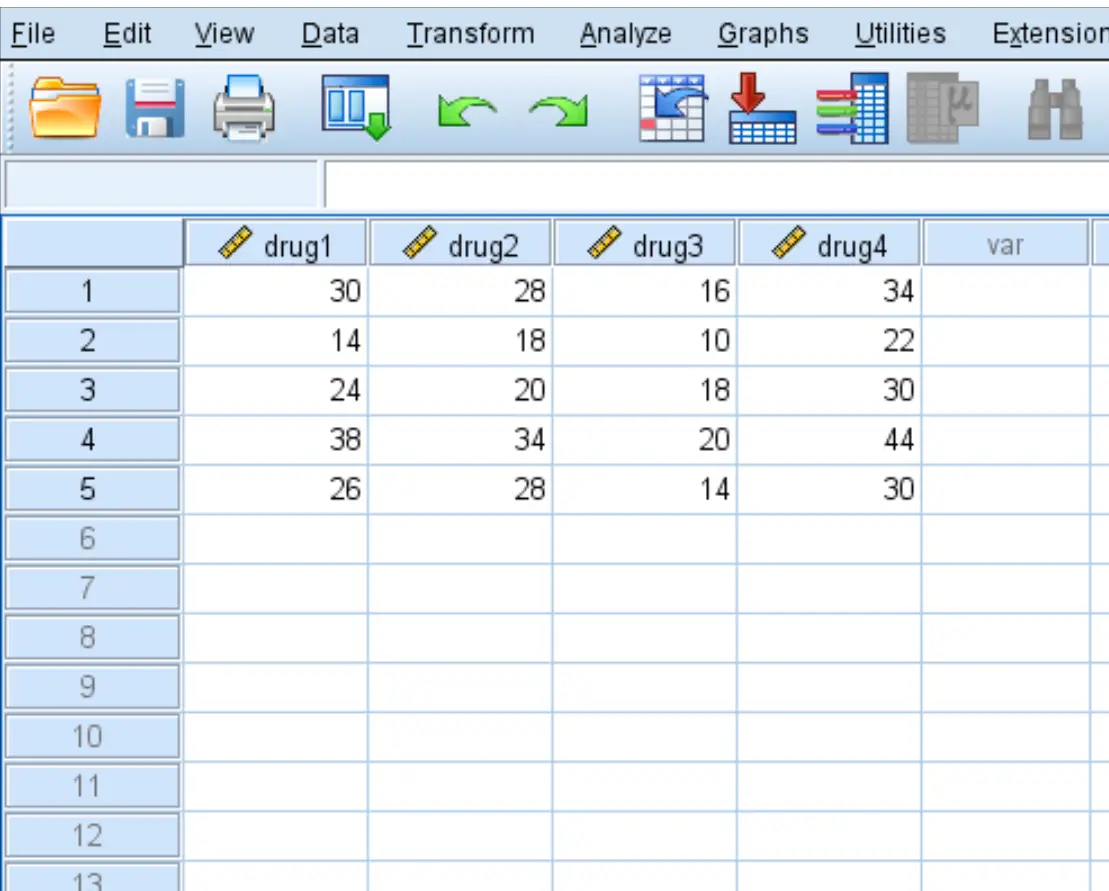
Adım 2: Tekrarlanan ölçüm ANOVA’sını gerçekleştirin.

Analiz sekmesine, ardından Genel Doğrusal Model’e ve ardından Tekrarlanan Ölçümler’e tıklayın:

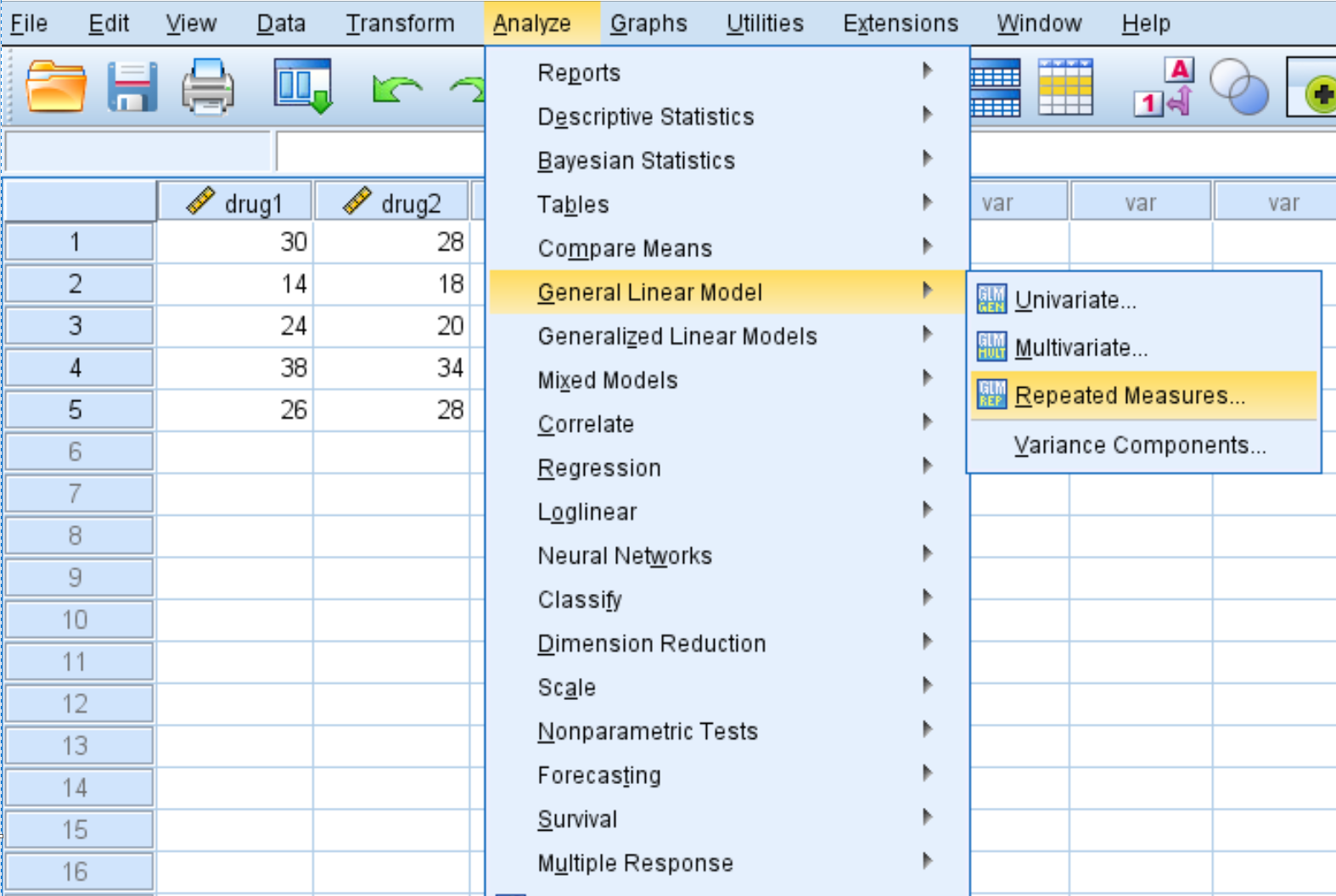
Açılan yeni pencerede, konu içi faktör adı için ilacı girin. Seviye sayısı için 4 yazın (her çalışma katılımcısı 4 farklı ilacı test ettiği için), ardından Ekle’ye tıklayın. Ölçü Adı için ResponseTime yazın ve ardından Ekle’ye tıklayın. Son olarak Ayarla’yı tıklayın.

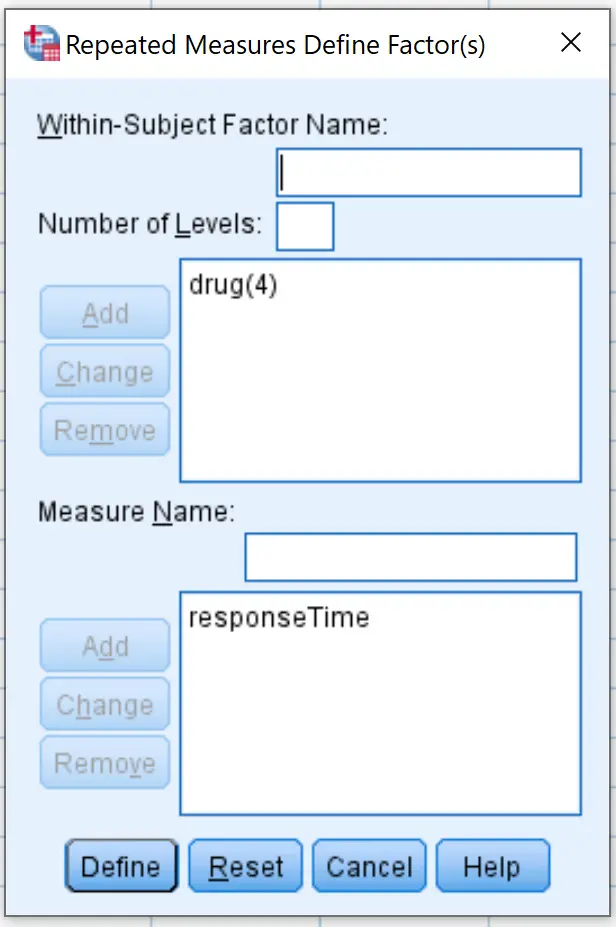
Görünen yeni pencerede, dört ilaç değişkeninin her birini Denek İçi Değişkenler etiketli alana sürükleyin:

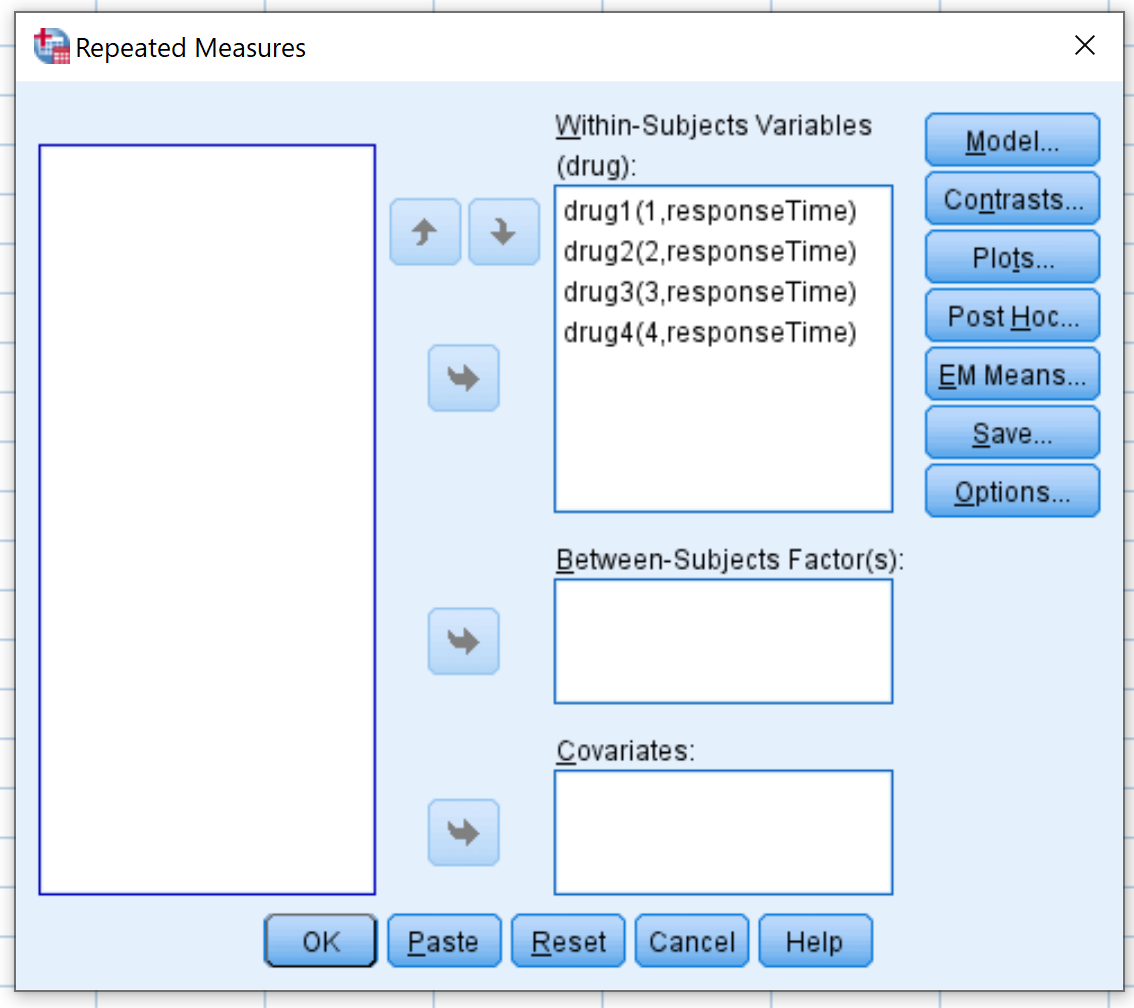
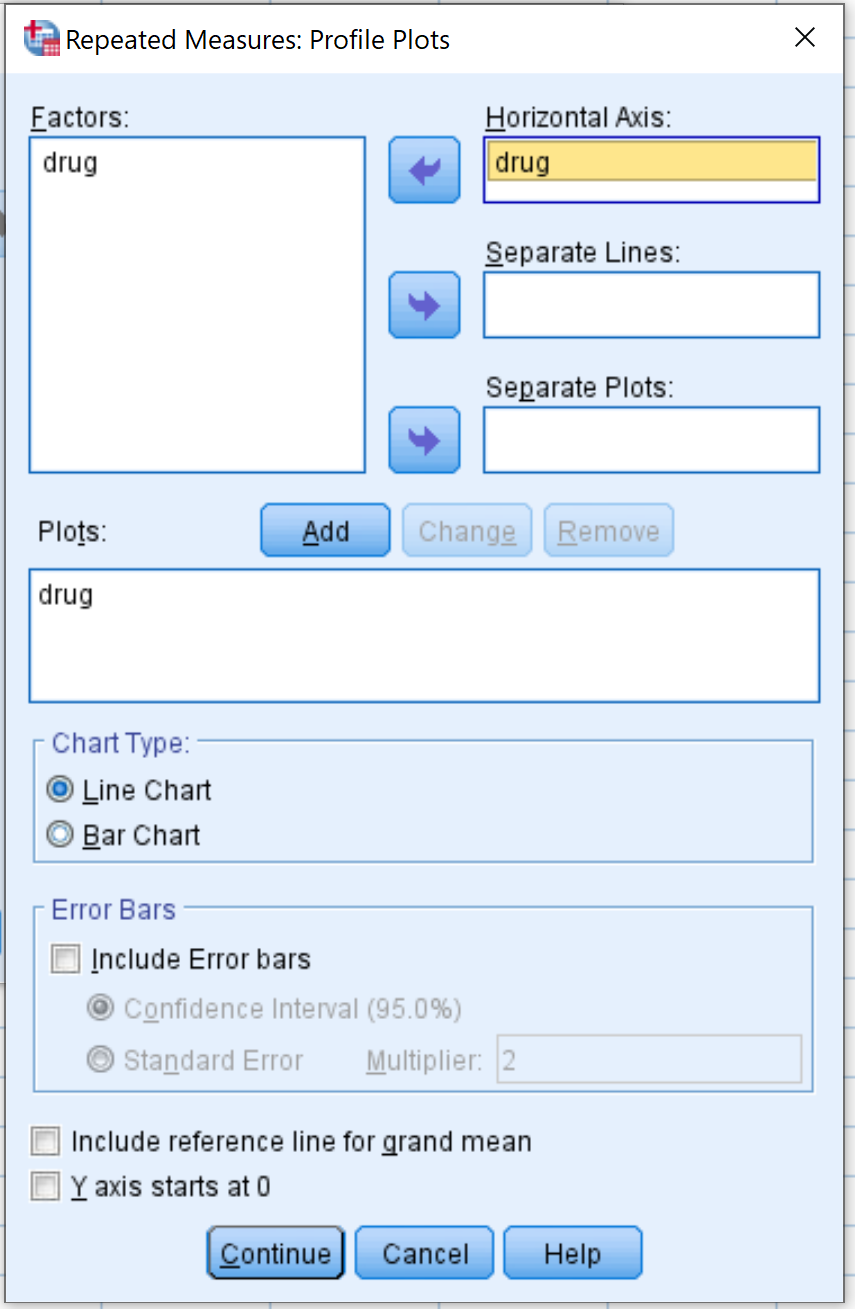
Daha sonra Grafikler’e tıklayın. Değişken ilacı Yatay Eksen etiketli alana sürükleyin. Daha sonra Ekle’yi tıklayın. Daha sonra Devam’ı tıklayın.

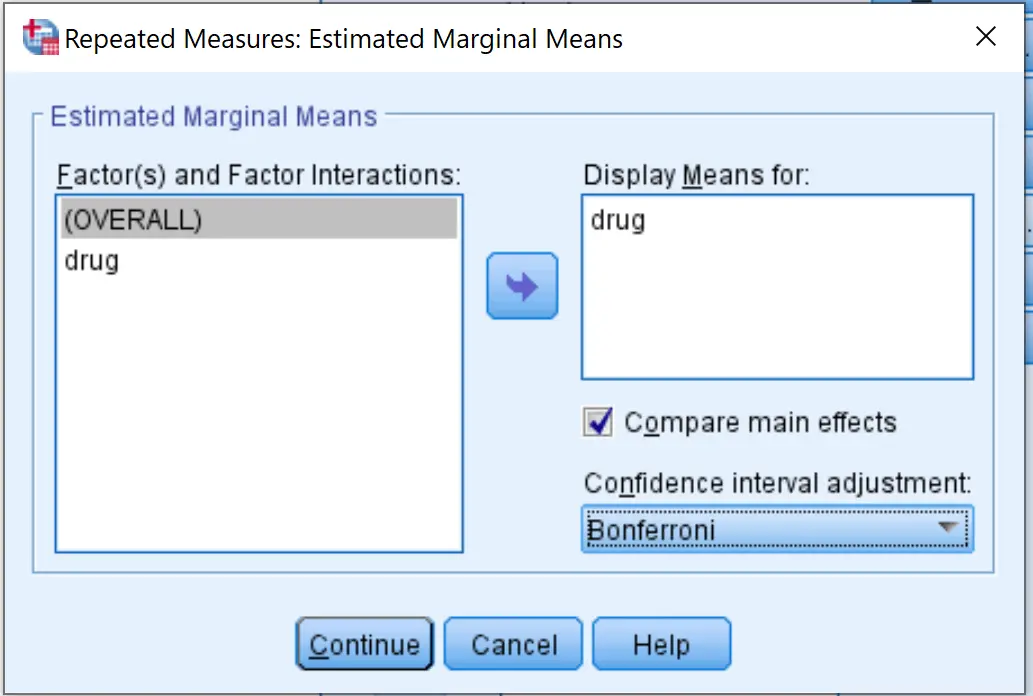
Daha sonra EM Anlamına tıklayın. İlaç değişkenini Şunun Anlamını Göster etiketli kutuya sürükleyin. Ardından Ana efektleri karşılaştır’ın yanındaki kutuyu işaretleyin ve açılır menüden Bonferroni’yi seçin. Daha sonra Devam’ı tıklayın.

Son olarak Tamam’ı tıklayın.

Adım 2: Sonuçları yorumlayın.

Tamam’a tıkladığınızda, tekrarlanan ölçümlerin sonuçları ANOVA görünecektir. Sonucun nasıl yorumlanacağı aşağıda açıklanmıştır:

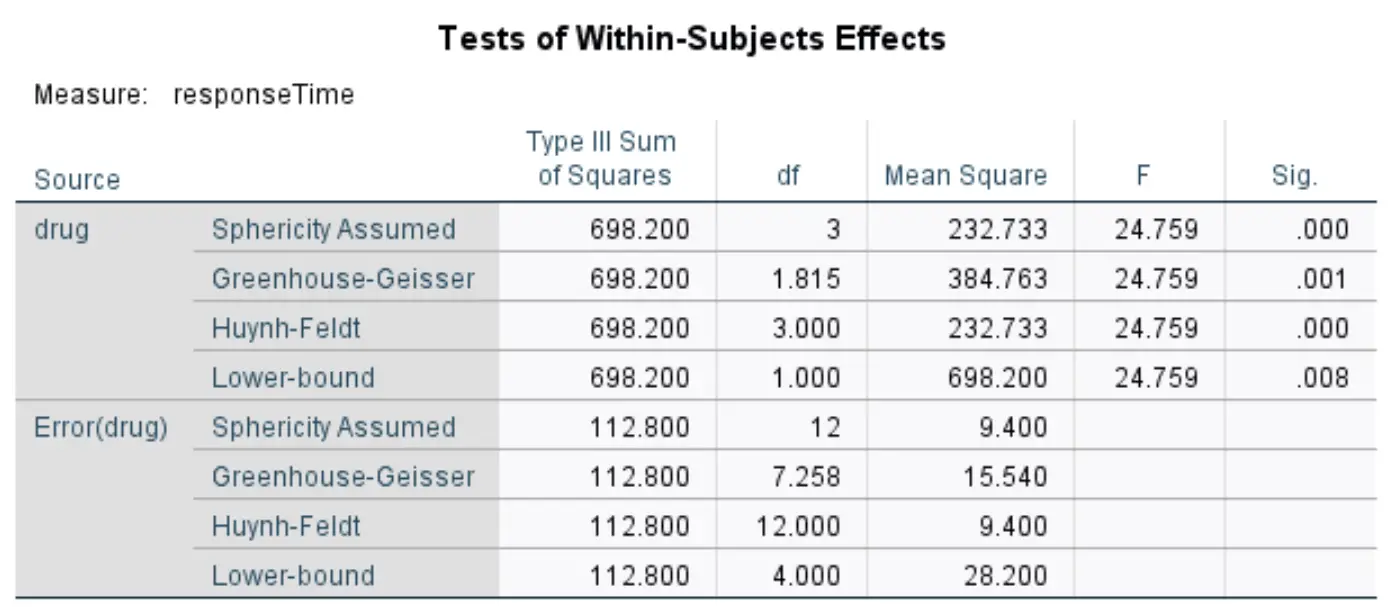
Denek içi etki testleri

Bu tablo genel F istatistiğini ve tekrarlanan ölçümlerin ANOVA’sından karşılık gelen p değerini görüntüler. Genelde Greenhouse-Geisser etiketli satırdaki değerleri kullanıyoruz.

Bu doğruya göre F istatistiği 24,759 ve buna karşılık gelen p değeri 0,001’dir . Bu p değeri 0,05’ten küçük olduğundan sıfır hipotezini reddedebilir ve dört ilaç arasındaki ortalama yanıt sürelerinde istatistiksel olarak anlamlı bir fark olduğu sonucuna varabiliriz.

İkili karşılaştırma

Sıfır hipotezini reddettiğimize göre bu, en az iki grup ortalamasının farklı olduğu anlamına gelir. Hangi ortalama gruplarının farklı olduğunu belirlemek için her ilaç arasındaki ikili karşılaştırmaları gösteren bu tabloyu kullanabiliriz.

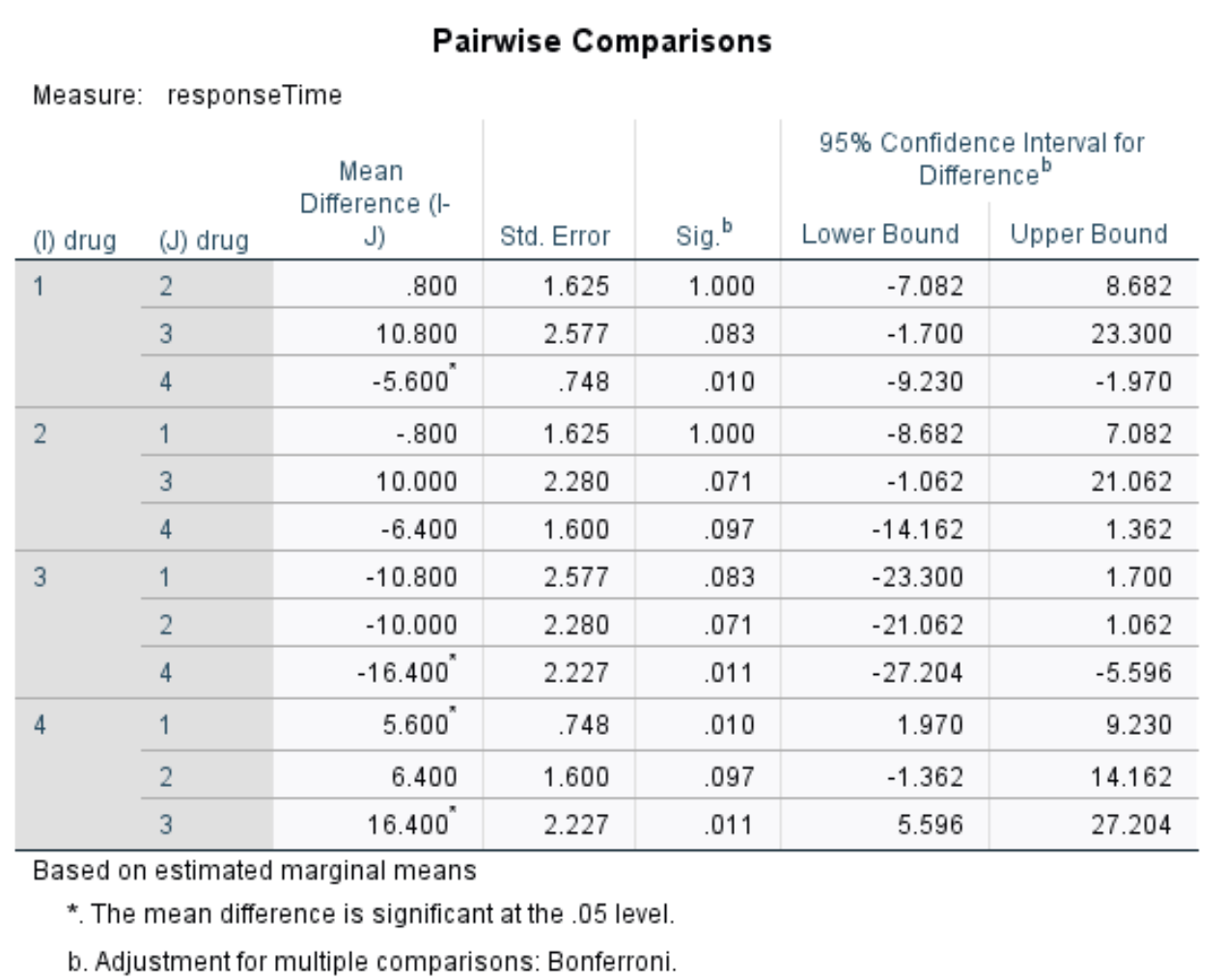
Tabloda aşağıdaki karşılaştırmalar için p değerlerini görebiliriz:

• ilaç 1’e karşı ilaç 2 | p-değeri = 1.000
• ilaç 1’e karşı ilaç 3 | p-değeri = 0,083
• ilaç 1’e karşı ilaç 4 | p-değeri = 0,010
• ilaç 2’ye karşı ilaç 3 | p-değeri = 0,071
• ilaç 2’ye karşı ilaç 4 | p-değeri = 0,097
• ilaç 3’e karşı ilaç 4 | p-değeri = 0,011

0,05’ten küçük p değerleri yalnızca ilaç 1’e karşı ilaç 4 ve ilaç 3’e karşı ilaç 4 içindir. Diğer tüm karşılaştırmalarda p değerleri 0,05’ten büyüktür.

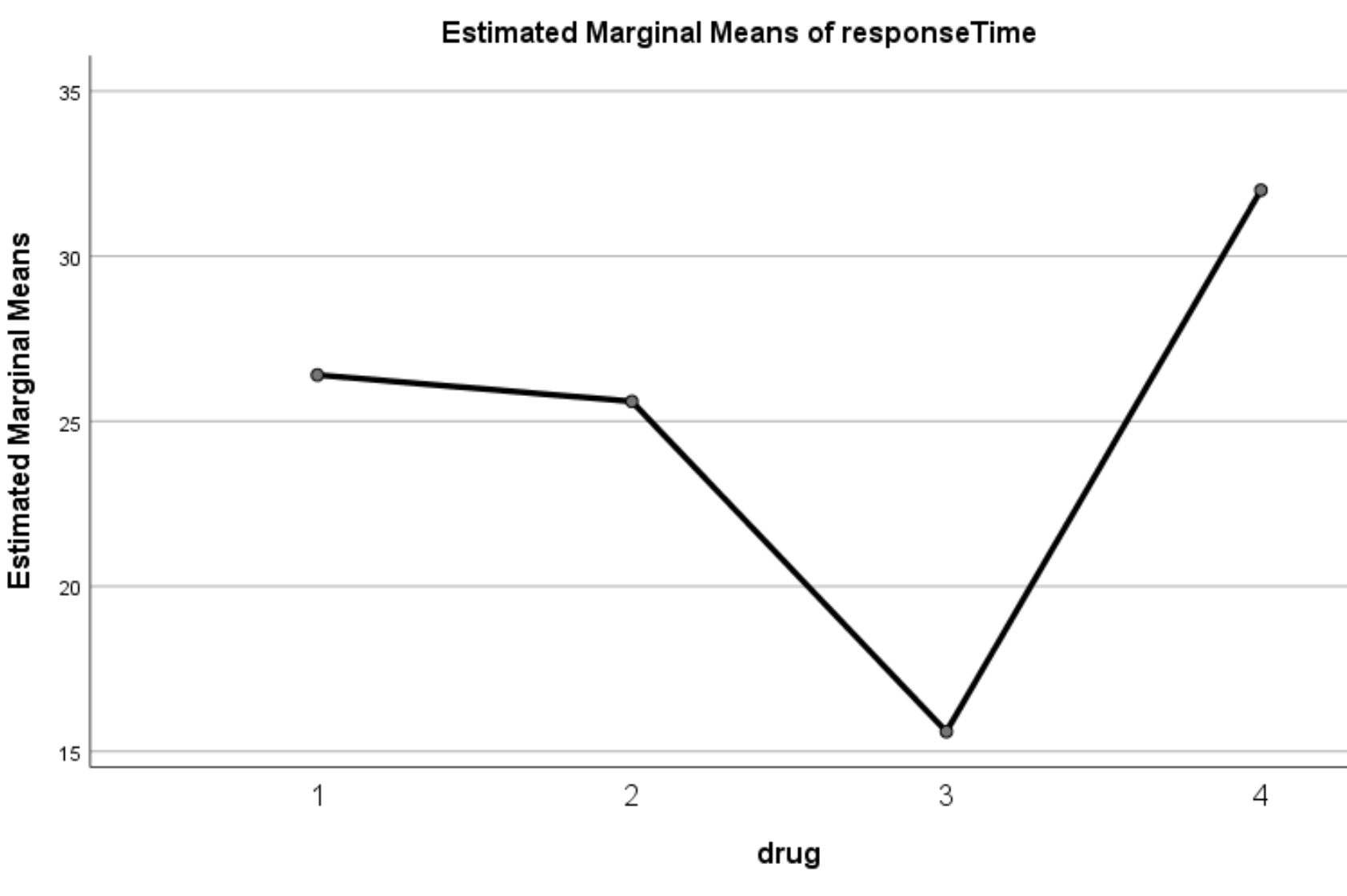
Tahmini marjinal ortalamaların grafiği

Bu grafik, her ilaç için tahmini ortalama yanıt sürelerini gösterir. Grafikten, yanıt sürelerinin dört farklı ilaç arasında önemli ölçüde farklılık gösterdiğini açıkça görebiliriz:

Adım 3: Sonuçları rapor edin.

Son olarak tekrarlanan ölçümlerin sonuçlarını ANOVA olarak raporlayabiliriz. İşte bunun nasıl yapılacağına dair bir örnek:

Hastaların ortalama reaksiyon süresinin dört farklı ilaç arasında farklılık gösterip göstermediğini belirlemek için tek yönlü tekrarlanan ölçümlü ANOVA yapıldı.

Tek yönlü tekrarlanan ölçümler ANOVA, kullanılan ilaç türünün yanıt süresinde istatistiksel olarak anlamlı farklılıklara yol açtığını ortaya çıkardı (F = 24,75887, p = 0,001).

Çoklu karşılaştırmalar için Bonferroni testi, ilaç 1 ve ilaç 4’ün yanı sıra ilaç 3 ve ilaç 4’ü alan hastalar arasında yanıt sürelerinde istatistiksel olarak anlamlı bir fark olduğunu ortaya çıkardı.