Ti-84 hesap makinesinde i̇kinci dereceden regresyon nasıl gerçekleştirilir

İki değişkenin doğrusal bir ilişkisi olduğunda, ilişkilerini ölçmek için sıklıkla basit doğrusal regresyon kullanabiliriz .

Bununla birlikte, iki değişken ikinci dereceden bir ilişkiye sahip olduğunda, ilişkilerini ölçmek için ikinci dereceden regresyonu kullanabiliriz.

Bu eğitimde, bir TI-84 hesap makinesinde ikinci dereceden regresyonun nasıl gerçekleştirileceği açıklanmaktadır.

Örnek: TI-84 hesap makinesinde ikinci dereceden regresyon

Çalışılan saat sayısı ile mutluluk arasındaki ilişkiyi anlamak istediğimizi varsayalım. 11 farklı kişi için haftada çalışılan saat sayısı ve rapor edilen mutluluk düzeyi (0’dan 100’e kadar bir ölçekte) hakkında aşağıdaki verilere sahibiz:

TI-84 hesap makinesinde ikinci dereceden regresyon gerçekleştirmek için aşağıdaki adımları izleyin.

Adım 1: Verileri görselleştirin.

İkinci dereceden regresyonu kullanmadan önce, açıklayıcı değişken (saat) ile yanıt değişkeni (mutluluk) arasındaki ilişkinin gerçekten ikinci dereceden olduğundan emin olmalıyız.

Öncelikle açıklayıcı değişken ve yanıt değişkeni için veri değerlerini gireceğiz. Stat’a ve ardından EDIT’e basın. Açıklayıcı değişken (çalışılan saat) için aşağıdaki değerleri L1 sütununa ve yanıt değişkeni (mutluluk) için değerleri L2 sütununa girin:

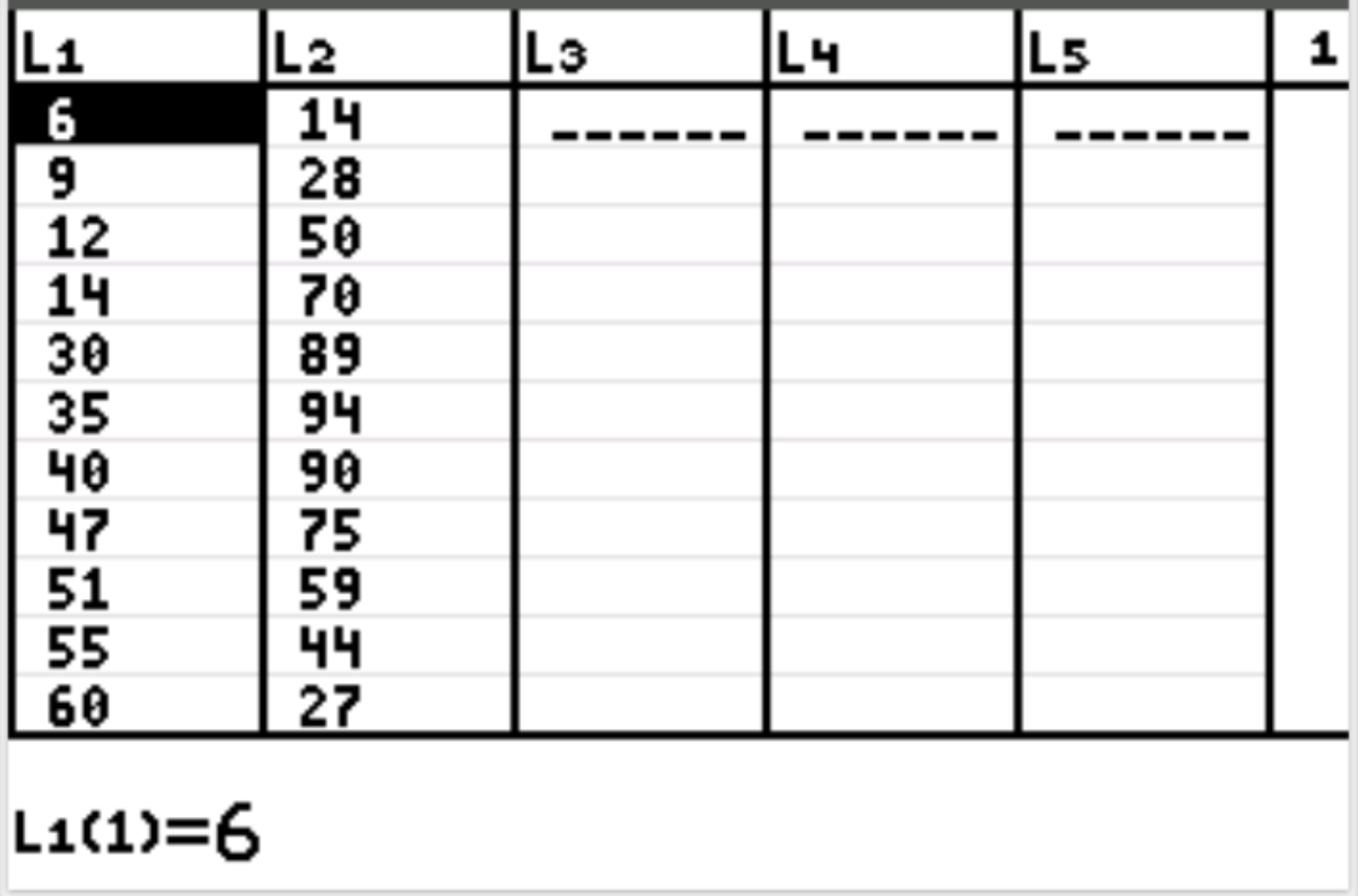
Daha sonra istatistik grafiği menüsüne erişmek için 2’ye ve ardından y= tuşuna basın. Grafik1’i vurgulayın ve Enter’a basın. Çizimin etkinleştirildiğinden ve Xlist ve Ylist için sırasıyla L1 ve L2’nin seçildiğinden emin olun:

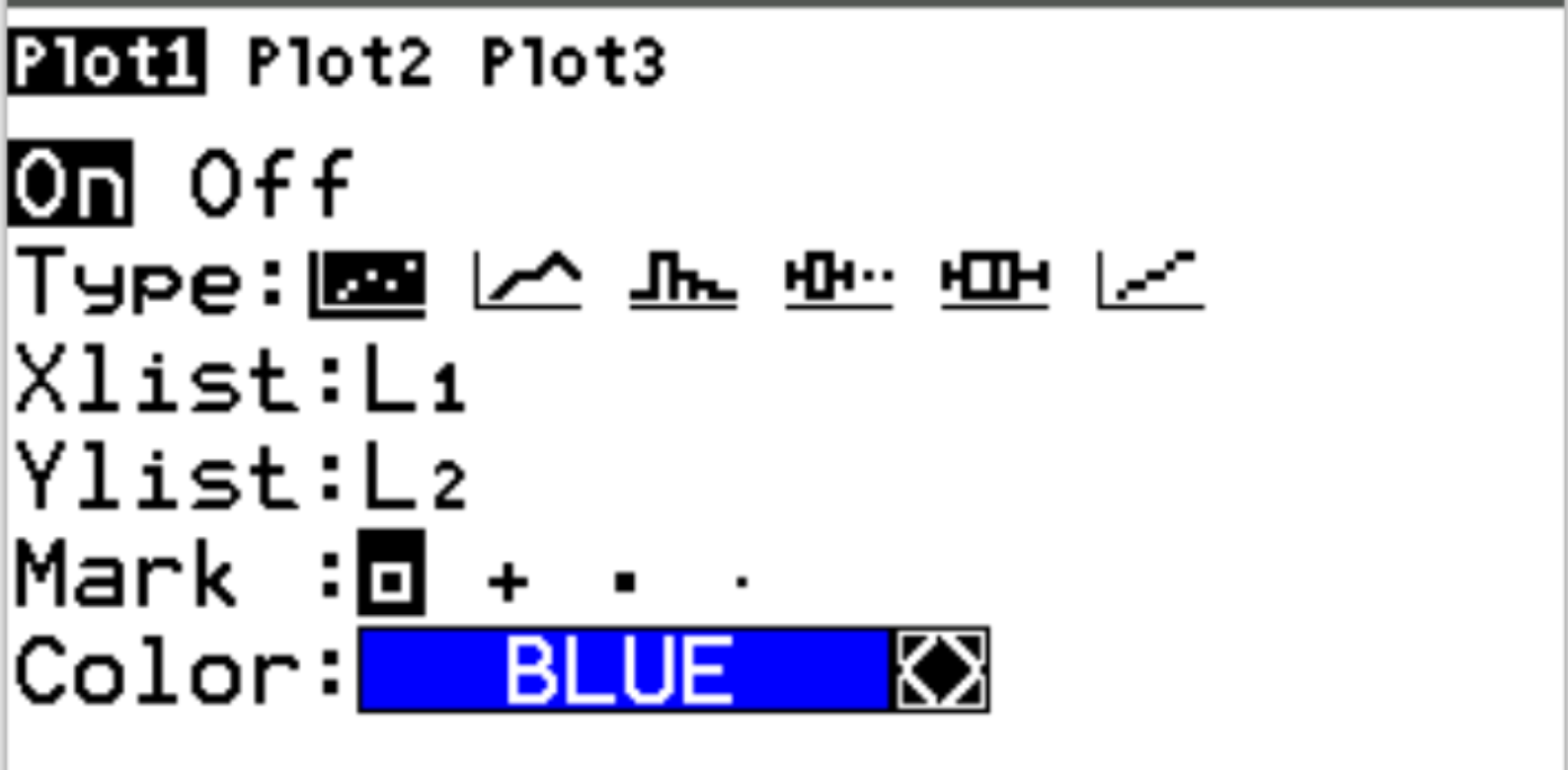
Ardından yakınlaştır’a ve ardından 9:ZoomStat’a basın. Bu otomatik olarak aşağıdaki nokta bulutunu üretecektir:

Mutluluğun, çalışılan saat sayısı sıfırdan belirli bir noktaya kadar arttıkça artma eğiliminde olduğunu, ancak daha sonra çalışılan saat sayısı arttıkça azalmaya başladığını görebiliriz.

Dağılım grafiğindeki bu ters “U” şekli, çalışılan saat ile mutluluk arasında ikinci dereceden bir ilişki olduğunu gösterir; bu, bu ilişkiyi ölçmek için ikinci dereceden regresyon kullanmamız gerektiği anlamına gelir.

Adım 2: İkinci dereceden regresyon gerçekleştirin.

Daha sonra ikinci dereceden regresyon gerçekleştireceğiz. Stat’a basın ve ardından CALC’ye gidin. Daha sonra 5:QuadReg’e gidin ve Enter tuşuna basın.

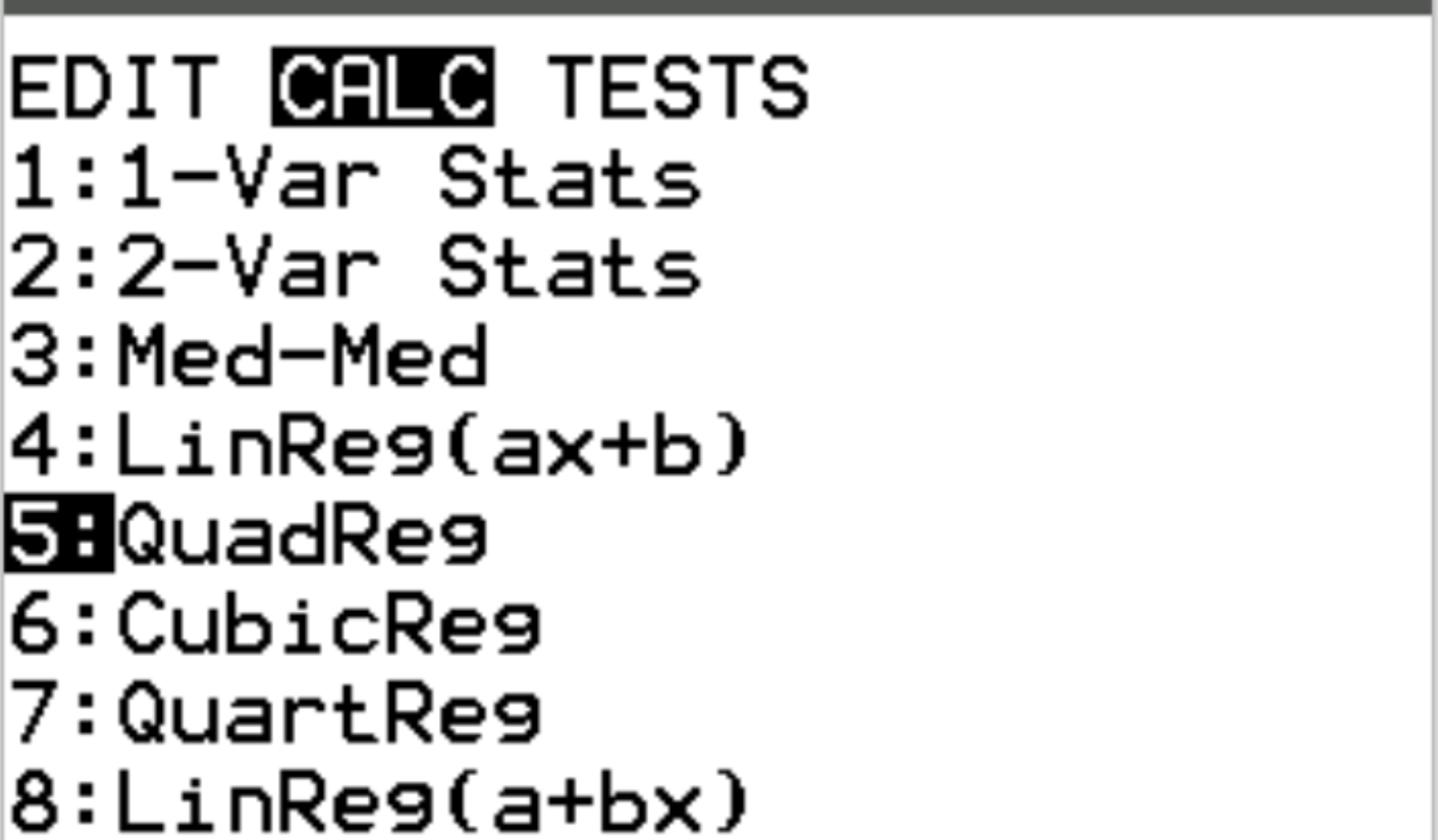
Xlist ve Ylist için L1 ve L2’nin seçildiğinden emin olun çünkü bunlar verilerimizi girmek için kullandığımız sütunlardır. FreqList’i boş bırakın. Hesapla seçeneğine ilerleyin ve Enter tuşuna basın.

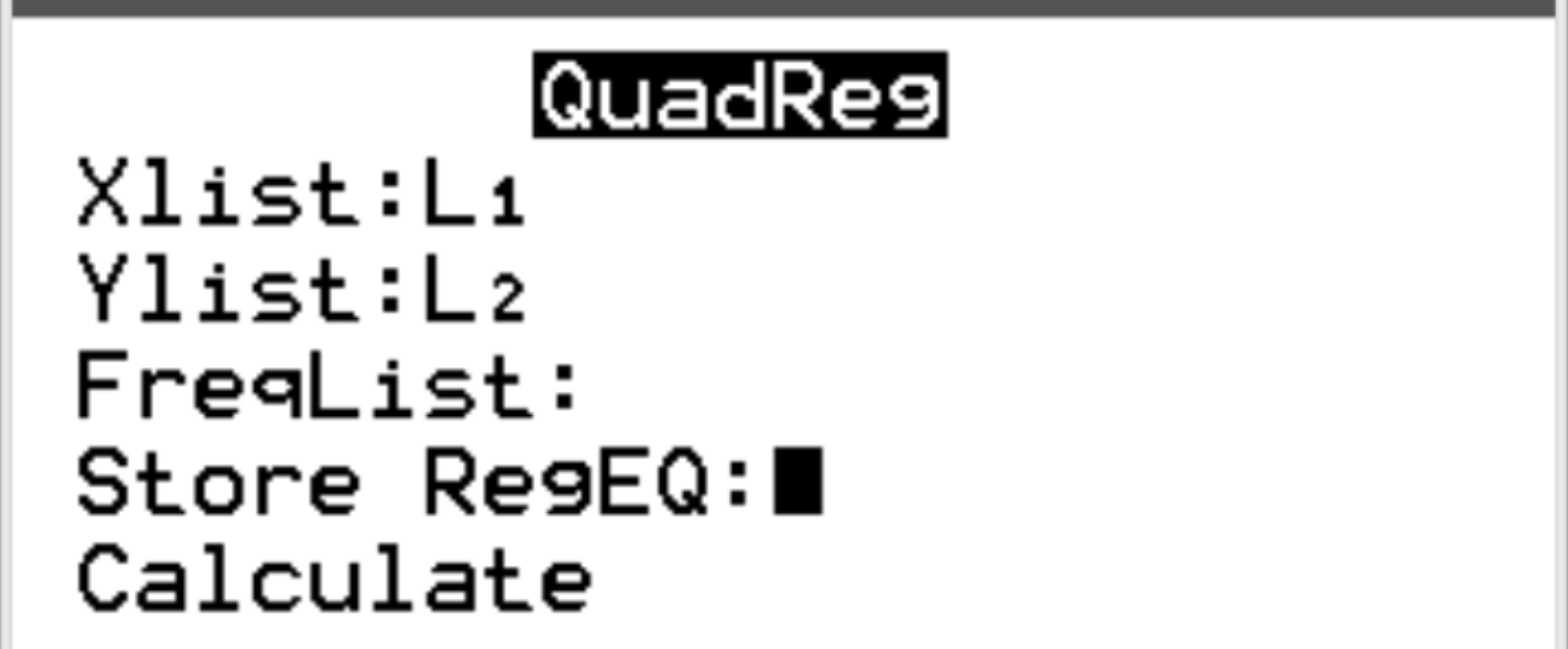
Aşağıdaki çıktı otomatik olarak görünecektir:

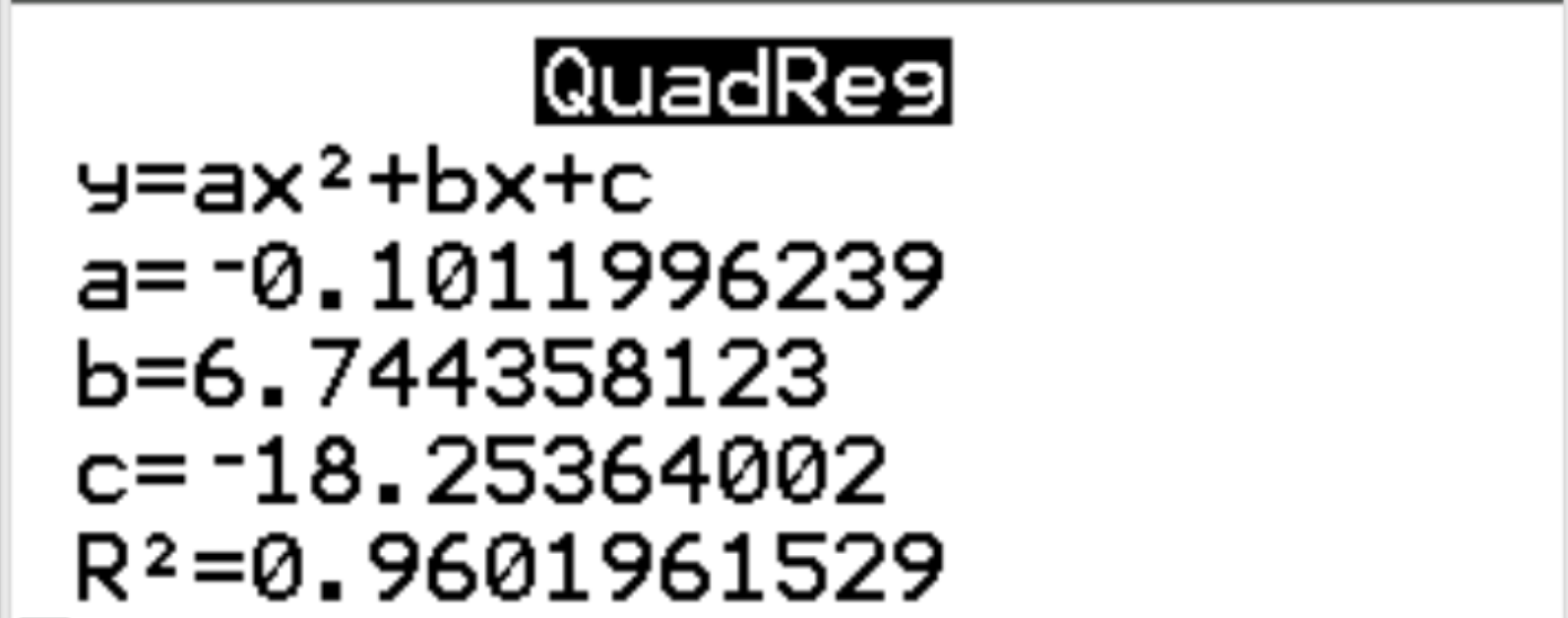
Adım 3: Sonucu yorumlayın.

Sonuçlardan tahmin edilen regresyon denkleminin şu şekilde olduğunu görebiliriz:

mutluluk = -0,1012 (saat) ² + 6,7444 (saat) – 18,2536

Bu denklemi, bir bireyin haftada kaç saat çalıştığı göz önüne alındığında tahmin edilen mutluluğunu bulmak için kullanabiliriz.

Örneğin haftada 60 saat çalışan bir kişinin mutluluk düzeyi 22,09 olacaktır:

mutluluk = -0,1012(60) ² + 6,7444(60) – 18,2536 = 22,09

Haftada 30 saat çalışan bir kişinin ise mutluluk düzeyi 92,99 olmalıdır:

mutluluk = -0,1012(30) ² + 6,7444(30) – 18,2536 = 92,99

Regresyon modeli için r karenin r ² = 0,9602 olduğunu da görebiliriz. Bu, açıklayıcı değişkenler tarafından açıklanabilen yanıt değişkenindeki varyansın oranıdır. Bu örnekte mutluluktaki değişimin %96,02’si saat ve saatlerle açıklanabilmektedir ² .