Yazıyor

İle Dr.benjamin anderson Ağustos 5, 2023 İstatistik 0 Yorum

Bu makale istatistikte bir dağılımı karakterize etmenin ne anlama geldiğini açıklamaktadır. Böylece tiplendirmenin tanımını, bir değişkenin tiplendirme örneğini bulacak ve ayrıca adım adım çözülen bir alıştırma ile pratik yapabileceksiniz.

Yazmak nedir?

İstatistikte normalizasyon , bir dağılıma, ortalaması ve standart sapması sırasıyla sıfır ve bire eşit olacak şekilde doğrusal bir dönüşümün uygulandığı bir süreçtir.

Daha doğrusu, tipleme, ortalamanın rastgele değişkenden çıkarılmasını ve ardından standart sapmaya bölünmesini içerir.

Yazmaya normalizasyon veya standardizasyon da denilebilir.

Giriş formülü

Bir değişkeni sınıflandırmak için ortalamasını çıkarmanız ve ardından standart sapmasına bölmeniz gerekir. Bu nedenle bir değişken girme formülü aşağıdaki gibidir:

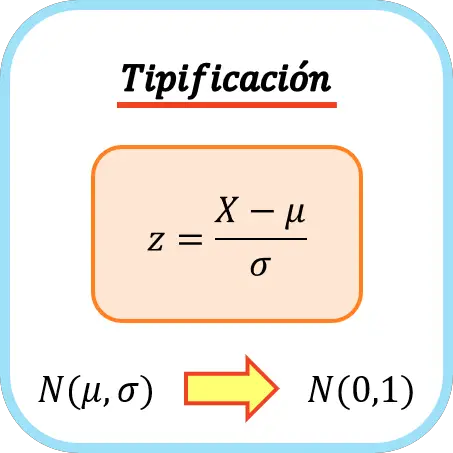
Altın

$\mu$

değişkenin ortalamasıdır

$X$

$\sigma$

standart sapması (veya standart sapması).

Bu nedenle değişkene doğrusal bir dönüşüm uygulandığından giriş aslında bir değişken değişikliğidir.

Örnek giriş

Aşağıda tiplendirmenin tanımı ve formülü dikkate alındığında kavramın tam olarak anlaşılabilmesi için somut bir örnek verilmiştir.

Sürekli bir rastgele değişken, ortalaması 45 ve standart sapması 10 olan normal bir dağılım izlemektedir; 60’tan küçük veya buna eşit bir değer elde etme olasılığı nedir?

$N(45,10)$

Normal dağılım olasılığını bulmak için karakteristik tablosunu kullanmamız gerekir, ancak bunu yapmak için önce yazma işlemini gerçekleştirmemiz gerekir. Yani ortalamayı çıkarıp standart sapmaya bölerek olasılık değerine bölüyoruz:

$\displaystyle P(X\leq 60)=P\left(Z\leq\frac{60-45}{10}\right)=P(Z\leq 1,5)$

Standardize ettikten sonra, 1,5 değerinin hangi olasılığa karşılık geldiğini görmek için normal dağılım olasılık tablosuna geçiyoruz:

Normal dağılım tiplendirme tablosunda görüldüğü gibi bir önceki adımda hesaplanan değer aşağıdaki olasılığa karşılık gelmektedir:

$\displaystyle P(Z\leq 1,5)=0,9332$

Dolayısıyla 60’a eşit veya daha küçük bir değer elde etme olasılığı %93,32’dir.

Yazma Alıştırması Çözüldü

Ortalaması ve standart sapması sırasıyla 120 ve 50 olan bir normal dağılımın aşağıdaki olasılıklarını hesaplayın.

$N(120,50)$

208’den küçük veya ona eşit bir değer elde etme olasılığı.
137’den büyük bir değer elde etme olasılığı.

Çözümü görün

Problemin her iki bölümünde de olasılıkları hesaplamak için normal dağılımı yazmamız gerekiyor.

208’den küçük veya ona eşdeğer bir değerin olasılık tipini hesaplayarak başlıyoruz:

$\displaystyle P(X\leq 208)=P\left(Z\leq\frac{208-120}{50}\right)=P(Z\leq 1,76)$

Şimdi yukarıdaki tabloya 1,76 değerinin hangi olasılığa karşılık geldiğine bakalım:

$\displaystyle P(Z\leq 1,76)=0,9608$

İkinci olarak 137’den büyük bir değer elde etme olasılığını hesaplayacağız. Aynı şekilde değişkeni yazarak başlıyoruz:

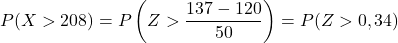$\displaystyle P(X> 208)=P\left(Z>\frac{137-120}{50}\right)=P(Z>0,34)” title=”Rendered by QuickLaTeX.com” height=”43″ width=”398″ style=”vertical-align: -17px;”> <p class=$ Bununla birlikte, ekteki tablo yalnızca en düşük kümülatif olasılıklara sahiptir, bu nedenle tabloyu kullanmak için öncelikle olasılığı dönüştürmemiz gerekir:

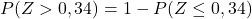$\displaystyle P(Z>0,34)=1-P(Z\leq 0,34)” title=”Rendered by QuickLaTeX.com” height=”19″ width=”252″ style=”vertical-align: -5px;”> <p class=$ Ve son olarak, ekteki tablodan Z’nin hesaplanan değerine karşılık gelen olasılığı not edeceğiz:

$\displaystyle P(Z>0,34)=1-P(Z\leq 0,34)=1-0,6331=0,3669″ title=”Rendered by QuickLaTeX.com” height=”19″ width=”435″ style=”vertical-align: -5px;”> <div class=$

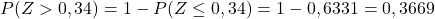
Yazmanın amacı nedir?

Tiplendirmenin anlamını anlamayı tamamlamak için, bunun ne için kullanıldığını ve bir değişkenin ne zaman yazılması gerektiğini göreceğiz.

Temel olarak standardizasyon, dağılımların değerlerini farklı ortalama ve varyanslarla karşılaştırmak için kullanılır. Benzer şekilde, bir olasılığı hesaplamak için standardizasyon da kullanılır.

Farklı özelliklere sahip dağılımların iki değerini standartlaştırarak, dağılımın tamamına göre hangi değerin daha büyük veya daha küçük olduğunu görebiliriz. Veya başka bir deyişle tiplendirme işlemini uygulayarak hangi değerin dağılım ortalamasına en yakın veya en uzak olduğunu görebiliriz.

Ek olarak, yukarıda açıklandığı gibi, olasılık tabloları genel olarak tiplendirilmiş bir dağılıma dayandığından tiplendirme olasılıkların hesaplanmasına da olanak tanır.

yazar hakkında

Dr.benjamin anderson

Merhaba, ben Benjamin, emekli bir istatistik profesörü ve Statorials öğretmenine dönüştüm. İstatistik alanındaki kapsamlı deneyimim ve uzmanlığımla, öğrencilerimi Statorials aracılığıyla güçlendirmek için bilgilerimi paylaşmaya can atıyorum. Daha fazlasını bil