Toplama kuralı (veya ekleme kuralı)

İle Dr.benjamin anderson Ağustos 1, 2023 Olasılık 0 Yorum

Bu makalede, toplama kuralı olarak da bilinen toplama kuralının ne olduğu, olasılık ve istatistikte ne için kullanıldığı anlatılmaktadır. Ayrıca toplama kuralı formülünün ne olduğunu ve bu formülün nasıl kullanılacağını gösteren çözülmüş alıştırmaları görebileceksiniz.

Toplama kuralı (veya toplama kuralı) nedir?

Toplama kuralı (veya toplama kuralı ), iki olayın olasılıklarının toplamının, her bir olayın ayrı ayrı meydana gelme olasılığı eksi her iki olayın aynı anda meydana gelme olasılığı toplamına eşit olduğunu belirtir.

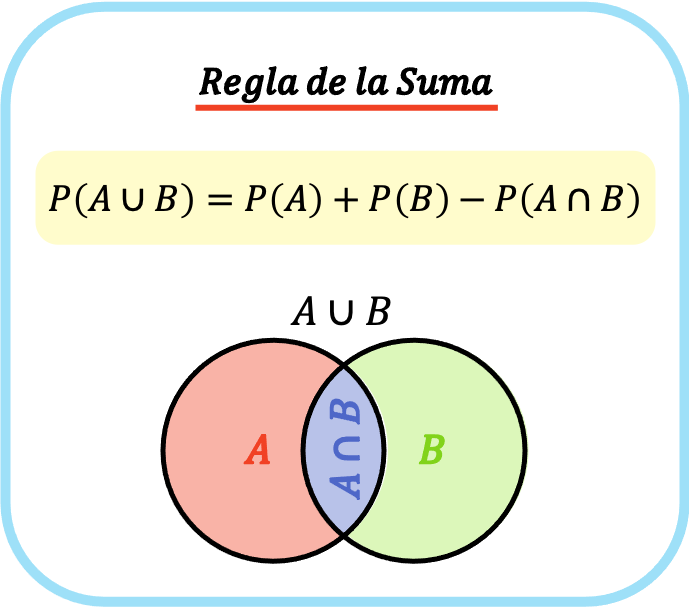
Bu nedenle toplama kuralının formülü P(A⋃B)=P(A)+P(B)−P(A⋂B) şeklindedir.

Bu nedenle, iki olasılığı toplamak için her olasılığı basitçe ekleyemeyiz, çünkü iki olayın ortak olasılığını temsil eden terimi de çıkarmamız gerekir. Ancak bazı durumlarda, yalnızca her olayın olasılığını toplayarak olasılıkların toplamının doğru sonucunu elde edebiliriz. Aşağıda bu durumların ne olduğunu göreceğiz.

Kısaca toplama kuralı, bir olayın veya diğerinin gerçekleşme olasılığını, yani iki olası olaydan en az birinin gerçekleşme olasılığını hesaplamak için kullanılır.

Toplama kuralı formülü

Toplama kuralı, A olayının veya B olayının meydana gelme olasılığını hesaplamak için, A olayının meydana gelme olasılığını artı B olayının meydana gelme olasılığını toplamamız ve her iki olayın aynı anda meydana gelme olasılığını çıkarmamız gerektiğini söyler. .

Toplama kuralının (veya toplama kuralının) formülü bu nedenle aşağıdaki gibidir:

toplama kuralı formülü, toplama kuralı formülü

Altın:

$P(A\cup B)$

A olayının veya B olayının olasılığıdır.
$P(A)$

A olayının gerçekleşme olasılığıdır.
$P(B)$

B olayının gerçekleşme olasılığıdır.
$P(A\cap B)$

A olayı ve B olayının meydana gelme olasılığı ortak olasılıktır.

Bu nedenle toplam kuralını kullanabilmek için iki olayın ortak olasılığının nasıl hesaplanacağını bilmeniz gerekir. Bunun nasıl yapıldığını aşağıdaki bağlantıda görebilirsiniz:

➤ Bakınız: Ortak olasılık nasıl hesaplanır?

Özel etkinlikler için örnek toplam kuralı

Konsepti anlamayı tamamlamak için toplama kuralının nasıl uygulanacağına ilişkin bir örnek görelim.

Bir kutuya 10 mavi top, 6 turuncu top ve 4 yeşil top koyuyoruz. Mavi veya turuncu bir top çekme olasılığı nedir?

Alıştırma bizden şu veya bu olayın meydana gelme olasılığını belirlememizi ister. Bu nedenle sorunu çözmek için toplama kuralı formülünü kullanmamız gerekir:

$P(A\cup B)=P(A)+P(B)-P(A\cap B)$

Bu nedenle, öncelikle Laplace kuralını kullanarak her bir olayın ayrı ayrı meydana gelme olasılığını hesaplıyoruz:

$P(\text{bola azul})=\cfrac{10}{10+6+4}=0,5$

$P(\text{bola naranja})=\cfrac{6}{10+6+4}=0,3$

Ancak bu durumda olayların her ikisi de aynı anda gerçekleşemez çünkü bunlar birbirini dışlayan iki olaydır . Yani eğer mavi bir top çekersek artık turuncu bir top çekemeyiz ve bunun tersi de geçerlidir.

Bu nedenle, her iki olayın ortak olasılığı sıfırdır ve dolayısıyla toplam kuralı formülü basitleştirilmiştir:

$P(A\cup B)=P(A)+P(B)-\cancelto{0}{P(A\cap B)}$

Yani mavi bir top veya turuncu bir top yakalama olasılığının hesaplanması şu şekildedir:

$\begin{aligned}P(\text{bola azul}\cup \text{bola naranja})&=P(\text{bola azul})+P(\text{bola azul})\\[2ex]&=0,5+0,3\\[2ex]&=0,8\end{aligned}$

Kısaca kutudan mavi veya turuncu bir top çekme olasılığı %80’dir.

Özel olmayan etkinlikler için örnek ekleme kuralı

Olaylar özel olduğunda toplama kuralının somut bir örneğini gördükten sonra, şimdi olaylar özel olmadığında bu yasanın nasıl kullanıldığını göreceğiz.

Bir parayı iki kez atarsak en az bir atışta tura gelme olasılığı nedir?

Bu durumda olaylar birbirini dışlamaz çünkü ilk atışta tura, ikinci atışta ise yazı gelebilir. Toplama kuralının formülü bu nedenle basitleştirilmemiştir ve aşağıdaki gibidir:

$P(A\cup B)=P(A)+P(B)-P(A\cap B)$

Bu nedenle, öncelikle Laplace kuralını uygulayarak yazı tura atıldığında “tura” gelme olasılığını hesaplamamız gerekir:

$P(\text{cara})=\cfrac{1}{2}=0,5$

Ek olarak, iki olay bağımsızdır, dolayısıyla iki olayın ortak olasılığını çarpım kuralını kullanarak hesaplayabiliriz:

$P(\text{cara}\cap \text{cara})=\cfrac{1}{2}\cdot \cfrac{1}{2}=0,5\cdot 0,5=0,25$

Son olarak, iki atıştan en az birinde tura gelme olasılığını bulmak için, değerleri toplama kuralı formülünde yerine koymanız ve hesaplamayı yapmanız yeterlidir:

$\begin{aligned}P(\text{cara}\cup \text{cara})&=P(\text{cara})+P(\text{cara})-P(\text{cara}\cap \text{cara})\\[2ex]&=0,5+0,5-0,25\\[2ex]&=0,75\end{aligned}$

Sonuç olarak, bir parayı iki kez attığınızda en az bir kez tura gelme olasılığı %75’tir.

yazar hakkında

Dr.benjamin anderson

Merhaba, ben Benjamin, emekli bir istatistik profesörü ve Statorials öğretmenine dönüştüm. İstatistik alanındaki kapsamlı deneyimim ve uzmanlığımla, öğrencilerimi Statorials aracılığıyla güçlendirmek için bilgilerimi paylaşmaya can atıyorum. Daha fazlasını bil