Excel'de tukey-kramer post hoc testi nasıl gerçekleştirilir

Üç veya daha fazla bağımsız grubun ortalamaları arasında istatistiksel olarak anlamlı bir fark olup olmadığını belirlemek için tek yönlü ANOVA kullanılır.

ANOVA’da kullanılan varsayımlar aşağıdaki gibidir:

Sıfır hipotezi (H ₀ ): µ ₁ = µ ₂ = µ ₃ = … = µ _k (ortalamalar her grup için eşittir)

Alternatif hipotez: (Ha): Araçlardan en az biri diğerlerinden farklıdır

ANOVA’nın p değeri anlamlılık seviyesinin altındaysa sıfır hipotezini reddedebilir ve grup ortalamalarından en az birinin diğerlerinden farklı olduğunu söylemek için yeterli kanıtımız olduğu sonucuna varabiliriz.

Ancak bu bize hangi grupların birbirinden farklı olduğunu söylemez. Bu bize basitçe tüm grup ortalamalarının eşit olmadığını söyler. Hangi grupların birbirinden farklı olduğunu tam olarak bilmek için post hoc test yapmamız gerekiyor.

En yaygın kullanılan post hoc testi, grupların her ikili kombinasyonu arasındaki ortalamayı karşılaştıran Tukey-Kramer testidir .

Aşağıdaki örnek, Excel’de Tukey-Kramer testinin nasıl gerçekleştirileceğini gösterir.

Örnek: Excel’de Tukey-Kramer testi

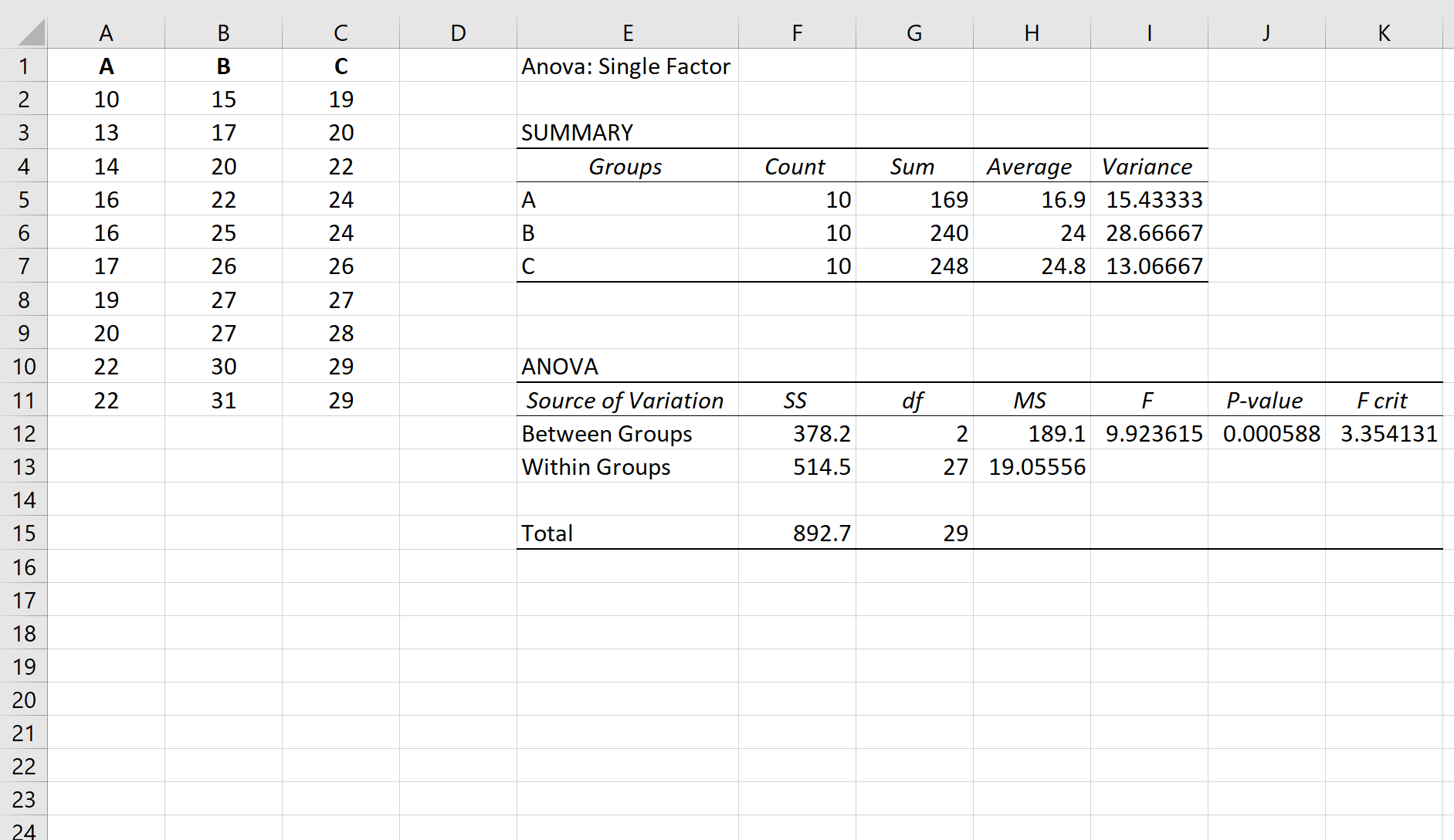
Diyelim ki üç grup üzerinde tek yönlü bir ANOVA gerçekleştiriyoruz: A, B ve C. Tek yönlü ANOVA’nın sonuçları aşağıda gösterilmektedir:

İlgili: Excel’de Tek Yönlü ANOVA Nasıl Gerçekleştirilir

ANOVA tablosunun p değeri 0,000588’dir . Bu p değeri 0,05’ten küçük olduğundan sıfır hipotezini reddedebilir ve üç grup arasındaki ortalamaların eşit olmadığı sonucuna varabiliriz.

Tam olarak hangi grup ortalamalarının farklı olduğunu belirlemek için aşağıdaki adımları kullanarak bir Tukey-Kramer post hoc testi yapabiliriz:

Adım 1: Her grup arasındaki mutlak ortalama farkı bulun.

İlk olarak, ANOVA sonucunun ilk tablosunda listelenen ortalamaları kullanarak her grup arasındaki mutlak ortalama farkı bulacağız:

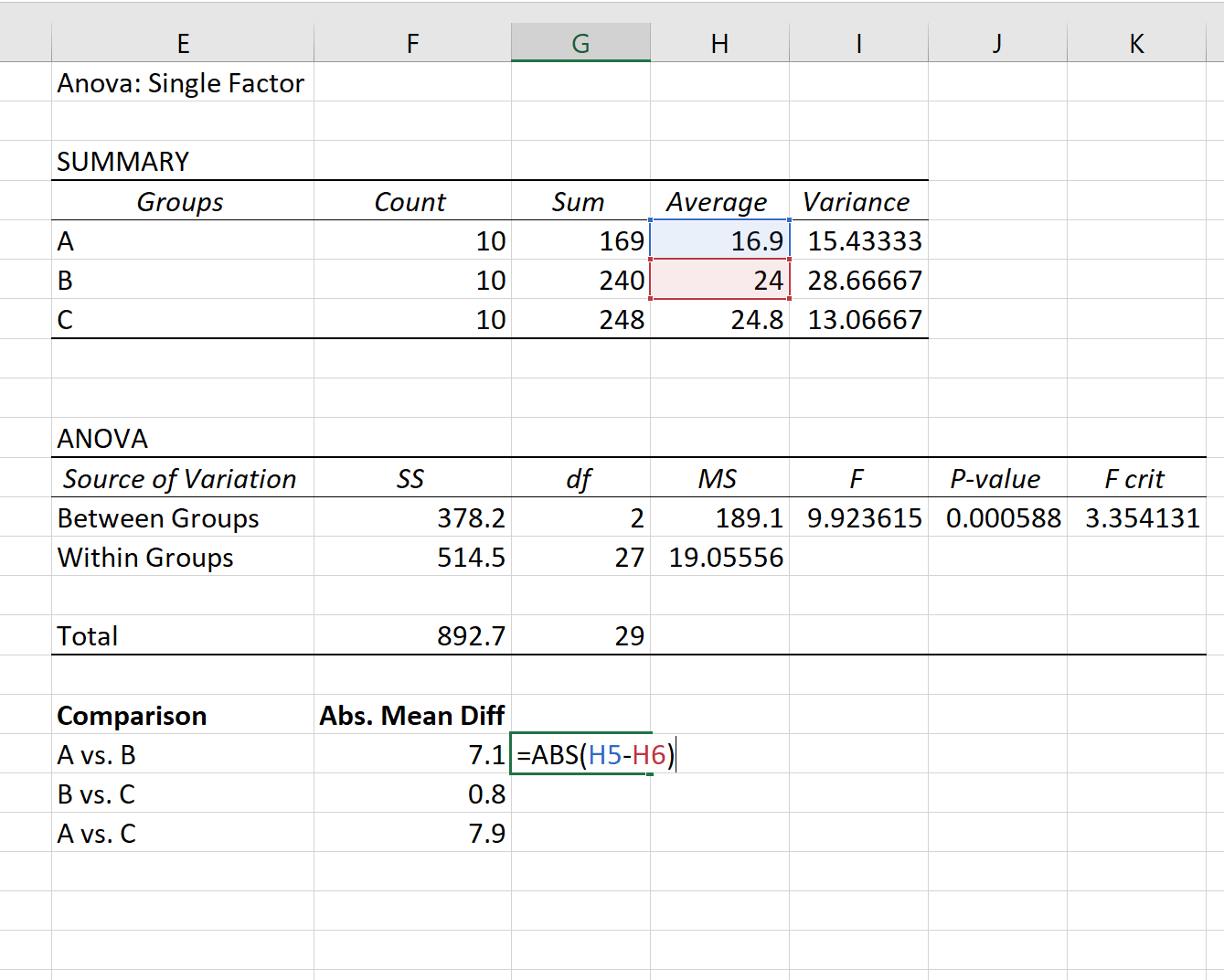
Adım 2: Q’nun kritik değerini bulun.

Daha sonra, aşağıdaki formülü kullanarak Q’nun kritik değerini bulmamız gerekiyor:

Kritik değer Q = Q*√(s ² _{gruplandırılmış} / n.)

Altın:

• Q = Öğrenci Tablosu Q aralığının değeri
• s ² _{havuzlanmış} = tüm gruplarda havuzlanmış varyans
• Olumsuz. = Belirli bir grup için örneklem büyüklüğü

Q değerini bulmak için şuna benzeyen Öğrencileştirilmiş aralık Q tablosuna başvurabilirsiniz:

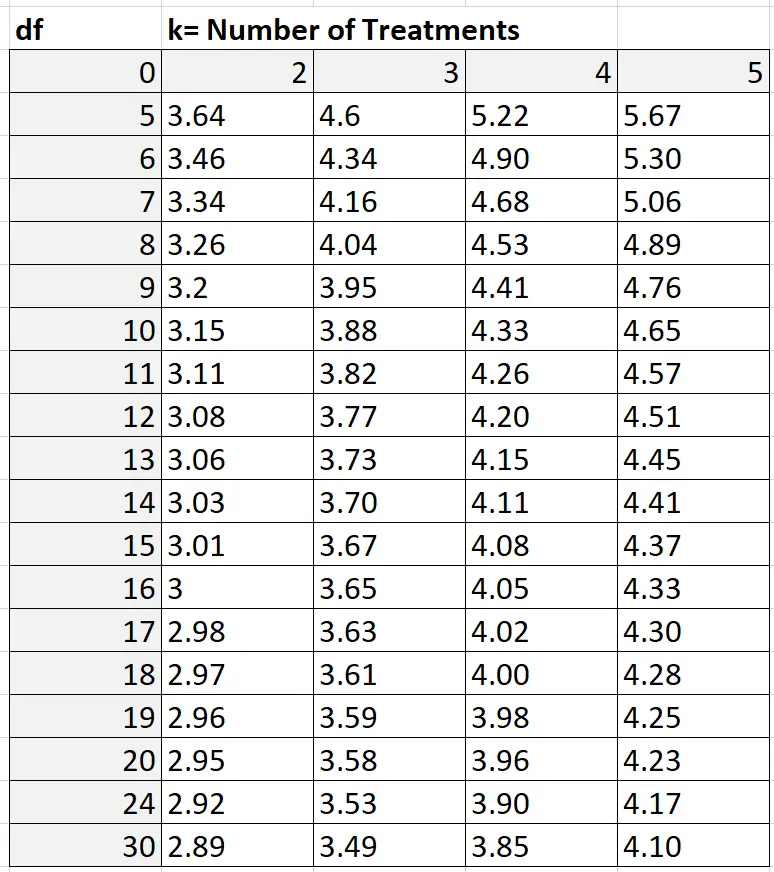
Örneğimizde k = grup sayısı yani k = 3. Serbestlik dereceleri şu şekilde hesaplanır: nk = 30 – 3 = 27. Yukarıdaki tabloda 27 gösterilmediğinden 24 gibi ihtiyatlı bir tahmin kullanabiliriz. k = 3 ve df = 24’e dayanarak Q = 3,53’ü buluruz.

Havuzlanmış varyans, grupların varyanslarının ortalaması olarak hesaplanabilir ve bu da 19.056 olarak ortaya çıkar.

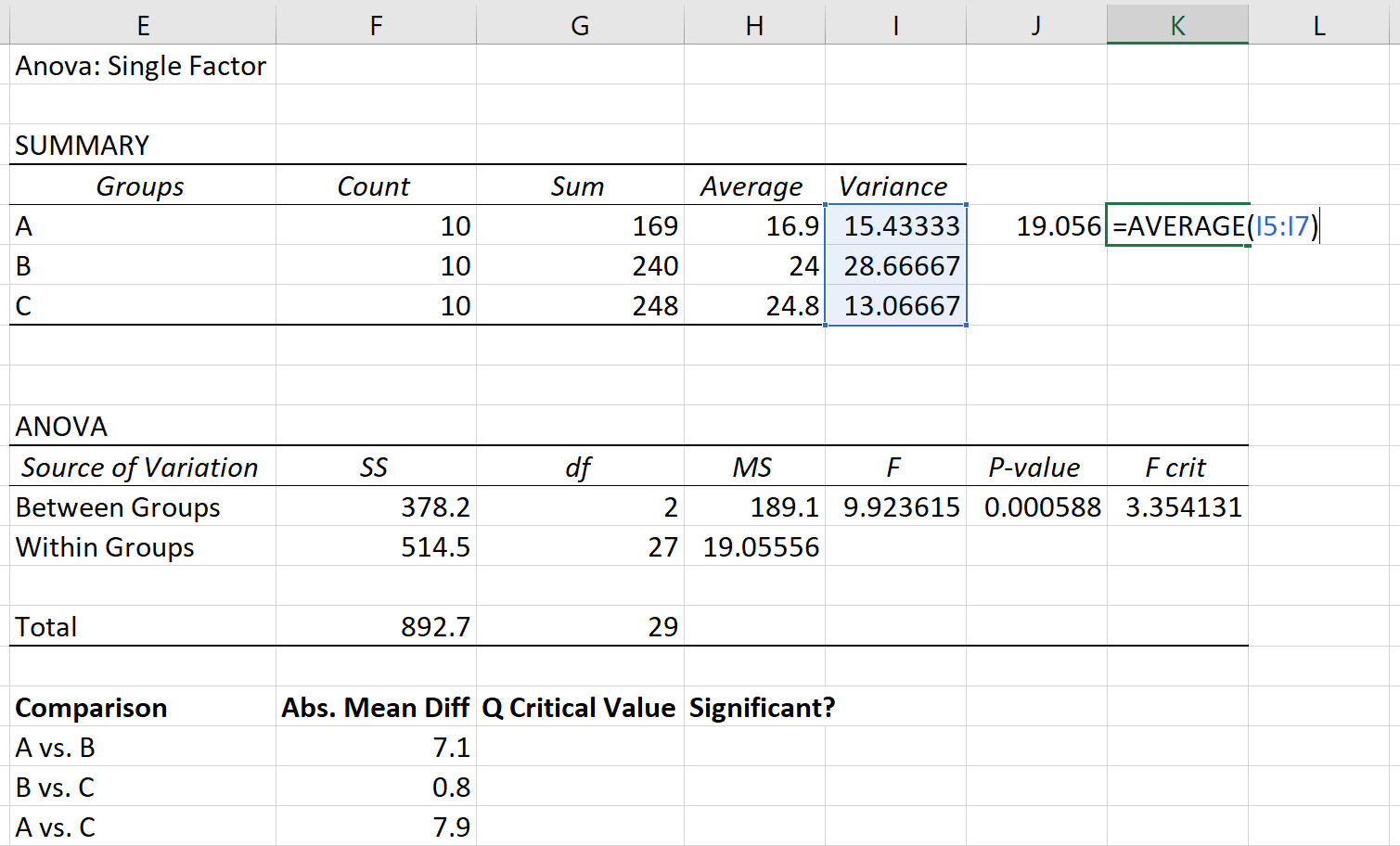
Son olarak her grubun örneklem büyüklüğü 10’dur.

Böylece kritik değerimiz Q şu şekilde hesaplanabilir:

Kritik değer Q = Q*√(s ² _{gruplandırılmış} / n.) = 3,53*√(19,056/10) = 4,87 .

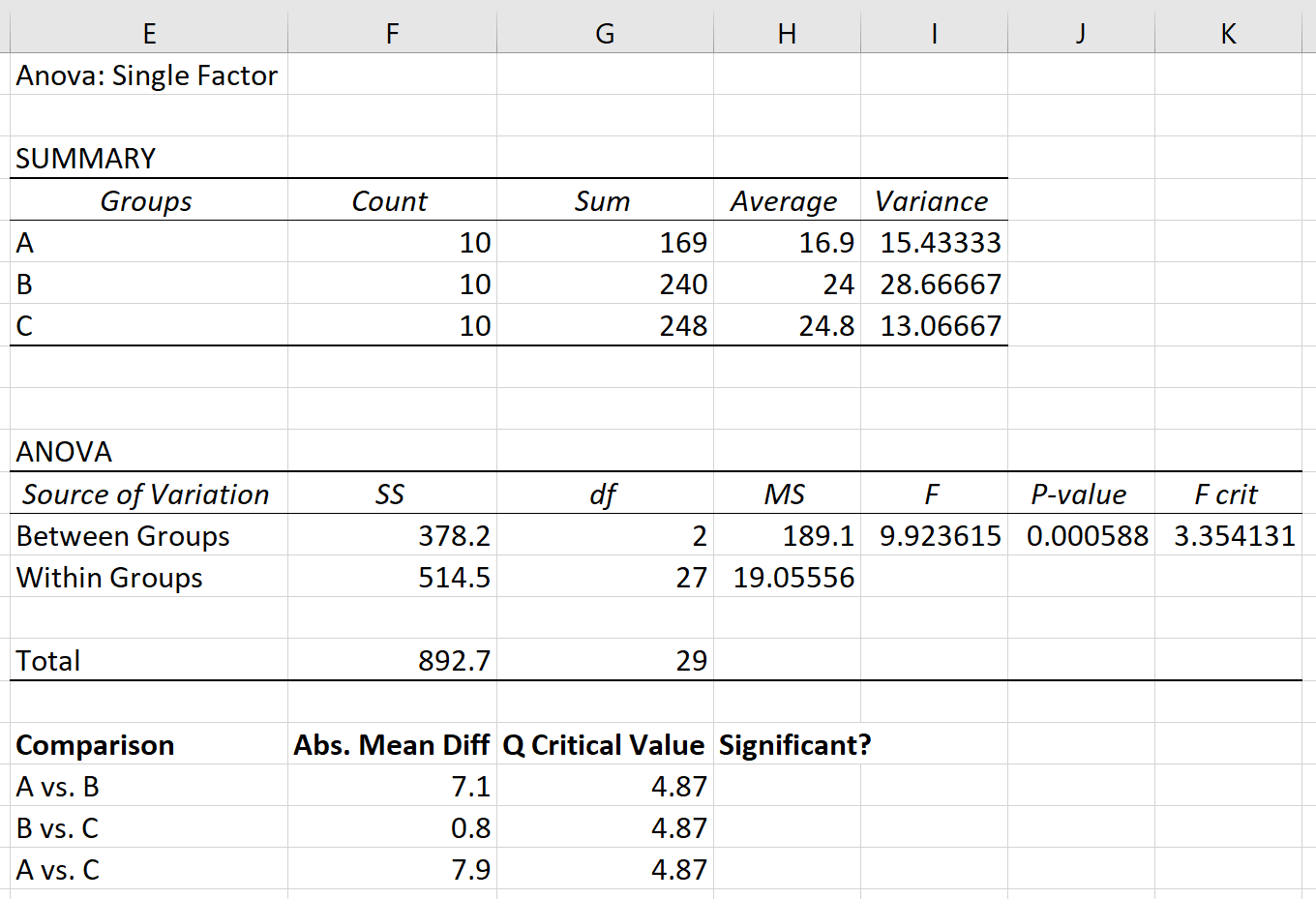
Adım 3: Hangi grup ortalamalarının farklı olduğunu belirleyin .

Son olarak, her grup arasındaki mutlak ortalama farkını kritik Q değeriyle karşılaştırabiliriz. Eğer mutlak ortalama fark, Q kritik değerinden büyükse, grup ortalamaları arasındaki fark istatistiksel olarak anlamlıdır:

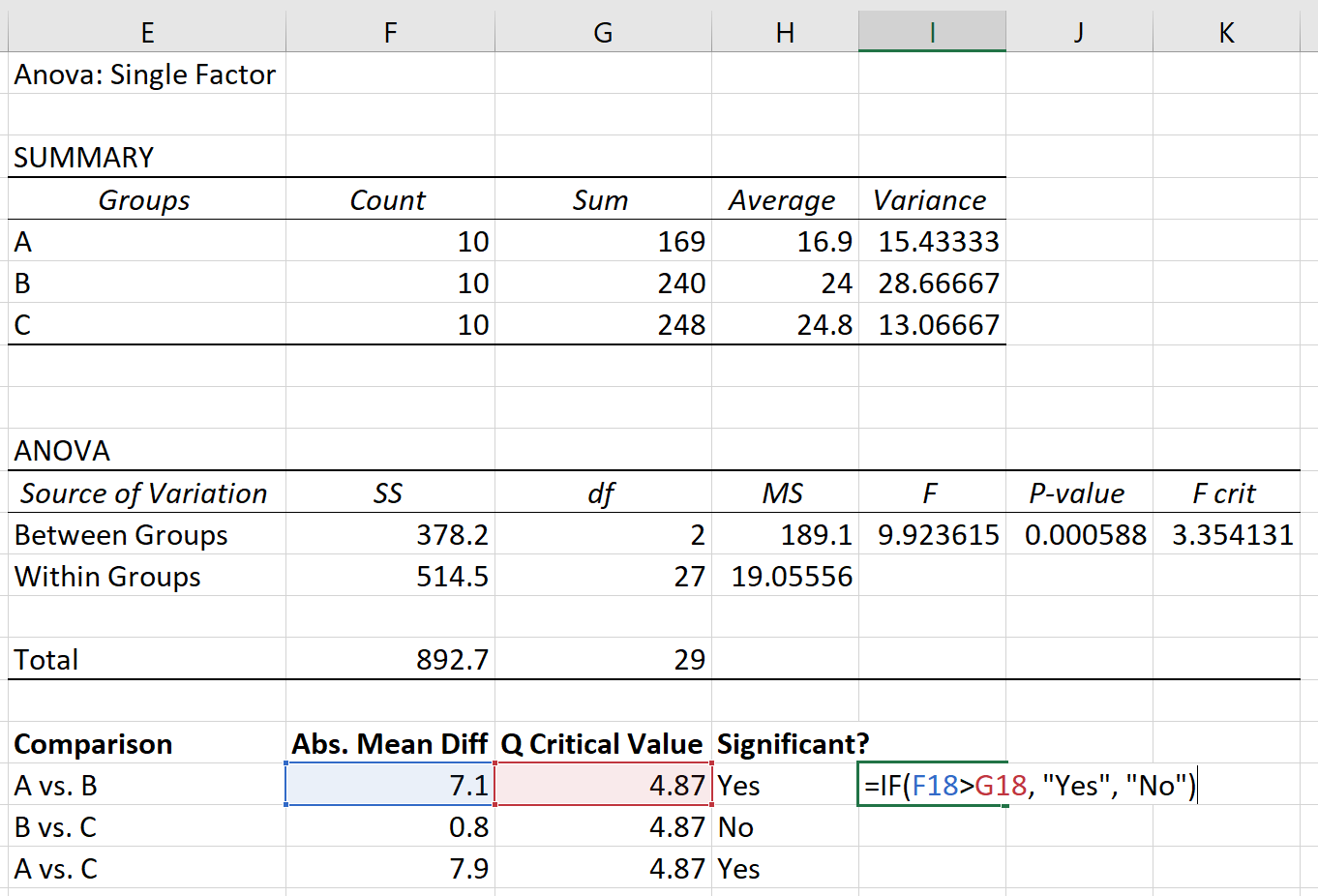
Tukey-Kramer post hoc testine dayanarak aşağıdakileri bulduk:

• A grubu ile B grubu arasındaki ortalamalar arasındaki fark istatistiksel olarak anlamlıdır.
• B grubu ile C grubu arasındaki ortalamalar arasındaki fark istatistiksel olarak anlamlı değildir .
• A grubu ile C grubu arasındaki ortalamalar arasındaki fark istatistiksel olarak anlamlıdır.

Ek kaynaklar

Excel’de Tek Yönlü ANOVA Nasıl Gerçekleştirilir
ANOVA ile Post-Hoc Testini Kullanma Kılavuzu